The power of the Sort tool lies in its ability to sort the features spatially. Once sorted spatially, efficiency of spatial or geometric operations is enhanced.
To sort features spatially (that is, by location), you must select Shape in the Field(s) parameter. Selecting the shape field enables the Spatial Sort Method parameter with five drop-down options which lets you set the sorting algorithm. The options are UL, UR, LL, LR, and PEANO.
Spatial sorting using UL, UR, LL, LR
The first four options are abbreviations of the starting point for sorting; for example, UR is for upper right and LR is for lower left. These options scan the features like a plotter or a printer. If the UR option is chosen, scanning begins at the upper right corner, selecting the top feature first. Coming from the top down, if two or more features are at the same horizontal line, then they are ordered from right to left. The scanning continues downward and leftward until it reaches the opposite (lower left in this case) corner. Features are sorted in the same order (or opposite order if DESCENDING is selected) as they are scanned or visited.
The UR sorting option can be demonstrated in an uncomplicated way by taking a uniformly distributed set of points as input.
The numbers in the above diagram represents sorted sequence for UR option. The order of features is reversed if the LL option is selected.
Here is a simple example on how upper and right work together.
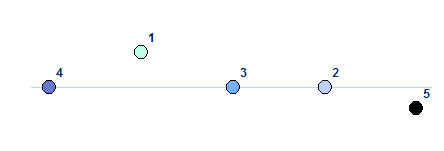
Note that U gets priority over R. R is taken into considerations only when some features are at the same horizontal level.
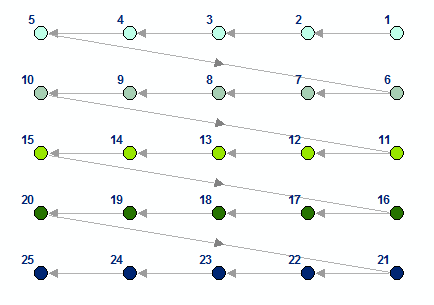
Spatial sorting by PEANO
The PEANO option uses the Peano curve algorithm. The algorithm visits all the locations of a smaller neighborhood first before moving onto the next neighborhood. Thus, nearby locations are closer along the curve (or path). Instead of searching the whole extent—it searches smaller neighborhoods one by one and after finishing a larger area (of say, 5 to 8 smaller neighborhoods)—it moves to another larger area and restarts sorting from a smaller neighborhood within that bigger area.

In the above diagram, the scanning sequence is shown by arrows. Each of the four rectangular neighborhoods are scanned separately. If the area were larger, the search would continue for another set of neighborhoods, and so on. If the points were more dense, a much smaller neighborhood would have been searched.
The advantages of a space-filling curve algorithm include the following: it is fast, it does not require calculating distances between locations, and it is parallelizable. Applications of such an algorithm include the traveling salesman problem, building a routing system, and controlling a pen-plotter for the drawing of maps.