Available with Geostatistical Analyst license.
Quantile-quantile (QQ) plots are graphs on which quantiles from two distributions are plotted relative to each other.
How the Normal QQ plot is constructed
First, the data values are ordered and cumulative distribution values are calculated as (i– 0.5)/n for the ith ordered value out of n total values (this gives the proportion of the data that falls below a certain value). A cumulative distribution graph is produced by plotting the ordered data versus the cumulative distribution values (graph on the top left in the figure below). The same process is done for a standard normal distribution (a Gaussian distribution with a mean of 0 and a standard deviation of 1, shown in the graph on the top right of the figure below). Once these two cumulative distribution graphs have been generated, data values corresponding to specific quantiles are paired and plotted in a QQ plot (bottom graph in the figure below).
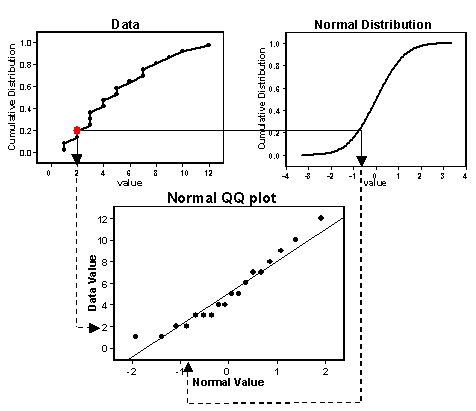
How the general QQ plot is constructed
General QQ plots are used to assess the similarity of the distributions of two datasets. These plots are created following a similar procedure as described for the Normal QQ plot, but instead of using a standard normal distribution as the second dataset, any dataset can be used. If the two datasets have identical distributions, points in the general QQ plot will fall on a straight (45-degree) line.

Examining data distributions using QQ plots
Points on the Normal QQ plot provide an indication of univariate normality of the dataset. If the data is normally distributed, the points will fall on the 45-degree reference line. If the data is not normally distributed, the points will deviate from the reference line.
In the diagram below, the quantile values of the standard normal distribution are plotted on the x-axis in the Normal QQ plot, and the corresponding quantile values of the dataset are plotted on the y-axis. You can see that the points fall close to the 45-degree reference line. The main departure from this line occurs at high values of ozone concentration.
The Normal QQ Plot tool allows you to select the points that do not fall close to the reference line. The location of the selected points are then highlighted in the ArcMap data view. As seen below, they are concentrated around the San Francisco Bay area (points shaded in pink on the map below).
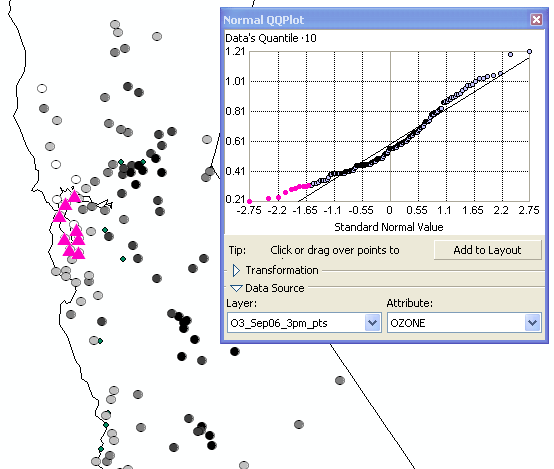
An example of using data transformations
A Normal QQ plot of an example dataset is presented here:

Notice how the points stray from the straight line.
However, as can be seen in the figure below, when a log transformation is applied to the dataset, the points lie closer to the 45-degree reference line.

Box-Cox and arcsine transformations can also be applied to the data within the Normal QQ Plot tool to assess their effect on the normality of the distribution.