Available with Spatial Analyst license.
Different raster datasets do not need to be stored using the same cell resolution. But when you are processing between multiple datasets, the cell resolution, like the registration, ideally should be the same. When multiple raster datasets are input into any ArcGIS Spatial Analyst extension tool and their resolutions are different, one or more of the input datasets will be automatically resampled to the coarsest resolution of the input datasets.
In the default case, the nearest neighbor assignment resampling technique is used. This is because it is applicable to both discrete and continuous value types, while the other resampling types—bilinear interpolation and cubic convolution—are only applicable to continuous data. A resampling technique is necessary because rarely do the centers of the input cells align with the transformed cell centers of the desired resolution. The bilinear and cubic techniques can be applied using the Resample tool as a pre-processing step before combining rasters of different resolutions.
The resolution of the default resampling can be controlled with the Cell size environment parameter, where you can specify that the tool use either the minimum resolution of the input rasters or a specific cell size that you define.
In the image below, the cell size that was set in the analysis environment is coarser than the cell size of the input raster to the tool. On execution, the input raster will first be resampled to the coarser resolution, then the tool is applied.

When performing analysis, make sure you are asking appropriate questions of the cell size. For example, it is unlikely you will study mouse movement when the cell size is 5 kilometers. Five-kilometer cells might be more applicable when studying the effects of global warming over the earth.
Resampling
To find the value each cell should receive on the resampled output raster, the center of each cell in the output must be mapped to the original input coordinate system. Each cell center coordinate is transformed backward to identify the location of the point on the original input raster. Once the input location is identified, a value can be assigned to the output location based on the nearby cells in the input. It is rare that an output cell center will align exactly with any cell center of the input raster. Therefore, techniques have been developed to determine the output value depending on where the point falls relative to the center of cells of the input raster and the values associated with these cells. The three techniques for determining output values are nearest neighbor assignment, bilinear interpolation, and cubic convolution. Each of these techniques assigns values to the output differently. Thus, the values assigned to the cells of an output raster may differ according to the technique used.
Nearest neighbor assignment
Nearest neighbor assignment is the resampling technique of choice for discrete (categorical) data since it does not alter the value of the input cells. Once the location of the cell's center on the output raster dataset is located on the input raster, nearest neighbor assignment will determine the location of the closest cell center on the input raster and assign the value of that cell to the cell on the output raster.
The nearest neighbor assignment does not change any of the values of cells from the input raster dataset. The value 2 in the input raster will always be the value 2 in the output raster; it will never be 2.2 or 2.3. Since the output cell values remain the same, nearest neighbor assignment should be used for nominal or ordinal data, where each value represents a class, member, or classification (categorical data such as a land-use, soil, or forest type).
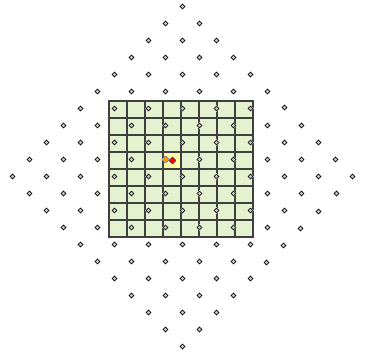
Consider an output raster created from an input raster that is rotated 45° in an operation and thus will be resampled. For each output cell, a value needs to be derived from the input raster. In the illustration below, the cell centers of the input raster are the gray points. The output cells are shaded in green. The cell being processed is shaded in yellow. In the nearest neighbor assignment, the cell center from the input raster that is closest (orange point) to the processing cell center (red point) is identified and assigned as the output value for the processing cell (shaded yellow). This process is repeated for each cell in the output raster.
Bilinear interpolation
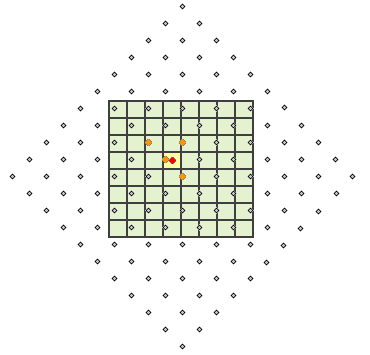
Bilinear interpolation uses the value of the four nearest input cell centers to determine the value on the output raster. The new value for the output cell is a weighted average of these four values, adjusted to account for their distance from the center of the output cell. This interpolation method results in a smoother-looking surface than can be obtained using nearest neighbor.
In the following illustration, as in the previous one for nearest neighbor interpolation, the cell centers of the input raster are in gray points, the output cells are shaded in green, and the cell being processed is shaded in yellow. For bilinear interpolation, the four input cell centers (orange points) nearest to the processing cell center (red point) are identified, the weighted average is calculated, and the resulting value is assigned as the output value for the processing cell (shaded yellow).
Since the values for the output cells are calculated according to the relative position and the value of the input cells, bilinear interpolation is preferred for data where the location from a known point or phenomenon determines the value assigned to the cell (that is, continuous surfaces). Elevation, slope, intensity of noise from an airport, and salinity of the groundwater near an estuary are all phenomena represented as continuous surfaces and are most appropriately resampled using bilinear interpolation.
Cubic convolution
Cubic convolution is similar to bilinear interpolation except that the weighted average is calculated from the 16 nearest input cell centers and their values.
The following illustration demonstrates how the output value is calculated for cubic convolution. The 16 input cell centers (orange points) nearest to the processing cell center (red point) are identified, the weighted average is calculated, and the resulting value is assigned as the output value for the processing cell (shaded yellow).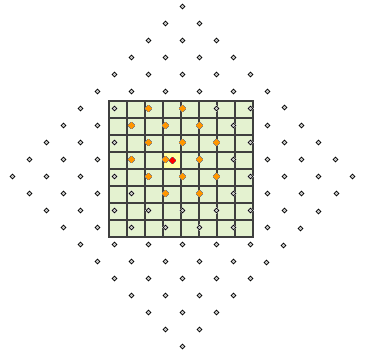
Cubic convolution will have a tendency to sharpen the edges of the data more than bilinear interpolation since more cells are involved in the calculation of the output value.
Resampling and data types
Bilinear interpolation or cubic convolution should not be used on categorical data since the categories will not be maintained in the output raster dataset. However, all three techniques can be applied to continuous data, with nearest neighbor producing a blocky output, bilinear interpolation producing smoother results, and cubic convolution producing the sharpest.