Available with Spatial Analyst license.
For the path distance tools, there are several parameters that allow you to control the horizontal and vertical friction factors.
Before reading this section, be sure that you first have some understanding of the basics of path distance analysis and how the tools work.
Horizontal factors
The horizontal factors
The horizontal factors (HFs) influence the total cost, or difficulty, of moving from one cell to another by accounting for any horizontal frictional elements encountered.
To calculate the total HF for traveling between cells, the HF for the segment of the link from the center of the processing cell to the edge of the To cell and for the segment of the link from the edge of the To cell to its center must be determined.
Determining the horizontal cost for each link is a two-step process:
- First, the prevailing horizontal direction must be established. A horizontal direction is defined in degrees, with 0 being above, or north, of the processing cell and the values increasing clockwise, creating a circle and returning to itself at 360 degrees.
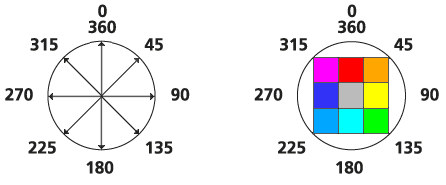
The horizontal direction is defined by a value assigned to each cell location on the input horizontal factor raster. It often identifies the direction with the lowest horizontal cost of movement with respect to the processing cell, but this does not necessarily have to be the case.
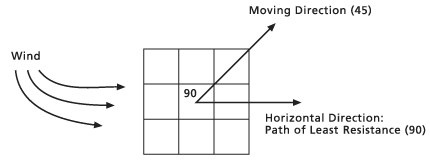
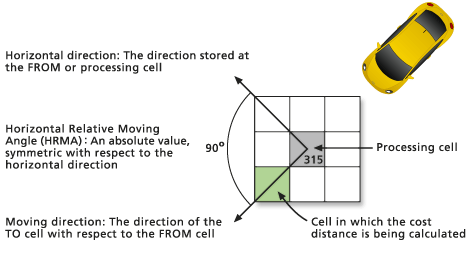
- Once the horizontal direction has been defined, the horizontal factor used in calculating the total cost of moving along the segment must be determined. First, the position of the to cell relative to the horizontal direction must be ascertained. The direction of the to cell relative to the prevailing horizontal direction at the from cell is the horizontal moving direction, or just the moving direction. The number of degrees or angle of the to cell from the horizontal direction as defined by the horizontal factor raster is the horizontal relative moving angle (HRMA).
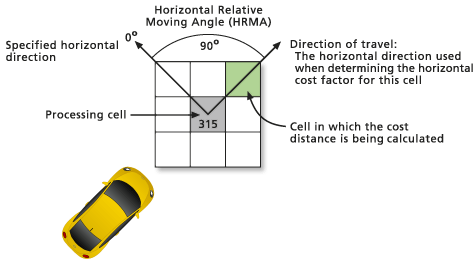
The number of degrees from the established horizontal direction, not which side of the established direction, is of relevance.
Once the HRMA has been determined, a graph is used to identify the actual horizontal factor. The HF is on the y-axis, and the HRMA is on the x-axis.
In the example above, if the cell whose horizontal factor you are calculating has an HRMA of 90 degrees from the horizontal direction as defined by the processing cell on the input horizontal factor raster, the horizontal factor cost will be 1.61.
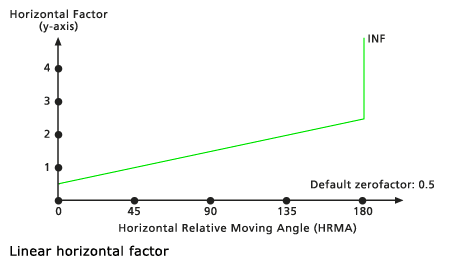
The HRMA values can range from -180 to 180 degrees. However, on the horizontal factor graph, the values on the x-axis are from 0 to 180 because the graph is assumed to be symmetrical (mirrored) around the horizontal factor axis; that is, 180 degrees is opposite the direction specified by the horizontal direction raster, and 90 degrees is to the right and left of the processing cell. INF means the line goes to infinity.
This same process is performed for the segment starting at the edge of the To cell and ending at its center. The moving direction remains the same, but the horizontal direction that will be used for the calculations is the prevailing horizontal direction at the To cell. Dividing the travel link between two cells into two segments (half the segment being in the From cell and the other half in the To cell) will give a more accurate horizontal factor since half the distance from the From cell to the To cell encounters the cost associated with the From cell; the remainder of the distance will be in the adjoining cell, which has a different horizontal resistance. In the path distance formula, each segment's horizontal factor is multiplied by its respective cost factors determined from the cost raster.
Horizontal factor keywords
The horizontal factor graph that will be used to determine the horizontal factor can be defined by either choosing an existing graph from the graphs provided with the software or creating a custom graph from an ASCII file. The existing graphs provided with the software are the following:
- Binary
When the HRMA is less than the cutting angle, the HF for moving through the section of the cell is set to the value associated with the Zero factor. If the HRMA is greater than the cutting angle, the HF for the section is set to infinity. The default cutting angle is 45 degrees. The default zero factor is 1.0.
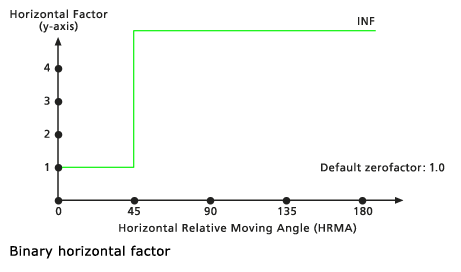
Default Binary horizontal factor graph - Forward
If an HRMA is less than 45 degrees for a section of travel, the HF is set to the value associated with the Zero factor. When the HRMA is larger than or equal to 45 degrees and less than 90 degrees, the HF is set to the Side value. If no side value is specified, the default side value is 1. If the HRMA is equal to or greater than 90 degrees, the HF is set to infinity. The default zero factor is 0.5.
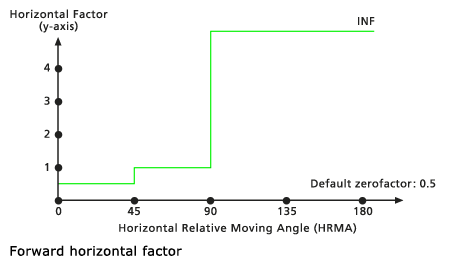
Default Forward horizontal factor graph - Linear
The HFs are determined by a straight line in the HRMA-HF coordinate system. The line intercepts the y-axis, equitable to the HF factor, at the value associated with the Zero factor. The slope of the line can be specified using the Slope modifier. If no slope is identified, the default is 0.5/45 or 1/90 (specified as 0.01111). The default cutting angle is 181 degrees, which equates to no cutting. The default zero factor is 0.5.

Default Linear horizontal factor graph - Inverse linear
The HFs are determined by the inverse values from a straight line in the HRMA-HF coordinate system. The line intercepts the y-axis, equitable to the HF factor, at the value associated with the Zero factor. The slope of the line can be specified with the Slope modifier. If no slope is identified, the default is -2/180 or -1/90 (specified as 0.01111). The default cutting angle is 181 degrees, which equates to no cutting. The default zero factor is 2.0.
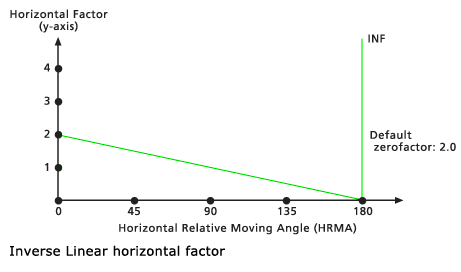
Default Inverse Linear horizontal factor graph - Table
A graph can be defined with an ASCII file created in any text editor. The file consists of two columns of values on each line. The first value identifies the HRMA, which is expressed in degrees, and the second, the HF. Each line in the file specifies a point on the graph. Two consecutive points define a line segment in the HRMA-HF coordinate system. The HRMA angles must be entered in ascending order. The HF factor for any HRMA angle less than the first (lowest) input value or larger than the last (largest) input value will be set to infinity. An infinite HF is represented by -1 in the ASCII file. A sample horizontal factor ASCII table follows:
0 1.40 10 2.43 20 2.30 30 3.44 40 1.25 50 1.02 60 0.90 70 0.86 80 0.25 90 0.78 100 1.49 110 2.35 120 3.32 130 2.39 140 3.18 150 2.13 160 1.89 170 1.20 180 2.034
Horizontal factor modifiers
Several of the HRMA keyword parameters have modifiers that can be specified to achieve various desired results. The slope of the line in the Linear and Inverse linear functions, the side values for the Forward function, and the zero factor can alter the y-axis intercept for the input functions, and the cut angle for any of the HRMA functions can be controlled. Do not be concerned if you are unfamiliar with the effects of the modifiers at this point. Just be aware that you are able to further control the HRMA graphs to meet your needs.
- Zero factor
This factor will be used to position the y-intercept of the specified function. It can be used in conjunction with all horizontal factor functions.
- Cut angle
Establishes the HRMA degree threshold beyond which the HFs are set to infinity. Cut angle can be used on any of the specified horizontal factor keywords except Forward. That function, by definition, establishes its own cut angles.
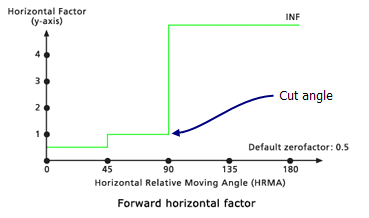
Cut angle horizontal factor modifier example - Slope
Identifies the slope of the straight lines in the HRMA–HF coordinate system for the Linear and Inverse linear keywords. Slope is specified as the rise over the run (for example, a 30-degree slope is 1/30, specified as 0.03333). See the Linear HRMA diagram for an example of a line with a slope of 1/90.
- Side value
Identifies the HF value that will be assigned for HRMAs that are equal to or less than 45 degrees and less than 90 degrees when the Forward horizontal factor keyword's used. Consult the Forward HRMA diagram, which has a side value of 1.
- Table name
Identifies the ASCII file that should be used for the Table option.
Vertical factors
The vertical factors
The vertical factors (VFs) determine the difficulty of moving from one cell to another, while accounting for the vertical elements that may affect the movement.
Determining the VF encountered when traveling from one cell to another is similar to determining the horizontal factor, except it is not broken into two segments as when calculating the HF. This is because there is only one slope between the two cell centers; hence, there is only one vertical relative moving angle (VRMA).
To determine the VF for moving from one cell to the next, the slope between the From cell and the To cell is calculated from the values defined in the input vertical factor raster. The resulting slope is the VRMA, which is plotted on the vertical factor graph to identify the value used for the vertical factor in the path distance calculations for the cell-to-cell movement. This vertical factor establishes the vertical factor from the center of the starting cell to the center of the destination cell. The larger the vertical factor, the more difficult the movement.
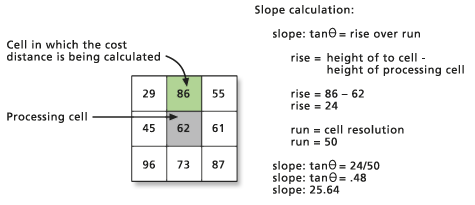
The vertical relative moving angle is the angle of slope from the From cell to the To cell. The slope is calculated using the Pythagorean theorem formula of rise/run. The base of the triangle necessary for determining the slope is derived from the cell size. The height is established by subtracting the From cell value from the To cell value. The resultant angle is the VRMA.
The VRMA is specified in degrees. The range of values for the VRMA is -90 to +90 degrees, compensating for both positive and negative slopes. The VRMA value is then plotted on the specified vertical factor graph to obtain the vertical factor that will be used in the calculations that determine the cost to reach the To cell. The resolution of the VRMAs is 0.25 degrees.
For an example, the following shows the relationship of the VF and the VRMA for a Linear type graph:

Vertical factor keywords
Defining the vertical factor graph that will be used when determining the VF involves the same steps as defining the horizontal factor graph. The graph can be selected from a list of graphs provided with the software, or you can create a custom graph with an ASCII file. The vertical factor graphs provided with with the software include the following:
- Binary
When the VRMA is larger than the low-cutting angle and smaller than the high-cutting angle, the VF for moving between the two cells is set to the value associated with the zero factor. If the VRMA is greater than the cutting angle, the VF is set to infinity. The default cutting angle is 30 degrees if none is specified.
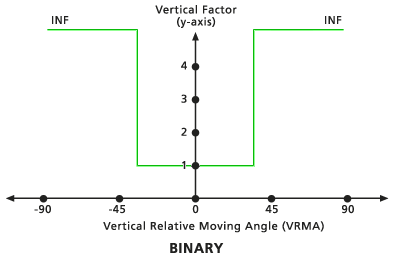
Default Binary vertical factor graph - Linear
The VFs are determined by a straight line in the VRMA-VF coordinate system. The line intercepts the y-axis, equitable to the VF factor, at the value associated with the zero factor. The slope of the line can be specified using the Slope modifier. If no slope is identified, the default is 1/90 (specified as 0.01111). The default low-cutting angle is -90 degrees, and the default high-cutting angle is 90 degrees.
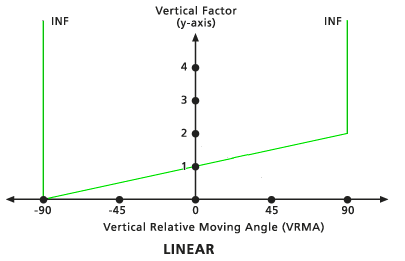
Default Linear vertical factor graph - Inverse linear
The VFs are determined by the inverse values from a straight line in the VRMA-VF coordinate system. The line intercepts the y-axis, equitable to the VF factor, the value associated with the zero factor. The slope of the line can be identified if specified with the Slope modifier. If no slope is identified, the default is -1/45 (specified as 0.02222). The default low-cutting angle is -45 degrees, and the default high-cutting angle is 45.
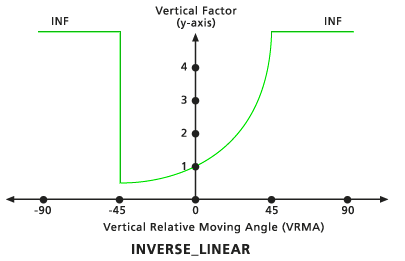
Default Inverse Linear vertical factor graph - Symmetric linear
This vertical factor is composed of two linear functions relative to the VRMAs that are symmetrical to the VF (y) axis. Both lines intercept the y-axis at the VF value associated with the zero factor. The slope of the lines is defined as a single slope relative to the positive VRMA using the Slope vertical factor modifier, which mirrors the negative VRMAs. The default slope is 1/90 (specified as 0.01111). The default low-cutting angle is -90, and the default high-cutting angle is 90.
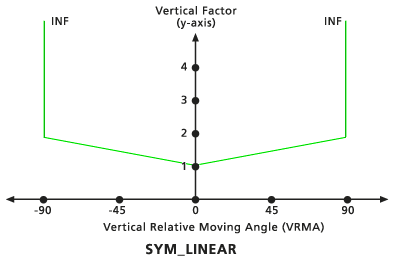
Default Symmetric Linear vertical factor graph - Symmetric inverse linear
This vertical factor is the of the Symmetric linear vertical factor keyword. It is composed of two inverse linear functions relative to the VRMAs, which are symmetrical to the VF (y) axis. Both lines intercept the y-axis at the VF of 1. The slope of the lines is defined as a single slope relative to the positive VRMA using the Slope vertical factor modifier, which mirrors the negative VRMAs. The default slope is -1/45 (specified as 0.02222). The default low-cutting angle is -45, and the default high-cutting angle is 45.
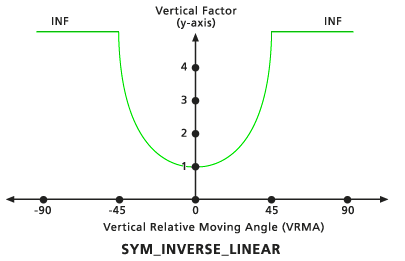
Default Symmetric Inverse Linear vertical factor graph - Cos
The VF is determined by the cosine function of the VRMA. The default low-cutting angle is -90 degrees, and the default high-cutting angle is 90 degrees. The default Cos power is 1.0.
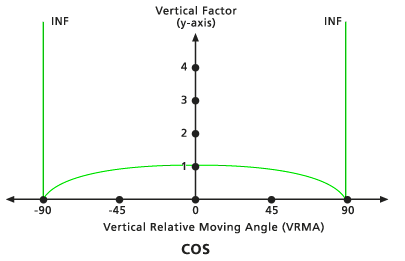
Default Cosine vertical factor graph—Default value (1.0) - Sec
The VF is determined by the secant function of the VRMA. The default low-cutting angle is -90 degrees, and the default high-cutting angle is 90 degrees. The default Sec power is 1.0.
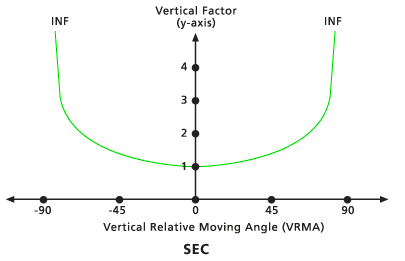
Default Secant vertical factor graph - Cos - Sec
When the VRMA is a negative degree value, the VF is determined by the cosine function of the VRMA. If the VRMA is a positive degree value, the VF is determined by the secant function of the VRMA. The default low-cutting angle is -90 degrees, and the default high-cutting angle is 90 degrees. The default Cos power and Cos power are both 1.0.
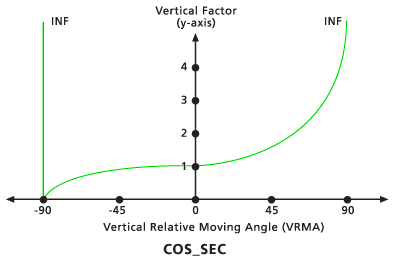
Default Cosecant vertical factor graph - Sec - Cos
When the VRMA is a negative degree value, the VF is determined by the secant function of the VRMA. If the VRMA is a positive degree value, the VF is determined by the cosine function of the VRMA. The default low-cutting angle is -90 degrees, and the default high-cutting angle is 90 degrees. The default Cos power and Cos power are both 1.0.
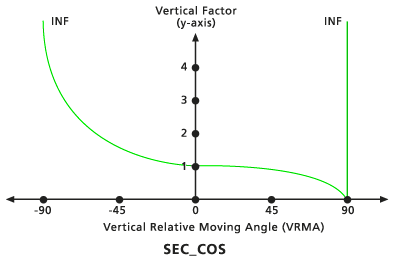
Default Secant-cosine vertical factor graph - Table
The table is an ASCII file with two columns on each line. It is similar to the Table option of the horizontal factor graph.
The first column identifies the VRMA in degrees, and the second, the VF. Each line specifies a point. Two consecutive points produce a line segment in the VRMA-VF coordinate system. The angles must be input in ascending order and range from -90 to 90. The VF factor for any VRMA angle less than the first (lowest) input value or larger than the final (largest) input will be set to infinity. An infinite VF is represented by -1 in the ASCII table.
Sample vertical factor ASCII table:
-90 -1 -80 -1 -70 2.099409721 -60 0.060064462 -50 0.009064613 -40 0.00263818 -30 0.001055449 -20 0.000500142 -10 0.00025934 0 0.000198541 10 0.000368021 20 0.000709735 30 0.001497754 40 0.003743755 50 0.012863298 60 0.085235529 70 2.979204206 80 -1 90 -1
Vertical factor modifiers
As with an HRMA graph, the character of the VRMA graph can be further controlled by modifiers that allow refinement of the vertical factors. There may be a threshold angle such that if the VRMA exceeds this angle, the cost is so great that it becomes a barrier to travel. This threshold is referred to as the cut angle. The VF is assigned to infinity when the VRMA exceeds this value.
The vertical factor graph will have both lower and upper cut angles, in contrast to the horizontal factor graph, which will only have a single cut angle.
Cut angles can be specified for each of the functions, the trigonometric curves can be raised by a power, the zero factor can alter the y-axis intercept for the non-trigonometric functions, and the slope of the line in the linear functions can be defined.
- Zero factor
Establishes the vertical factor used when the VRMA is zero. This factor positions the y-intercept of the specified function.
- Low cut angle
The VRMA degree defining the lower threshold, below which (less than) the VFs are set to infinity, regardless of the specified vertical factor keywords.
- High cut angle
The VRMA degree defining the upper threshold, beyond which (larger than) the VFs are set to infinity, regardless of the specified vertical factor keywords.
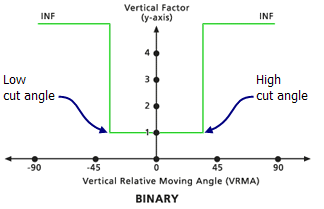
Low and High cut angle vertical factor modifiers example - Slope
Identifies the slope of the straight lines in the VRMA-VF coordinate system for the Linear, Inverse linear, Symmetric linear, and Symmetric inverse linear keywords. Slope is specified as the rise/run (for example, a 30-degree slope is 1/30, specified as 0.03333). Refer to the Linear VRMA diagram for an example of a linear function with a slope of 1/90.
- Power
The power to which the values will be raised.
- Cos power
The power to which the nonnegative values in the Sec-Cos VRMA function and the negative values in the Cos-Sec VRMA function will be raised. The VF is determined by the following:
VF = cos(VRMA)power - Sec power
The power to which the nonnegative values in the Cos-Sec VRMA function and the negative values in the Sec-Cos VRMA function will be raised. The VF is determined by the following:
VF = sec(VRMA)power - Table name
Identifies the name of the ASCII file that will be used with the Table vertical factor keyword.