Mit der Geostatistical Analyst-Lizenz verfügbar.
When you have multiple datasets and you want to use cokriging, you need to develop models for cross-covariance. Because you have multiple datasets, you keep track of the variables with subscripts, with Zk(sj ) indicating a random variable for the kth data type at location si . The cross-covariance function between the kth data type and the mth data type is then defined to be
C km (si,sj) = cov(Zk(si), Zm(sj)).Here is a subtle and often confusing fact: C km (si ,sj ) can be asymmetric: C km (si ,sj ) ≠ C mk (si ,sj ) (notice the switch in the subscripts). To see why, look at the following example. Suppose you have data arranged in one dimension, along a line, such as the following:
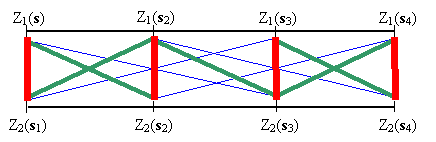
The variables for type 1 and 2 are regularly spaced along the line, with the thick red line indicating highest cross-covariance, the green line less cross-covariance, and the thin blue line the least cross-covariance, with no line indicating 0 cross-covariance. This figure shows that Z1(si ) and Z2(sj ) have the highest cross-covariance when si = sj , and the cross-covariance decreases as si and sj get farther apart. In this example, C km (si ,sj ) = C mk (si ,sj ). However, the cross-covariance can be "shifted":
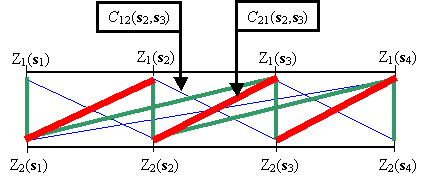
Notice that C12(s2,s3) now has the minimum cross-covariance (thin blue line) while C21(s2,s3) has the maximum cross-covariance (thick red line), so here C km (si ,sj ) ≠ C mk (si ,sj ). Relative to Z1, the cross-covariances of Z2 have been shifted -1 unit. In two dimensions, Geostatistical Analyst will estimate any shift in the cross-covariance between the two datasets if you click the shift parameters.
The empirical cross-covariances are computed as follows:
Average [ (z1(si) -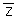 
1) (z2(sj) - 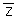2)]
where Zk
(si
) is the measured value for the kth data set at location si
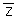,k is the mean for the kth dataset, and the average is taken for all si
and sj
separated by a certain distance and angle. As for the semivariograms, Geostatistical Analyst shows both the empirical and fitted models for cross-covariance.
Choosing different cross-covariance models, using compound cross-covariance models, and choosing anisotropy will all cause the theoretical model to change. You can make a preliminary choice of model by seeing how well it fits the empirical values. Changing the lag size and the number of lags and adding shifts will change the empirical cross-covariance surface, which will cause a corresponding change in the theoretical model. Geostatistical Analyst computes default values, but you should feel free to try different values and use validation and cross-validation to choose the best model.
- Learn about covariation among multiple datasets
- Learn how to change the lag size
- Learn about selecting a model
- Learn about model anisotropy