Mit der Spatial Analyst-Lizenz verfügbar.
Mithilfe der Erweiterung "ArcGIS Spatial Analyst" können Sie eine Klassifizierung erstellen, indem Sie Raster-Zellen in Klassen oder Cluster gruppieren. Eine Klasse ist normalerweise eine bekannte Kategorie, z. B. Wälder, Wohngebiete oder Gewässer, während ein Cluster eine Gruppierung von Zellen auf Grundlage der Statistik ihrer Attribute ist. Eine Signatur ist eine Teilmenge von Zellen, die für eine Klasse oder einen Cluster repräsentativ sind. Die Statistiken von Signaturen werden in einer Signaturdatei gespeichert, mit der alle Zellen im Schnittpunkt der Eingabebänder klassifiziert werden.
Was ist eine Klasse?
Eine Klasse entspricht einer sinnvollen Gruppierung von Positionen. Wald, Wasser und hoher Weizenertrag sind z. B. alle Klassen.
Jede Position wird durch einen Satz oder einen Vektor von Werten, ein Wert für jede Variable, oder ein Eingabeband charakterisiert. Jede Position kann als ein Punkt in einem mehrdimensionalen Attributraum visualisiert werden, dessen Achsen den Variablen in den Eingabebändern entsprechen. Eine Gruppierung der Punkte in diesem mehrdimensionalen Attributraum wird als Cluster bezeichnet. In diesem Fall kann er auch als eine Klasse angesehen werden, da der Cluster auf etwas Sinnvolles verweist. Zwei Positionen gehören zum gleichen Cluster, wenn ihre Attribute (Vektor der Bandwerte) ähnlich sind.
Bekannte Klassen bilden möglicherweise Cluster im Attributraum, wenn die Klassen durch ihre Attributwerte getrennt oder definiert werden können. Positionen, die natürlichen Clustern im Attributraum entsprechen, können so als natürlich auftretende Klassen von Schichten interpretiert werden.
Identifizieren von Klassen für die geordnete Klassifizierung
In einer geordneten Klassifizierung wissen Sie, in welche Klassen Sie das Untersuchungsgebiet aufteilen möchten, und Sie haben Beispielpositionen im Untersuchungsgebiet, die für jede Klasse repräsentativ sind. Wenn Sie z. B. eine Landnutzungskarte aus einem Satellitenbild erstellen, könnten die Klassen Siedlungen, Wasser, Wald, Felder und Straßen sein. Das Ziel besteht darin, jede Position im Untersuchungsgebiet einer bekannten Klasse zuzuweisen. Je mehr Beispielpositionen als zu einer Klasse gehörend identifiziert werden können und je homogener die Zellenwerte innerhalb einer Klasse sind, desto besser fällt die nachfolgende Klassifizierung aus. Die tatsächlichen Positionen, die die bekannten Klassenpositionen bestimmen, werden als Trainingsgebiete bezeichnet.
Die Trainingsgebiete können auf einem Polygon-Layer oder einem Raster bestimmt werden. Wenn Sie die Trainingsgebiete definieren, können Sie ein vorhandenes Raster als Referenz bestimmen. Im Allgemeinen wird eine Farbzusammenstellung der ersten drei Layer im Raster als Hintergrund angezeigt und als Referenz zur Identifizierung von Flächen verwendet, um Bereiche zu identifizieren, die bei der Erzeugung von Trainingsgebieten abgegrenzt werden.
Erstellen von Clustern in einer ungeordneten Klassifizierung
Der erste Schritt bei einer ungeordneten Klassifizierung ist die Erstellung der Cluster. Statistisch sind Cluster natürlich auftretende Gruppierungen in den Daten. Für das Werkzeug Iso Cluster sind Eingabe-Raster-Bänder, die Anzahl der Klassen, der Name der Ausgabesignaturdatei, die Anzahl der Iterationen, die minimale Klassengröße und das Intervall erforderlich, mit dem die Referenzpunkte entnommen werden, mit denen die Cluster berechnet werden (die letzten drei Parameter werden unten erläutert).
Das Werkzeug gibt eine Signaturdatei zurück, die die multivariate Statistik für eine Teilmenge der Zellen für die identifizierten Cluster enthält. Die daraus resultierenden Berechnungen bestimmen, welche Zellenposition zu welchem Cluster gehört, den Mittelwert für den Cluster und die Variance-Covariance-Matrix. Diese Informationen werden in einer ASCII-Signaturdatei gespeichert. Die Signaturdatei ist für die Cluster-Bildung und die Klassifizierung der verbleibenden, nicht erfassten Zellen notwendig.
Speichern von Klassen- oder Cluster-Statistiken: die Signaturdatei
Die Signaturdatei ist eine ASCII-Datei, die die multivariate Statistik für jede Klasse oder jeden Cluster von Interesse speichert. Die Datei enthält den Mittelwert für jede Klasse oder jeden Cluster, die Anzahl der Zellen in der Klasse oder dem Cluster und die Variance-Covariance-Matrix für die Klasse oder den Cluster.
Die Signaturdatei kann mit jedem Texteditor angezeigt werden.
Bei jeder Klasse und jedem Cluster sind die diagonalen Werte, die in der Variance-Covariance-Matrix von oben links nach unten rechts verlaufen, die Varianzwerte für die Variablen, die den Eingabe-Raster-Bändern entsprechen, die durch den Zeilen-/Spaltenschnittpunkt in der Matrix für die Bänder bestimmt wurden. Alle anderen Werte in der Matrix sind Kovarianzwerte.
Wie Cluster für eine ungeordnete Klassifizierung bestimmt werden
Der Name des Algorithmus, der zum Erstellen von Clustern in einer ungeordneten Klassifizierung verwendet wird, ist Iso Cluster. Die Vorsilbe "Iso" des Isodaten-Cluster-Algorithmus steht für Iterative Self Organizing (ISO, iterativ selbstorganisierend), eine Methode zur Durchführung der Cluster-Bildung. Cluster werden mit einer Teilmenge der Zellen im Untersuchungsgebiet berechnet. Alle Cluster-Berechnungen werden mit den Zellenwerten im multivariaten Attributraum durchgeführt und basieren nicht auf räumlichen Eigenschaften. Das heißt, dass der Mittelwert von den Attributwerten für die verschiedenen Eingabe-Bänder abgeleitet wird. Die Varianz- und Kovarianzwerte werden über die Variation innerhalb und zwischen den Bändern berechnet.
Im folgenden Beispiel wird eine K-Mittelwert- bzw. ISO-Cluster-Ansatz verwendet. Die Methodik wird anhand eines Zwei-Bänder-Rasters in der Theorie erklärt. Die gleiche Methodik funktioniert bei einer beliebigen Anzahl eingegebener Bänder oder im n-dimensionalen Raum. Die folgende Erörterung ist konzeptionell, damit der ISO-Cluster-Ansatz leichter verständlich ist.
- Ein leeres Diagramm wird erstellt, mit dem Wertebereich des ersten Bandes entlang der X-Achse und dem Wertebereich des zweiten Bandes entlang der Y-Achse.
- Eine 45-Grad-Linie wird gezogen und in die Anzahl der Klassen unterteilt, die Sie festlegen. Der Mittelpunkt jedes dieser Liniensegmente ist der ursprüngliche Mittelwert für die Klassen.
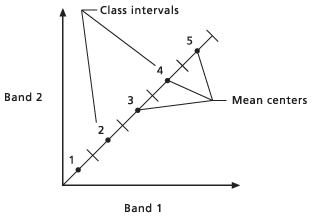
- Jede Referenzzelle wird in das Diagramm geplottet und die Entfernung vom Punkt zu jedem arithmetischen Mittelpunkt auf der 45-Grad-Linie wird bestimmt. Die Entfernung wird im Attributraum mit dem Satz des Pythagoras berechnet. Der Referenzpunkt wird dem Cluster zugewiesen, der durch den nächstgelegenen arithmetischen Mittelpunkt dargestellt wird.
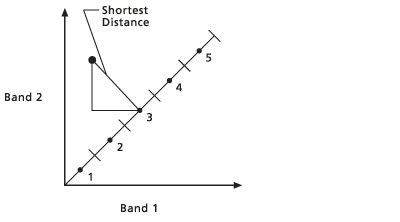
- Der nächste Referenzpunkt wird geplottet und das oben erläuterte Verfahren wird für alle Referenzpunkte wiederholt.
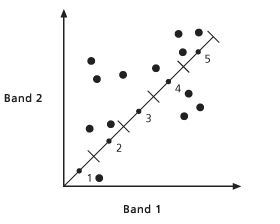
- Der oben erläuterte Vorgang wird wiederholt. Vor der nächsten Wiederholung wird ein neuer arithmetischer Mittelpunkt für jeden Cluster auf Grundlage der Werte der Zellenpositionen berechnet, die dem Cluster in der vorherigen Iteration zugewiesen wurden. Mit dem neuen arithmetischen Mittelpunkt für jeden Cluster werden die vorherigen zwei Schritte wiederholt.
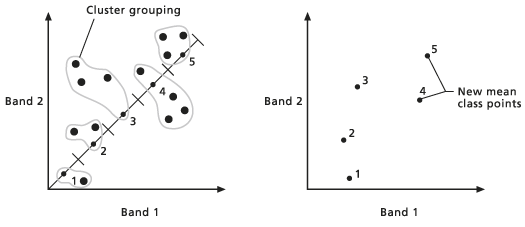
- Die Mittelwerte werden aktualisiert, und der vorherige Schritt wird wiederholt. Der Iterationsprozess der Aktualisierung der Mittelwerte wird fortgesetzt, bis die benutzerdefinierte Anzahl von Iterationen erreicht wird oder bis sich weniger als 2 Prozent der Zellen relativ zum neuen Mittelwert bei einer Iteration von einem Cluster zum anderen ändern.
Die Cluster-Bildung reagiert auf die Wertebereiche in den einzelnen Bändern. Dieser Wertebereich bestimmt die Werte auf der X- und Y-Achse, mit denen die euklidischen Entfernungen zwischen Mittelwert- und Referenzpunkten berechnet werden. Damit die Attribute der einzelnen Bänder gleich verarbeitet werden, sollte für jedes Band ein ähnlicher Wertebereich verwendet werden, unabhängig davon, ob eine geordnete Klassifizierung oder eine ungeordnete Cluster-Bildung durchgeführt wird. Wenn der Wertebereich von einem Band verglichen mit den anderen Bändern relativ klein ist, ist die euklidische Entfernung im multivariaten Raum möglicherweise so klein, dass mehrere Cluster möglicherweise den Mittelwert Null aufweisen. Wenn irgendein Cluster den Mittelwert Null hat, schlagen die abschließende Klassifizierung und alle anderen multivariaten Werkzeuge, die von einer Signaturdatei abhängen, fehl. Im Idealfall sollten alle Bänder auf den gleichen Wertebereich normalisiert werden.