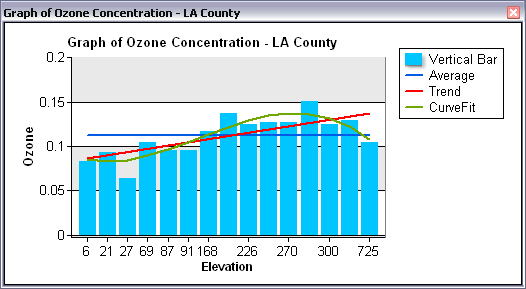
Die visuellen und analytischen Vorteile von Diagrammen können durch Hinzufügen einer Funktion noch erweitert werden. Durch die Funktion wird eine bestimmte mathematische oder statistische Operation auf die Werte in der Datenreihe angewendet. Das Ergebnis wird als Linie im Diagramm angezeigt.
Funktionskategorien
Unter den Diagrammwerkzeugen der Anwendung ArcGIS Desktop sind 16 Funktionstypen verfügbar. Diese können in zwei allgemeine Kategorien eingeteilt werden: "Beschreibend" und "Trend".
Beschreibend
Mit einer beschreibenden Funktion wird aus allen Werten in einer Reihe ein einzelner Wert berechnet. Dieser Funktionstyp wird als gerade Linie im Diagramm angezeigt, die den berechneten Wert darstellt.
Beschreibende Funktionstypen
| Funktionstyp | Beschreibung |
|---|---|
Mittelwert | Ein aus den Werten gebildeter Mittelwert. |
Anzahl | Die Anzahl der Werte in der Reihe (n). |
Hoch | Der höchste Wert in der Reihe. |
Niedrig | Der kleinste Wert in der Reihe. |
Medianwert | Der Medianwert der Reihe. |
Modus | Der Moduswert der Reihe. |
RMS | Der RMS-(Root Mean Square-)Wert der Reihe. Die allgemeine Formel für RMS lautet: |
Standardabweichung | Ein Maß für die Verteilung der Werte in der Reihe. Die allgemeine Formel lautet: |
Varianz | Die Varianz entspricht der Verteilung der Werte in der Reihe. Sie wird als Mittelwert der Quadratabweichungen jeder Zahl von ihrem Mittelwert berechnet. |
(n entspricht dabei der Anzahl der Werte.)
Trend
Trendfunktionen illustrieren die Richtung der Änderung von Werten. Trendfunktionen können lokal oder global sein. Sie zeigen eine globale Zusammenfassung des Wertebereichs in einem Diagramm an.
| Funktionstypen | Beschreibung |
|---|---|
Trend | Eine lineare Beziehung, die als gerade Linie mit einer bestimmten Neigung dargestellt wird. |
Exponentieller Trend | Eine geschwungene Linie, die eine exponentielle Beziehung darstellt. |
Durch andere Trends wird eine lokale Zusammenfassung berechnet, durch die die Werte generalisiert oder geglättet werden.
| Typen mit lokaler Zusammenfassung | Beschreibung |
|---|---|
Gleitender Durchschnitt | Für jeden Wert in der Reihe wird der Durchschnitt (einfach oder gewichtet) für eine Teilmenge benachbarter Werte berechnet. Dies ist hilfreich, um Langzeittrends besser von zyklischen Trends zu unterscheiden. |
Exponentieller gleitender Durchschnitt | Vergleichbar mit dem gleitenden Durchschnitt, mit der Ausnahme, dass dieser Trend gewichtet ist. Die Werte in der Teilmenge, die näher am berechneten Wert liegen, erhalten also eine stärkere Gewichtung. |
Kurvenanpassung | Eine geglättete Kurve wird auf der Grundlage der Werte in der Reihe generiert, indem eine Gauß'sche Polynomialfunktion angewendet wird. "Polynomischer Grad" wird verwendet, um die Reihenfolge (Anzahl der Koeffizienten) des verwendeten Polynoms zu steuern. |
Glätten | Eine geglättete Kurve wird auf der Grundlage der Werte in der Reihe generiert, indem eine Spline-Funktion auf die Werte angewendet wird. Je höher der Faktor, desto glatter die Kurve (basiert auf Martijn van Engelands B-Spline-Komponente). |
Ein weiterer Trend ist der kumulative Trend. Dabei wird die kumulative Menge der Werte dargestellt:
Kumulativ | Jeder Wert wird zum vorherigen Wert addiert, um den Grad der Steigerung darzustellen. |
Parameter
Die Mehrheit der Funktionstypen wird direkt auf der Grundlage der Datenreihe erstellt. Einige Funktionen erfordern, dass zusätzliche Parameter festgelegt werden. Dazu gehören: Kurvenanpassung, Gleitender Durchschnitt, RMS, Glätten und Standardabweichung.