Funktionsweise des Werkzeugs "Natürlicher Nachbar"

Mit der Spatial Analyst-Lizenz verfügbar.

Der Algorithmus, der von dem Interpolationswerkzeug Natürlicher Nachbar verwendet wird, sucht nach der nächstgelegenen Teilmenge von Eingabemessungen zu einem Abfragepunkt und weist diesen Daten proportional zur Fläche eine Gewichtung zu, um den gesuchten Punkt zu interpolieren (Sibson, 1981). Sie wird auch als Sibson- oder "Area-Stealing"-Interpolation bezeichnet. Zu den grundlegenden Eigenschaften dieser Interpolation gehört die lokale Begrenzung, da lediglich eine Teilmenge von Eingabemessungen um den gesuchten Punkt berücksichtigt wird, und die Tatsache, dass interpolierte Höhen immer innerhalb des Bereichs liegen, der durch die Eingabemessungen begrenzt wird. Sie berücksichtigt keine Trends und produziert keine Spitzen, Löcher, Kämme oder Täler, wenn diese nicht in den Eingabemessungen vorhanden sind. Die resultierende Oberfläche berührt die verwendeten Eingabemessungen und ist eben, abgesehen von den Bereichen um die Eingabemessungen.

Tipp:

Wenn Sie über die 3D Analyst-Erweiterung verfügen, können Sie das Werkzeug TIN zu Raster verwenden, um Bruchkanten in die Interpolation zu integrieren. Dadurch lassen sich unter Umständen die Ergebnisse der Interpolation verbessern, indem in den entsprechenden Bereichen, z. B. an Straßenrändern oder Gewässern, lineare Unterbrechungen entstehen. Die Interpolation folgt der lokalen Struktur der Eingabedaten und erfordert keine Eingaben des Benutzers zur Radiusbestimmung, Anzahl der Messpunkte oder Formbestimmung. Sie liefert gleich gute Ergebnisse sowohl bei gleichmäßig als auch bei ungleichmäßig verteilten Daten (Watson 1992).

Die "natürlichen Nachbarn" eines Punktes werden durch die Punkte der benachbarten Voronoi- (d. h. Thiessen-) Polygone definiert. Zunächst wird ein Voronoi-Diagramm aller angegebenen Punkte konstruiert, das durch die oliv gefärbten Polygone wiedergegeben wird. Anschließend wird ein neues Voronoi-Polygon, in beige, um den zu interpolierenden Punkt (rotes Sternchen) erstellt. Die Proportionen der Überlappungen zwischen diesem neuen Polygon und den anfänglichen Polygonen werden dann zur Bestimmung der Gewichtungen verwendet.

Beispiel für ein Voronoi-Polygon, das um einen Interpolationspunkt erstellt wurde

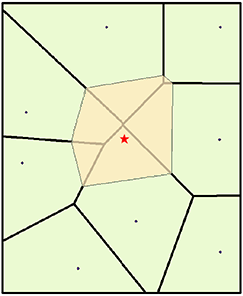
Im Vergleich dazu würde ein entfernungsbasiertes Interpolationswerkzeug wie IDW (Inverse Distance Weighted) dem nördlichsten Punkt und dem nordöstlichen Punkt ähnliche Gewichtungen zuweisen, da sie eine ähnliche Entfernung vom Interpolationspunkt aufweisen. Bei der Interpolationsmethode "Natürlicher Nachbar" werden jedoch die Gewichtungen 19,12 Prozent und 0,38 Prozent zugewiesen, und zwar basierend auf der prozentualen Überlappung.

Referenzen

Sibson, R. "A Brief Description of Natural Neighbor Interpolation," chapter 2 in Interpolating Multivariate Data. New York: John Wiley & Sons, 1981. 21–36.

Watson, D., Contouring: A Guide to the Analysis and Display of Spatial Data. London: Pergamon Press, 1992.