Mit der Spatial Analyst-Lizenz verfügbar.
Mit der 3D Analyst-Lizenz verfügbar.
Das Werkzeug Schummerung berechnet die hypothetische Beleuchtung einer Oberfläche durch die Bestimmung von Beleuchtungswerten für jede Zelle in einem Raster. Dies geschieht durch Festlegen der Position einer hypothetischen Lichtquelle und Berechnen der Beleuchtungswerte für jede Zelle in Bezug zu den benachbarten Zellen. Mithilfe dieser Funktion kann die Visualisierung einer Oberfläche für die Analyse oder die grafische Anzeige stark verbessert werden, insbesondere bei Verwendung von Transparenz.
Licht und Schatten sind standardmäßig Graustufen, die mit ganzen Zahlen von 0 bis 255 verknüpft sind (zunehmend von schwarz zu weiß).
Parameter "Schummerung"
Der primäre Faktor beim Erstellen einer Schummerungs-Karte für einen bestimmten Standort ist die Position der Sonne am Himmel.
Azimut
Der Azimut ist die Winkelrichtung der Sonne, gemessen von Norden im Uhrzeigersinn von 0 bis 360 Grad. Ein Azimut von 90 Grad steht für Osten. Der Standardazimut ist 315 Grad (NW).

Höhe
Die Höhe ist der Winkel der Beleuchtungsquelle über dem Horizont. Die Einheiten werden in Grad von 0 (am Horizont) bis 90 Grad (direkt über dem Objekt) gemessen. Die Standardeinstellung ist 45 Grad.
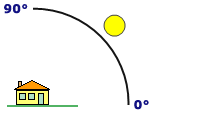
Im nachfolgenden Beispiel hat die Schummerung einen Azimut von 315 Grad und eine Höhe von 45 Grad.

Verwenden von Schummerung für die Anzeige
Durch die Platzierung eines Höhenrasters auf einem Schummerungs-Raster und die Anpassung der Transparenz des Höhenrasters können Sie einfach eine optisch ansprechende Reliefkarte einer Landschaft erstellen.

Sie können weitere Layer wie Landnutzungsarten, Vegetation, Straßen oder Wasserläufe hinzufügen, um den Informationsgehalt der Anzeige zu erhöhen.
Verwenden von Schummerung bei der Analyse
Durch Modellieren des Schattens (Standardeinstellung) können Sie die lokale Beleuchtung berechnen und prüfen, ob die Zelle im Schatten liegt oder nicht.
Ferner lässt sich durch die Modellierung des Schattens jede Zelle ermitteln, die zu einer bestimmten Tageszeit im Schatten einer anderen Zelle liegt. Zellen im Schatten einer anderen Zelle werden mit 0 kodiert. Alle anderen Zellen werden mit ganzen Zahlen von 1 bis 255 kodiert. Sie können alle Werte größer 1 als 1 reklassifizieren, wodurch sich ein binäres Ausgabe-Raster ergibt. Im folgenden Beispiel befinden sich die schwarzen Bereiche im Schatten. Der Azimut ist in allen Abbildungen identisch, der Sonnenwinkel (die Höhe) wurde jedoch geändert.

Berechnung der Schummerung
Um den Schummerungswert zu berechnen, werden zunächst Höhe und Azimut der Beleuchtungsquelle benötigt. Diese Werte werden mit den Berechnungen für Neigung und Ausrichtung verarbeitet, um den endgültigen Schummerungswert für jede Zelle im Ausgabe-Raster zu bestimmen.
Schummerungsalgorithmus
Der Algorithmus zur Berechnung des Schummerungswertes lautet wie folgt:
(1) Schummerung = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) +
(sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))Beachten Sie: Wenn aus der Berechnung des Schummerungswertes ein Ergebnis < 0 hervorgeht, ergibt sich daraus, dass der Ausgabezellwert = 0 ist.
Berechnen des Beleuchtungswinkels
Die Höhe der Beleuchtungsquelle wird in Graden über der Horizontalen angegeben. Für die Berechnungsformel des Schummerungswertes ist jedoch eine Darstellung des Winkels in Radianten erforderlich. Außerdem muss er der Ablenkung von der Vertikalen entsprechen. Die Richtung von der Oberfläche direkt nach oben (direkt darüber) wird als "Zenit" bezeichnet. Der Zenitwinkel wird vom Zenitpunkt in Richtung der Beleuchtungsquelle gemessen und entspricht dem 90-Grad-Komplement der Höhe. Um den Beleuchtungswinkel zu berechnen, besteht der erste Schritt in der Umrechnung des Höhenwinkels in den Zenitwinkel. Der zweite Schritt besteht im Umrechnen des Winkels in Radianten.
Höhenwinkel in Zenitwinkel konvertieren:
(2) Zenith_deg = 90 - HöheIn Radianten konvertieren:
(3) Zenith_rad = Zenit * pi / 180.0Berechnen der Beleuchtungsrichtung
Die Richtung der Beleuchtungsquelle, Azimut, wird in Graden angegeben. Für die Schummerungsformel muss dieser Winkel in Radianteneinheiten vorliegen. Zunächst wird der Azimutwinkel von der geographischen Einheit (Kompassrichtung) in eine mathematische Einheit (rechter Winkel) umgerechnet. Im nächsten Schritt wird der Azimutwinkel in Radianten konvertiert.
Azimutwinkel anpassen:
(4) Azimuth_math = 360.0 - Azimut + 90Beachten Sie: Wenn Azimuth_math >= 360,0, dann:
(5) Azimuth_math = Azimuth_math - 360.0In Radianten konvertieren:
(6) Azimuth_rad = Azimuth_math * pi / 180.0Berechnen der Neigung und Ausrichtung
Ein sich bewegendes 3x3-Fenster durchläuft jede Zelle im Eingabe-Raster. Für jede Zelle in der Mitte des Fensters werden ein Ausrichtungs- und ein Neigungswert anhand eines Algorithmus berechnet, der die Werte der acht angrenzenden Zellen mit berücksichtigt. Die Zellen werden als Buchstaben a bis i identifiziert, wobei e die Zelle darstellt, für die die Ausrichtung berechnet wird.
Die Änderungsrate in der x-Richtung für Zelle e wird mit dem folgenden Algorithmus berechnet:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize)Die Änderungsrate in der y-Richtung für Zelle e wird mit dem folgenden Algorithmus berechnet:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)Das steilste Gefälle für eine Zelle in der Oberfläche ist die Neigung. Der Algorithmus zur Berechnung der Neigung in Radianten, einschließlich Z-Faktor, lautet:
(9) Slope_rad = ATAN (z_factor * √ ([dz/dx]2 + [dz/dy]2)) Die Richtung der steilsten Neigungsrichtung ist die Ausrichtung. Die Ausrichtung in Radianten wird im Bereich von 0 bis 2 Pi definiert, wobei 0 Osten ist. Die Ausrichtung wird anhand der Regeln mit folgendem Algorithmus ermittelt:
(10) If [dz/dx] is non-zero:
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2 * pi + Aspect_rad If [dz/dx] is zero:
if [dz/dy] > 0 then Aspect_rad = pi / 2 else if [dz/dy] < 0 then Aspect_rad = 2 * pi - pi / 2 else Aspect_rad = Aspect_radBeispiel für die Berechnung der Schummerung
Ein Beispiel: Der Schummerungswert der mittleren Zelle des beweglichen Fensters wird berechnet.
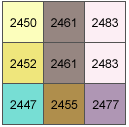
Die Zellengröße beträgt 5 Einheiten. Für die Höhe wird der Standardwert 45 Grad und für den Azimut 315 Grad verwendet.
- Beleuchtungswinkel
Die Berechnung des Zenitwinkels aus Gleichung 2 lautet:
(2) Zenith_deg = 90 - Höhe = 90 - 45 = 45Und konvertiert in Radianten aus Gleichung 3:
(3) Zenith_rad = Zenith_deg * pi / 180.0 = 45 * 3.1428571429 / 180 = 0.7857142857 - Die Beleuchtungsrichtung
Die Berechnung für die Umwandlung des Azimutwinkels von einem geographischen in einen mathematischen Winkel mit Gleichung 4 lautet:
(4) Azimuth_math = 360.0 - Azimut + 90 = 360.0 - 315 + 90 = 135 = 2.3571428571Die Umwandlung von Azimutwinkel in Radianten mit Gleichung 6 lautet:
(6) Azimuth_rad = Azimuth_math * pi / 180.0 = 135 * 3.1438571429 / 180
- Neigung und Ausrichtung
Die Berechnung für die Änderungsrate in der x-Richtung für die mittlere Zelle e lautet:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize) = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801)/ 40 = 3.125Die Berechnung für die Änderungsrate in der y-Richtung für die mittlere Zelle e lautet:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525Die Berechnung des Neigungswinkels lautet:
(9) Slope_rad = ATAN ( z_factor * √ ([dz/dx]2 + [dz/dy]2)) = atan(1 * sqrt(3.125 * 3.125 + -0.525 * -0.525)) = 1.26511Die Berechnung für den Winkel Aspect_rad von Regel 10 lautet (da dz/dx in diesem Beispiel ungleich Null ist):
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600412Da der Wert niedriger als 0 ist, wird dieser Teil der Regel angewendet:
Aspect_rad = 2 * pi + Aspect_rad = 2 * 3.1428571429 + -2.9751469600412 = 3.310567 - Schummerung
Die endgültige Berechnung der Schummerung lautet:
HSchummerung = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) = 255.0 * ((cos(0.7857142857) * cos(1.26511)) + (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567))) = 153.82
Wenn das Ausgabe-Raster vom Typ "Integer" ist, lautet der Schattenwert für die mittlere Zelle e = 154.
Referenzen
Burrough, P. A. and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), S. 190