Beschreibung
Mit dem Werkzeug Transformieren werden Daten aus einem Koordinatensystem in ein anderes konvertiert. Oftmals wird es verwendet, um in Digitalisiereinheiten (meistens Zoll) erstellte Coverages in reale, auf dem Kartenmanuskript darstellbare Einheiten zu konvertieren. Diese realen Orte werden anhand einer bestimmten Projektion dargestellt. So kann es sich bei der Projektion Ihrer Grundkarte beispielsweise um UTM mit in Metern gemessenen Passpunktpositionen handeln.
Um eine Transformation durchzuführen, müssen Sie in Ihrem Coverage mindestens zwei Tics für reale Orte registrieren können. Diese realen Orte können mithilfe des Grundkartenkoordinatensystems in Fuß oder in Meter gemessen werden. Sie können sich auch an Schnittstellen von Längen-/Breitengraden befinden. Wenn Ihre Orte mit Längen- und Breitengraden angegeben sind, können Sie mit dem Werkzeug Projizieren die Passpunkte in das Koordinatensystem konvertieren, das Ihrer in Fuß oder Meter gemessenen Grundkarte entspricht. Führen Sie dies vor dem Transformieren des digitalisierten Coverages aus.
Wenn Sie die Daten zum ersten Mal transformieren, führen Sie eine Transformation in dieselbe Projektion wie die Quellkarte aus. Sie können anschließend mit dem Werkzeug "Projizieren" das Coverage in eine andere Kartenprojektion konvertieren.
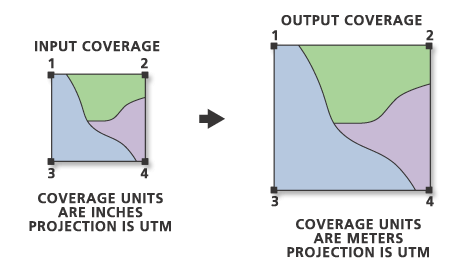
Das Werkzeug "Transformieren" basiert auf einem Vergleich der Koordinaten von Tics im Eingabe-Coverage mit den Koordinaten entsprechender Tics im Ausgabe-Coverage. Die zu vergleichenden Tics werden durch die Tic-IDs angegeben. Die Mindestanzahl benötigter Tics hängt von der jeweils verwendeten Transformationsoption ab. Tics werden bei der Transformation als Passpunkte behandelt und nicht mit der Transformationsgleichung konvertiert. Die Koordinaten der Ausgabe-Tics sind nach der Transformation unverändert. Features, die mit den Eingabe-Tics übereinstimmen, stimmen jedoch in der Regel nicht mit den Ausgabe-Tics überein. Möglicherweise müssen Sie Features anpassen, damit sie nach der Transformation mit den Tics im Ausgabe-Coverage übereinstimmen.
Mit dem Werkzeug "Transformieren" wird standardmäßig eine Funktion für die affine Transformation verwendet, um Coverage-Koordinaten aus dem Eingabe-Coverage in das Ausgabe-Coverage zu transformieren. Zur Berechnung einer affinen Transformation sind mindestens drei Tics erforderlich.
Bei einer affinen Transformation können die Daten unterschiedlich skaliert, verzerrt, gedreht und übertragen werden. In der folgenden Grafik sind die vier möglichen Änderungen dargestellt.
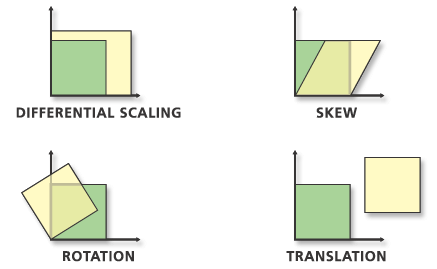
Die Funktion für die affine Transformation lautet wie folgt:
x’ = Ax + By + CDie Parameter A-F werden durch die Passpunkte festgelegt,
y’ = Dx + Ey + Fund dann auf alle Koordinaten im Coverage angewendet.
Dabei sind x und y Koordinaten des Eingabe-Coverages und x’ und y’ Koordinaten des Ausgabe-Coverages. A, B, C, D, E und F werden durch einen Vergleich der Positionen von Tics im Eingabe-Coverage und ihren Positionen im Ausgabe-Coverage bestimmt. Mit ihnen werden die Tic-Koordinaten skaliert, verzerrt, gedreht und übertragen.
Das Werkzeug "Transformieren" gibt die sechs Parameter und ihre geometrische Interpretation an. Es folgt ein Beispiel für einen Teil des ausgegebenen Berichts zu einer affinen Transformation.
Transformieren von Koordinaten für Coverage "in_cov_name"
Scale (X,Y) = (246.140,255.702) Skew (degrees) = (-0.061)
Rotation (degrees) = (0.334) Translation = (2890.267,3679.906)
RMS Error (input, output) = (0.084,20.592)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = 246.135 B = -1.763 C = 2890.267
D = 1.434 E = 255.696 F = 3679.906
In einem Abschnitt des Berichts sind die Parameter der Transformationsgleichungen aufgelistet. Sie können die Gleichungsparameter interpretieren, um zu verstehen, was in geometrischer Hinsicht geschieht. Der erste Abschnitt des Berichts gibt die interpretierten Werte für Skalierung, Verzerrung und Rotation an. Durch eine Änderung der Reihenfolge, in der diese geometrischen Aktionen angewendet werden, werden deren interpretierte Werte geändert, doch sind das Endergebnis und die Gleichungsparameter immer gleich. Die Interpretation wird in der Reihenfolge (1) Skalierung, (2) Verzerrung in X-Richtung und (3) Rotation von Punkten um die Achsen entgegen dem Uhrzeigersinn durchgeführt. Die Übertragungswerte werden nicht interpretiert, sondern sind einfach die Übertragungsparameter C und F aus den Gleichungen. Mit dem Werkzeug "Transformieren" werden die Parameter der affinen Gleichung wie folgt interpretiert:
A = mx · cos t
B = my · (k · cos t - sin t)
D = mx · sin t
E = my · (k · sin t + cos t)
C = translation in x direction
F = translation in y direction
where
mx = change of scale in x direction
my = change of scale in y direction
k = shear factor along the x-axis = tan (skew angle) (the skew angle is measured from the y-axis)
t = rotation angle, measured counterclockwise from the x-axis
Der Rotationswinkel bezieht sich auf die Rotation der Daten in einem festen XY-Koordinatensystem. In der vorherigen Abbildung wurden die ursprünglichen Daten um 45 Grad gedreht. Ein negativer Wert bedeutet, dass die Daten in Bezug auf die X-Achse im Uhrzeigersinn gedreht werden.
Mit der Ähnlichkeitstransformation werden die Daten skaliert, gedreht und übertragen. Die Achsen werden nicht unabhängig skaliert. Außerdem wird keine Verzerrung vorgenommen. Für die Ähnlichkeitstransformation werden mindestens zwei Passpunkte benötigt. Im folgenden Bericht wird eine Ähnlichkeitstransformation beschrieben. Es wurden dieselben Coverages verwendet, die zuvor mit einer affinen Transformation transformiert wurden.
Transformieren von Koordinaten für Coverage "in_cov_name"
Scale (X,Y) = (249.927,249.927)
Rotation (degrees) = (0.362) Translation = (2855.407,3715.168)
RMS Error (input, output) = (0.118,29.398)
Similarity X = Ax + By + C
Y = -Bx + Ay + F
A = 249.922 B = -1.578
C = 2855.407 F = 3715.168
Beachten Sie, dass die X- und Y-Maßstabswerte gleich sind. Ein Verzerrungswert ist nicht angegeben, da bei einer Ähnlichkeitstransformation eine nicht orthogonale Verschiebung der Daten unzulässig ist.
Die Funktion der Ähnlichkeitstransformation lautet
x’ = Ax + By + C
y’ = -Bx + Ay + F
where
A = s · cos t
B = s · sin t
C = translation in x direction
F = translation in y direction
and
s = scale change (same in x and y directions)
t = rotation angle, measured counterclockwise from the x-axis
Wie bei der Erläuterung zur affinen Transformation bezieht sich der Rotationswinkel auf die Rotation der Daten in einem festen XY-Koordinatensystem. In der vorherigen Abbildung wurden die ursprünglichen Daten um 45 Grad gedreht. Ein negativer Wert bedeutet, dass die Daten, von der X-Achse aus gemessen, im Uhrzeigersinn gedreht werden.
Die projektive Transformation basiert auf einer komplexeren Formel, für die mindestens vier Tics erforderlich sind.
x’ = (Ax + By + C) / (Gx + Hy + 1)
y’ = (Dx + Ey + F) / (Gx + Hy + 1)Der Bericht zu einer projektiven Transformation beinhaltet den ungefähren Maßstab, den RMS-Fehler und die Gleichungsparameter. Aufgrund der Komplexität der Interpretation werden die Parameter der projektiven Transformation nicht interpretiert. Weitere Informationen finden Sie unter den photogrammetrischen Texten, die in den Referenzen am Ende dieses Themas aufgeführt sind. Es folgt ein Beispiel eines ausgegebenen Berichts zu einer projektiven Transformation.
Transformieren von Koordinaten für Coverage "in_cov_name"
Approximate scale = 1479.087
RMS Error (input, output) = (0.040,60.878)
2D Projective X = (Ax + By + C) / (Gx + Hy + 1)
Y = (Dx + Ey + F) / (Gx + Hy + 1)
A = 55.667 B = -718.999 C = 2125052.558
D = -199.525 E = 1385.541 F = 317759.475
G = -0.001 H = 0.000
Principal point of input (xp,yp) = (2.000,16.946)
Exposure center of output(Xc,Yc) = (2127791.000,343183.000)
Der Hauptpunkt und der Lagemittelpunkt entsprechen dem ersten Tic in der Tic-Datei des Eingabe-Coverages. Wenn Sie einen anderen Punkt verwenden möchten (z. B. den Mittelpunkt des Datasets), stellen Sie sicher, dass es sich um den ersten Tic in der Datei handelt.
Ein RMS-Fehler (Root Mean Square) wird für jede ausgeführte Transformation berechnet. Er gibt an, wie gut die abgeleitete Transformation ist. Im folgenden Beispiel ist die relative Position von vier Ausgabe-Passpunkten (Tics) und den transformierten Eingabe-Passpunkten dargestellt:
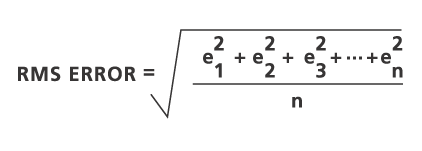
Der RMS-Fehler misst die Fehler zwischen den Tics des Ausgabe-Coverages und den transformierten Positionen der Tics des Eingabe-Coverages.
Die Transformation wird anhand der Methode der kleinsten Quadrate abgeleitet, sodass mehr Tics als nötig erstellt werden können.
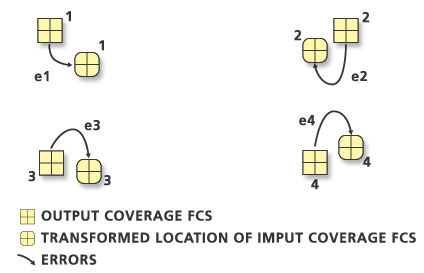
Der RMS-Fehler für die einzelnen Transformationen wird sowohl in den Eingabe-Coverage-Einheiten (z. B. 0,031 Zoll) als auch in den Ausgabe-Coverage-Einheiten (z. B. 37,465 Fuß) angegeben.
RMS Error (input, output) = (0.031,37.465)Eine perfekte Transformation ergibt einen RMS-Fehler von null. Sie werden zwar keinen Wert 0,000 erreichen, sollten den RMS jedoch so gering wie möglich halten. Es ist empfehlenswert, einen maximal zulässigen Fehler festzulegen und beizubehalten. Zulässige Werte sind je nach Genauigkeit der Ursprungsdaten und dem Maßstab der Quellkarte verschieden. Hohe RMS-Fehler zeigen an, dass die alten und die neuen Tics nicht denselben relativen Positionen entsprechen. Wenn der RMS-Fehler höher als der festgelegte Wert ist, kann dies auf Konvertierungsprobleme hinweisen, die zu einer falschen Streckung des Ausgabe-Coverages führen können.
Im letzten Teil des Berichts sind die Eingabe- und Ausgabe-Tic-Koordinaten sowie ihre X- und Y-Fehler aufgelistet (siehe unten). Die Transformationsparameter sind der bestmögliche Kompromiss zwischen den Eingabe- und Ausgabe-Tics. Wenn Sie mit den Transformationsparametern die tatsächlichen Eingabe-Tics transformieren, stimmen die transformierten Ausgabepositionen nicht mit den tatsächlichen Positionen der Ausgabe-Tics überein. Die X- und Y-Fehler sind eine Maßeinheit für die Übereinstimmung der tatsächlichen Positionen mit den transformierten Positionen der Ausgabe-Tics. Sie können manchmal einen Fehler entdecken, indem Sie sich die X- und Y-Fehler ansehen.
tic id input x input y output x output y x error y error ------------------------------------------------------------------------ 1 2.000 16.946 2127791.000 343183.000 14.463 75.499 2 12.764 16.821 2143469.000 343326.000 -31.043 -85.363 3 2.052 1.976 2128000.000 320680.000 -36.290 -2.353 4 12.922 2.013 2143729.000 320912.000 20.245 -6.163 5 2.082 9.442 2127944.000 332015.000 22.016 -74.699 6 12.662 9.442 2143320.000 332015.000 10.609 93.079
Beispiel
In diesem Beispiel wird ein Coverage aus Einheiten des Digitalisierungsgeräts in reale Koordinaten transformiert. Das ursprüngliche Coverage mit dem Namen INCHCOV weist die folgenden Passpunkte auf, die in Zoll des Digitalisierungsgeräts gemessen wurden:
IDTIC XTIC YTIC 1 2.000 16.946 2 12.764 16.821 3 2.052 1.976 4 12.922 2.013 5 2.082 9.442 6 12.662 9.442
Für die Grundkarte wurde das State-Plane-Koordinatensystem verwendet. Passpunkte wurden in Fuß gemessen. Jedes Tic entspricht den folgenden Positionen:
Tic-IDs X Coordinates Y Coordinates 1 2,127,791 343,183 2 2,143,469 343,326 3 2,128,000 320,680 4 2,143,729 320,912 5 2,127,944 332,015 6 2,143,320 332,015
Das Ausgabe-Coverage muss vorhanden sein, bevor das Werkzeug "Transformieren" ausgeführt werden kann. Mit dem Werkzeug Coverage erstellen können Sie das Ausgabe-Coverage erstellen und die TIC- und BND-Dateien gegebenenfalls aus dem Eingabe-Coverage kopieren. Optional können Sie mit dem Werkzeug Generate ein neues Coverage erstellen, das Tics an den gewünschten Positionen enthält.
Die TIC-Datei für das Ausgabe-Coverage muss XY-Koordinaten für jedes Tic enthalten, das im Ausgabe-Coverage beibehalten werden soll. Dies sind in diesem Fall die TIC-Positionen im State-Plane-Koordinatensystem. Tic-Koordinaten können in ArcMap oder in den Modulen TABLES oder INFO von ArcInfo Workstation angepasst werden.
Sobald die neuen Tics erstellt wurden, können die Features im digitalisierten Coverage in reale Einheiten transformiert werden. Das Werkzeug "Transformieren" wird verwendet, um ein State-Plane-Projektions-Coverage in Zoll (INCHCOV) in ein State-Plane-Projektions-Coverage in Fuß (STATECOV) zu konvertieren. Es folgt ein Beispiel für die affine Transformation.
Scale (X,Y) = (1452.317,1508.433) Skew (degrees) = (0.416)
Rotation (degrees) = (0.218) Translation = (2124994.654,317664.385)
RMS Error (input, output) = (0.048,71.614)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = 1452.230 B = -5.526 C = 2124994.654
D = 15.858 E = 1508.462 F = 317664.385
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 14.463 75.499
2 12.764 16.821
2143469.000 343326.000 -31.043 -85.363
3 2.052 1.976
2128000.000 320680.000 -36.290 -2.353
4 12.922 2.013
2143729.000 320912.000 20.245 -6.163
5 2.082 9.442
2127944.000 332015.000 22.016 -74.699
6 12.662 9.442
2143320.000 332015.000 10.609 93.079
Es folgt das entsprechende Beispiel einer projektiven Transformation für dasselbe Coverage. Denken Sie daran, dass die Option PROJECTIVE normalerweise nur verwendet wird, wenn die ursprünglichen Coverages direkt aus Luftaufnahmen digitalisiert wurden.
Transformieren von Koordinaten für Coverage "INCHCOV"
Approximate scale = 1479.087
RMS Error (input, output) = (0.040,60.878)
2D Projective X = (Ax + By + C) / (Gx + Hy + 1)
Y = (Dx + Ey + F) / (Gx + Hy + 1)
A = 55.667 B = -718.999 C = 2125052.558
D = -199.525 E = 1385.541 F = 317759.475
G = -0.001 H = 0.000
Principal point of input (xp,yp) = (2.000,16.946)
Exposure center of output(Xc,Yc) = (2127791.000,343183.000)
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 -4.438 45.252
2 12.764 16.821
2143469.000 343326.000 -11.447 -36.202
3 2.052 1.976
2128000.000 320680.000 -17.300 46.421
4 12.922 2.013
2143729.000 320912.000 1.704 -36.962
5 2.082 9.442
2127944.000 332015.000 21.787 -93.410
6 12.662 9.442
2143320.000 332015.000 9.694 74.901
Zum Schluss folgt dasselbe Coverage, das mit der Option SIMILARITY transformiert wurde.
Transformieren von Koordinaten für Coverage "inchcov"
Scale (X,Y) = (1483.794,1483.794)
Rotation (degrees) = (0.377) Translation = (2124800.900,317942.729)
RMS Error (input,output) = (0.162,240.958)
Similarity X = Ax + By + C
Y = -Bx + Ay + F
A = 1483.762 B = -9.765
C = 2124800.900 F = 317942.729
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 -188.053 -76.916
2 12.764 16.821
2143469.000 343326.000 106.378 -300.277
3 2.052 1.976
2128000.000 320680.000 -173.717 214.680
4 12.922 2.013
2143729.000 320912.000 225.411 143.724
5 2.082 9.442
2127944.000 332015.000 -146.109 -42.262
6 12.662 9.442
2143320.000 332015.000 176.089 61.051
Im folgenden Beispiel wird ein Coverage mit einer affinen Transformation umgekehrt.
Transformieren von Koordinaten für Coverage "flag"
Scale (X,Y) = (1.000,-1.000) Skew (degrees) = (0.000)
*** Negative Y scaling indicates reflection around X axis. ***
Rotation (degrees) = (180.000) Translation = (800.000,0.000)
RMS Error (input, output) = (0.000,0.000)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = -1.000 B = 0.000 C = 800.000
D = 0.000 E = 1.000 F = 0.000
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 700.000 100.000
100.000 100.000 0.000 0.000
2 700.000 800.000
100.000 800.000 0.000 0.000
3 100.000 800.000
700.000 800.000 0.000 0.000
4 100.000 100.000
700.000 100.000 0.000 0.000
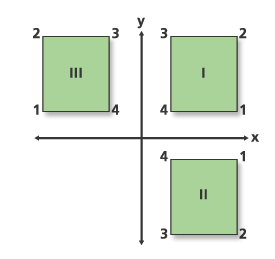
Beachten Sie die Meldung zur Reflexion im ausgegebenen Bericht. In der folgenden Grafik ist dargestellt, was mit dem Coverage geschieht. Das Rechteck mit der Beschriftung I ist das Eingabe-Coverage. Es wird ein Y-Maßstab von -1 auf die Koordinaten angewandt. Dies führt zum Rechteck II. Es ist kein Verzerrungsfaktor vorhanden, sodass die Punkte um 180° gedreht und dadurch an Position III gesetzt werden. Der abschließende Schritt (nicht dargestellt) ist es, das Coverage zu übertragen.
Referenzliste
Maling, D.H. Coordinate Systems and Map Projections. George Philip., 1973.
Maling, D.H. "Coordinate systems and map projections for GIS." In: Maguire D.J., M.F. Goodchild, and D.W. Rhind (eds.), Geographical Information Systems: principles and applications. Vol. 1, S. 135-146. Longman Group UK Ltd., 1991.
Moffitt, F.H., and E.M. Mikhail, Photogrammetry. Dritte Ausgabe. Harper and Row, Inc., 1980.
Pettofrezzo, A.J, Matrices and Transformations. Dover Publications, Inc., 1966.
Slama, C.C., C. Theurer, and S.W. Henriksen (eds.), Manual of Photogrammetry. 4. Auflage. Kapitel XIV, S. 729-731. ASPRS, 1980.