Available with Spatial Analyst license.
The Band Collection Statistics tool provides statistics for the multivariate analysis of a set of raster bands. When using the Compute covariance and correlation matrices option is enabled, the covariance and correlation matrices are output as well as the basic statistical parameters, such as the values of minimum, maximum, mean, and standard deviation for every layer.
The covariance matrix contains values of variances and covariances. The variance is a statistical measure showing how much variance there is from the mean. To calculate these variances, the squares of the differences between each cell value and the mean value of all cells are averaged. The variances for every layer can be read along the diagonal of the covariance matrix moving from the upper left to the lower right. The variances are expressed in cell-value units squared.
The remaining entries within the covariance matrix are the covariances between all pairs of input rasters. The following formula is used to determine the covariance between layers i and j:
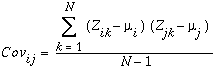
where:
Z - value of a cell
i, j - are layers of a stack
µ - is the mean of a layer
N - is the number of cells
k - denotes a particular cell
The covariance of two layers is the intersection of the appropriate row and column. The covariance between layers 2 and 3 is the same as the covariance between layers 3 and 2. The values of the covariance matrix are dependent on the value units, while the values of the correlation matrix are not.
The correlation matrix shows the values of the correlation coefficients that depict the relationship between two datasets. In the case of a set of raster layers, the correlation matrix presents the cell values from one raster layer as they relate to the cell values of another layer. The correlation between two layers is a measure of dependency between the layers. It is the ratio of the covariance between the two layers divided by the product of their standard deviations. Because it is a ratio, it is a unitless number. The equation to calculate the correlation is as follows:
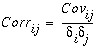
Correlation ranges from +1 to -1. A positive correlation indicates a direct relationship between two layers, such as when the cell values of one layer increase, the cell values of another layer are also likely to increase. A negative correlation means that one variable changes inversely to the other. A correlation of zero means that two layers are independent of one another.
The correlation matrix is symmetrical. Its diagonal from the upper left to lower right is 1.0000 since the correlation coefficient of identical layers is +1.
Example
The example below shows the contents of the output from Band Collection Statistics for a four-layer multiband raster. The first table shows the basic statistics when the Compute matrices option is not used. However, when the option is checked, the covariance and correlation matrices are also calculated. The output statistics contained in the output statistics file are displayed.
Only mean calculated
Output with Compute covariance and correlation matrices disabled (BRIEF):
# STATISTICS of INDIVIDUAL LAYERS
# Layer MIN MAX MEAN STD
# ---------------------------------------------------------------
1 1.0000 21.0000 7.8410 4.1690
2 1.0000 128.0000 25.5144 35.8494
3 296.9573 4073.6306 1565.5359 763.9803
4 0.3333 127.5000 51.5314 29.7958
# ===============================================================Both mean and matrices calculated
Output with Compute covariance and correlation matrices enabled (DETAILED):
# STATISTICS of INDIVIDUAL LAYERS
# Layer MIN MAX MEAN STD
# ---------------------------------------------------------------
1 1.0000 21.0000 7.8410 4.1690
2 1.0000 128.0000 25.5144 35.8494
3 296.9573 4073.6306 1565.5359 763.9803
4 0.3333 127.5000 51.5314 29.7958
# ===============================================================
# COVARIANCE MATRIX
# Layer 1 2 3 4
# ---------------------------------------------------------------
1 17.3826 16.9320 3177.5947 87.9590
2 16.9320 1285.3096 3117.1753 31.3420
3 3177.5947 3117.1753 583723.0625 16137.9785
4 87.9590 31.3420 16137.9785 887.8751
# ===============================================================
# CORRELATION MATRIX
# Layer 1 2 3 4
# ---------------------------------------------------------------
1 1.0000 0.1133 0.9976 0.7080
2 0.1133 1.0000 0.1138 0.0293
3 0.9976 0.1138 1.0000 0.7089
4 0.7080 0.0293 0.7089 1.0000
# ===============================================================References
Snedecor, G. W., and W. G. Cochran. 1968. Statistical Methods, 6th ed. Ames, Iowa: The Iowa State University Press.