Available with 3D Analyst license.
A TIN surface data model is composed of nodes, edges, triangles, hull polygons, and topology.
Nodes
Nodes are the fundamental building blocks of a TIN. The nodes originate from the points and line vertices contained in the input data sources. Every node is incorporated in the TIN triangulation. Every node in the TIN surface model must have a z-value.

Edges
Every node is joined with its nearest neighbors by edges to form triangles, which satisfy the Delaunay criterion. Each edge has two nodes, but a node may have two or more edges. Because edges have a node with a z-value at each end, it is possible to calculate a slope along the edge from one node to the other.
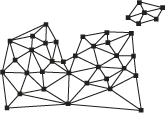
Each feature in the input data sources used to build the TIN is processed in accordance with its surface feature type. Breakline features are always maintained as edges in the TIN triangulation. These breakline TIN edges are flagged internally as either hard or soft edges.
Triangles
Each triangular facet describes the behavior of a portion of the TIN's surface. The x, y, and z coordinate values of a triangle's three nodes can be used to derive information about the facet, such as slope, aspect, surface area, and surface length. Considering the entire set of triangles as a whole, it is possible to derive additional information about the surface, including volume, surface profiles, and visibility analysis.
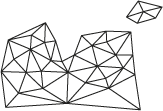
Because each facet summarizes a certain surface behavior, it is important to ensure that the sample points are selected adaptively to give the best possible surface fit. A TIN surface model can yield poor results if important regions of the surface are sampled inadequately.
Hull
The hull of a TIN is formed by one or more polygons containing the entire set of data points used to construct the TIN. The hull polygons define the zone of interpolation of the TIN. Inside or on the edge of the hull polygons, it is possible to interpolate surface z-values, perform analysis, and generate surface displays. Outside the hull polygons, it is not possible to derive information about the surface. The hull of a TIN can be formed by one or more polygons, which can be nonconvex.
A nonconvex hull must be user-defined by including Clip and Erase exclusion features during the construction of the TIN. These features explicitly define the edge of the surface. When no exclusion features are used to define the hull, the TIN generator creates a convex hull to define the bounding edges of the TIN. A convex hull is a polygon with the property that any line connecting any two points of the TIN must itself lie inside or define the edge of the convex hull. The definition of a nonconvex hull is essential to prevent the generation of erroneous information in regions of the TIN outside the actual dataset but inside the convex hull. Consider the diagram below.
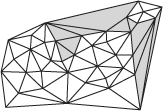
Without the use of clip features, incorrect values may be interpolated in the shaded regions.
Topology
The topological structure of a TIN is defined by maintaining information defining each triangle's nodes, edge numbers, type, and adjacency to other triangles. For each triangle, a TIN records:
- The triangle number
- The numbers of each adjacent triangle
- The three nodes defining the triangle
- The x,y coordinates of each node
- The surface z-value of each node
- The edge type of each triangle edge (hard or soft)
In addition, the TIN maintains a list of all the edges that form the TIN's hull and information defining the TIN's projection and units of measure.
How a TIN is stored
Like a coverage, a TIN is stored as a directory of files. Note, however, that a TIN is not a coverage and has no associated INFO files. A TIN directory consists of seven files containing information about the TIN surface. These files are encoded in binary format and are not readable by standard text display or editing programs.