Geometry

Supported with:
Library dependencies: System, SystemUI

Additional library information: Contents, Object Model Diagram

The Geometry library provides vector representations for points, multipoints, polylines, polygons, and multipatches. Geometries are used by the geodatabase and graphic element systems to define the shapes of features and graphics. They supply operations that are used by the editor and map symbology systems to define and symbolize features. Spatial references describe where these geometries are located on the earth. They also define the resolution and valid values for the coordinates used by these geometries. Almost every system in ArcObjects uses geometries and spatial references in some way.
To use geometries accurately, consistently and predictably, you need to understand how geometries and spatial references work together.
Descriptions and code samples for the majority of objects supplied by the geometry system are also provided in this overview.

See the following sections for more information about this namespace:

Geometry objects
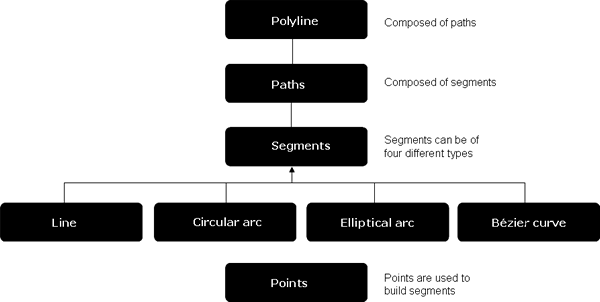
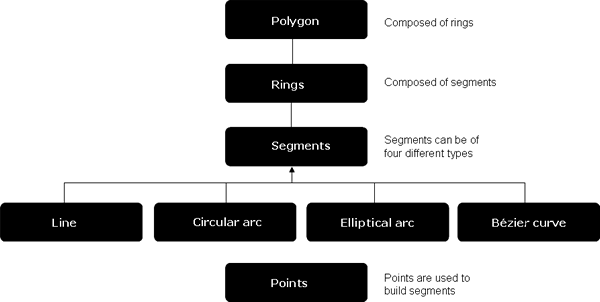
In addition to the top level geometries (points, multipoints, polylines, and polygons), paths, Rings, and segments serve as building blocks for polylines and polygons. Polylines contain paths and polygons contain rings. Paths and rings are sequences of vertices connected by segments. A segment is a parametric function that defines the shape of the curve connecting its vertices. Segment types include CircularArc, Line, EllipticArc, and BézierCurve. In addition to the s,y coordinates for each vertex in a geometry, additional vertex attributes can be defined: m-measure, z-elevation, and ID (foreign key). Envelopes describe the spatial extent of other geometries, and GeometryBags provide operations on collections of geometries. Geometry objects are not meant to be extended by developers.
Multipoint, polyline, and polygon geometries have constraints on their shapes. For example, a polygon must have its interior clearly defined and separated from its exterior. When all constraints are satisfied, a geometry is referred to as simple. When a constraint is violated, or it is not known if the constraint is met, the geometry is referred to as non-simple. The ITopologicalOperator, IPolygonN, and IPolylineN interfaces provide operations for testing and enforcing simplicity. The software development kit (SDK) documentation for the Simplify method of the ITopologicalOperator describes these rules.
Each vertex of a geometry, in addition to its x,y coordinates, can optionally have additional attributes, called vertex attributes. The z-vertex attribute is a double precision value that can be used to represent heights or depths relative to a vertical coordinate system. The m-vertex attribute, also called a measure, is a double precision value that can be used to establish a linear reference system on a geometry (usually a polyline), such as the exits along a highway. The ID vertex attribute, also called a point ID, is a signed integer that can be used as a foreign database key to associate additional information with each vertex such as survey measurements.
Vertex attributes can be added to or removed from any geometry at any time and in any combination. For example, a polyline can originate with no vertex attributes, have z attributes added, IDs added, and z attributes removed. When a geometry is aware of its vertex attributes, those attributes will be persisted as part of the geometry, and will be included in the output of topological operations that involve that geometry. If a geometry is not aware of its attributes, those attributes will be ignored when the geometry is persisted and the attributes will not appear in the output of a topological operation involving that geometry. The attribute awareness of a geometry is controlled by one of the interfaces IZAware, IMAware, and IPointIDAware. The attribute values are not removed from a geometry if its awareness is disabled. One of the polyline examples in this topic illustrates use of the point ID attribute.
Geometries, especially the segment types, have a set of methods for defining their location. For example, the IConstructCircularArc interface shows the different ways a circular arc segment can be defined. Typically, interfaces or methods that include the word Construct in their name use a set of input parameters (including other geometries) to define the target geometry. The inputs are not altered.
Top level geometries support the classical set-theoretic operations for generating new geometries including union, intersection, difference, and symmetric difference. These operations are exposed on the ITopologicalOperator interface and usually operate on a pair of geometries at a time. ITopologicalOperator.ConstructUnion can operate on more than two. New geometries are created to represent the results. Top level geometries also support the IRelationalOperator interface, which can perform a variety of tests on a pair of geometries such as disjoint, contains, and touches.
Both of these interfaces use the spatial reference associated with the input geometries when determining the answer. Two important properties of a spatial reference are its coordinate grid and its x,y tolerance. Different values for these properties can cause the relational and topological operators to produce different results.

Geometry environment

Geometry enviroment provides a way of creating geometries from different inputs and setting or getting global variables for controlling the behavior of geometry methods. It also provides Java friendly versions of methods originally defined on other geometry objects (see the IGeometryBridge and IGeometryBridge2 interfaces). The GeometryEnvironment object is a singleton object; therefore, calling new several times doesn't create a new object each time—instead, it returns a reference to the existing GeometryEnvironment.

Using the geometry and spatial reference environments

The following code example uses the IGeometryBridge2 interface on the GeometryEnvironment singleton object to define a polyline from an array of WKSPoint structures. It also uses the SpatialReferenceEnvironment singleton object to create a predefined projected coordinate system. Some of the previous concepts discussed are used in this code example.
[Java] 
public static void geometryEnvironmentTest()throws IOException{
    GeometryEnvironment geomEnvironment = new GeometryEnvironment();
    SpatialReferenceEnvironment spatialReferenceFactory = new
        SpatialReferenceEnvironment();
    Polyline polyline = new Polyline();
    // Create a projected coordinate system and define its domain, resolution, and x,y tolerance.
    ProjectedCoordinateSystem coordinateSystem = (ProjectedCoordinateSystem)
        spatialReferenceFactory.createProjectedCoordinateSystem
        (esriSRProjCSType.esriSRProjCS_NAD1983UTM_11N);
    coordinateSystem.constructFromHorizon();
    coordinateSystem.setDefaultXYTolerance();
    polyline.setSpatialReferenceByRef(coordinateSystem);
    // Create an array of WKSPoint structures starting in the middle of the x,y domain of the 
    // projected coordinate system.
    double[] xmin = new double[1];
    double[] xmax = new double[1];
    double[] ymin = new double[1];
    double[] ymax = new double[1];
    coordinateSystem.getDomain(xmin, xmax, ymin, ymax);
    _WKSPoint m = new _WKSPoint();
    m.x = (xmin[0] + xmax[0]) * 0.5;
    m.y = (ymin[0] + ymax[0]) * 0.5;
    _WKSPoint[] wksPoints = new _WKSPoint[10];
    for (int i = 0; i < wksPoints.length; i++){
        wksPoints[i] = new _WKSPoint();
        wksPoints[i].x = m.x + i;
        wksPoints[i].y = m.y + i;
    }
    geomEnvironment.addWKSPoints(polyline, wksPoints);
}

Envelope

For many applications, the coordinates of a geometry are treated as existing in a planar (Cartesian) coordinate space. An envelope is a rectangle with sides parallel to that space defining the spatial extent of a geometry. It can also describe the extent of the geometry's z-, ID-, and m-vertex attributes. You can obtain (copies of) envelopes of other geometries or create envelopes directly. In the first case, the spatial reference of the envelope is the spatial reference of its defining geometry.
The following code example determines the spatial extent of the union of two geometries:
[Java] 
Envelope env1 = (Envelope)feat1.getShape().getEnvelope();
System.out.println(env1.getXMin() + " " + env1.getYMin() + " " + env1.getXMax() + 
    " " + env1.getYMax());
Envelope env2 = (Envelope)feat2.getShape().getEnvelope();
env1.union(env2);
System.out.println(env1.getXMin() + " " + env1.getYMin() + " " + env1.getXMax() + 
    " " + env1.getYMax());

Geometry bag

Geometry bag is a set of references to other geometry objects supporting the IGeometry interface. Objects of any level (segments, polylines, or polygons) can be added to the GeometryBag via the IGeometryCollection interface. However, placing objects of different geometry types may not be suitable when using GeometryBag in some topological operations. For example, a GeometryBag must contain strictly polygons, polylines, or envelopes when using it as a parameter to the ITopologicalOperator.constructUnion.
Like other geometries, a geometry bag has a spatial reference property. A geometry added to a bag will reference the same spatial reference as the bag. If the bag has no spatial reference, neither will the geometry after it is added to the bag (this is usually an error). Define the spatial reference of the bag before adding geometries to it.

Creating the union of several polygons

The following code example constructs a polygon representing the topological union of several polygons. The source polygons come from a feature class. References to the polygons are inserted into a geometry bag. The geometry bag is used as the input parameter to the ConstructUnion method. The spatial reference of the geometry bag is defined before adding geometries to it.
[Java] 
//Set the properties of the spatial filter.
SpatialFilter qfilter = new SpatialFilter();
qfilter.setGeometryByRef(fclass.getExtent());
GeometryBag geometryBag = new GeometryBag();
geometryBag.setSpatialReferenceByRef(fclass.getSpatialReference());
FeatureCursor fcursor = new FeatureCursor(fclass.search(qfilter, false));
Feature feat = (Feature)fcursor.nextFeature();
while (feat != null){
    geometryBag.addGeometry(feat.getShape(), null, null); 
        //Add a reference to this feature’s geometry into the bag
    feat = (Feature)fcursor.nextFeature();
}

// Create the polygon that will be the union of the features returned from the search cursor.
// The spatial reference of this feature does not need to be set ahead of time. 
// The ConstructUnion method defines the constructed polygon’s spatial reference to be the same as 
// the input geometry bag.
Polygon polygon = new Polygon();
polygon.constructUnion(geometryBag);
System.out.println(polygon.getGeometryCount());

Transformations

The transformation objects can be used to apply various linear coordinate transformations to top-level geometries (points, multipoints, polylines, and polygons). Typically, you create a particular kind of transformation object, define its properties, and pass it to the geometry being transformed to perform the transform on that geometry. Occasionally, you need to extract the points from the geometry and transform them or transform arrays of WKSPoints. The following are the transformation types:

Using an affine transformation

The following code example uses an affine transformation to transform a digitized geometry into ground (projected) coordinates. The same transformation is then applied to an array of double precision raw coordinate values. You may be interested in the latter approach when transforming large numbers of coordinates coming from a text file, binary file, or another large source of raw coordinates. This avoids the processing overhead of creating COM point objects for every coordinate. See the following code example:
[Java] 
public static void affineTransformation2DExample()throws IOException{
    ShapefileWorkspaceFactory shapefileWorkspaceFactory = new
        ShapefileWorkspaceFactory();
    Workspace wksp = new Workspace(shapefileWorkspaceFactory.openFromFile(
        "C:/Program Files/ArcGIS/java/samples/data/usa", 0));
    FeatureClass fclass = new FeatureClass(wksp.openFeatureClass("states.shp"));
    SpatialFilter qfilter = new SpatialFilter();
    qfilter.setGeometryByRef(fclass.getExtent());
    GeometryBag geometryBag = new GeometryBag();
    geometryBag.setSpatialReferenceByRef(fclass.getSpatialReference());
    FeatureCursor fcursor = new FeatureCursor(fclass.search(qfilter, false));
    Feature feat = (Feature)fcursor.nextFeature();
    Polygon poly = (Polygon)feat.getShape();
    //Sample.
    Point[] digitizerPoints = new Point[10]; 
        //Get the digitizer control point values from somewhere
    Point[] groundPoints = new Point[10]; 
        // Get the ground control coordinate values from somewhere 
    // (aGroundPoints(i) is the ground point corresponding to aDigitizerPoints(i).
    //Boilerplate.
    int i = 0;
    for (i = 0; i < poly.getPointCount() && i < 10; i++){
        groundPoints[i] = (Point)poly.getPoint(i);
    }
    for (i = 10; i < poly.getPointCount() && i < 20; i++){
        digitizerPoints[i] = (Point)poly.getPoint(i);
    }

    //Sample.
    AffineTransformation2D transformation = new AffineTransformation2D();
    transformation.defineFromControlPoints(10, digitizerPoints[0], groundPoints[0]);
    double[] fromToRMS = new double[1];
    double[] toFromRMS = new double[1];
    transformation.getRMSError(fromToRMS, toFromRMS);
    if (fromToRMS[0] > 0.05){
        System.out.println(
            "RMS error is too large; please redigitize control points");
        return ;
    }
    Polygon digitizedGeometry = poly; 
        //Get geometry to be transformed from digitizer input
    //pTransformee.Transform esriTransformForward, pAff2D
    digitizedGeometry.transform(esriTransformDirection.esriTransformForward,
        transformation);
    //pDigitizedGeometry is now in the destination coordinate system and should be assigned a 
    //spatial reference.
    //   
    //Apply the same transformation directly to an array of double precision values 
    //representing (x,y) points.
    //The x,y values are assumed to be interleaved in the array: aFromPoints(1) is the x coordinate 
    //for the first point, aFromPoints(2) is the y coordinate, and so on.
    double[] fromPoints = new double[50];
    double[][] toPoints = new double[1][50];
    //fromPoints reads array of points from a file.

    transformation.transformPointsFF(esriTransformDirection.esriTransformForward,
        fromPoints, toPoints);
}

Points

A two dimensional point, optionally with measure (M), height (Z), and ID attributes.

Snapping a point to a coordinate grid

The following example creates a point, associates it with the spatial reference of a feature class, positions it in the center of the domain of the spatial reference, and snaps its coordinates to the spatial reference's coordinate grid:
[Java] 
ISpatialReference spRef = fclass.getSpatialReference();
double[] xmin = new double[1];
double[] ymin = new double[1];
double[] xmax = new double[1];
double[] ymax = new double[1];
spRef.getDomain(xmin, xmax, ymin, ymax);
Point point = new Point();
point.setSpatialReferenceByRef(spRef);
point.setX((xmin[0] + xmax[0]) * 0.5);
point.setY((ymin[0] + ymax[0]) * 0.5);
System.out.println("Before snapping: " + point.getX() + point.getY());
point.snapToSpatialReference();
System.out.println("After snapping: " + point.getX() + point.getY());

Multipoints

A multipoint is an ordered collection of points; optionally has measure (m), height (z), and ID attributes.The IPointCollection interface implemented by a multipoint object provides direct access to its point elements. This is different than how IPointCollection behaves when that interface is used to provide access to the vertices of a polyline or polygon. In that case, you are working with copies of the points.

Creating a multipoint object from the vertices of a polyline

The following code example creates a multipoint with point elements being copies of the vertices of an existing polyline. It offsets those elements five units to the right using one transformation method, then offsets them up another five units.
[Java] 
//Set the properties of the spatial filter.
SpatialFilter qfilter = new SpatialFilter();
qfilter.setGeometryByRef(fclass.getExtent());
qfilter.setSpatialRel(esriSpatialRelEnum.esriSpatialRelContains);
qfilter.setGeometryField(fclass.getShapeFieldName());

GeometryBag geometryBag = new GeometryBag();
geometryBag.setSpatialReferenceByRef(fclass.getSpatialReference());
FeatureCursor fcursor = new FeatureCursor(fclass.search(qfilter, false));
Feature feat = new Feature(fcursor.nextFeature());
Polyline polyline = (Polyline)feat.getShape();
Multipoint multipoint = new Multipoint();
multipoint.setSpatialReferenceByRef(polyline.getSpatialReference());
multipoint.addPointCollection(polyline);
AffineTransformation2D shiftBy5 = new AffineTransformation2D();
shiftBy5.move(5, 0);
multipoint.transform(esriTransformDirection.esriTransformForward, shiftBy5);
multipoint.move(0, 5);
multipoint.transform(esriTransformDirection.esriTransformForward, shiftBy5);

Polylines

A polyline is an ordered collection of paths; optionally has measure (m), height (z), and ID attributes. The IPointCollection interface on a polyline manipulates copies of its vertices. Use the IGeometryCollection interface to directly access its paths and the ISegmentCollection interface to directly access its segments. IPointCollection and ISegmentCollection interfaces are also available on path objects and are characterized the same way. See the following illustration of a polyline's structure:

Creating a multipart polyline

In the following illustration, the input polyline is shown in the background and the new polyline is shown in dark green with its vertices marked. Each part of the new polyline is a single segment normal to a segment from the original polyline, incident at its midpoint, and 1/3 its length:
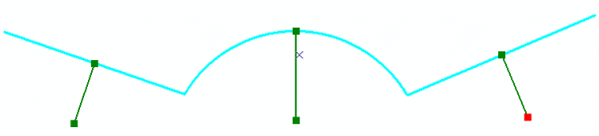
The following code example uses an existing polyline to define a new multipart polyline:
[Java] 
Polyline newPolyline = new Polyline();
newPolyline.setSpatialReferenceByRef(polyline.getSpatialReference()); 
    //Always associate new top level geometries with an appropriate spatial reference.
IEnumSegment polylineSegments = polyline.getEnumSegments();
ISegment[] segment = new ISegment[1];
int[] partIndex = new int[1];
int[] segmentIndex = new int[1];
// Iterate over existing polyline segments using a segment enumerator.
polylineSegments.next(segment, partIndex, segmentIndex);
while (segment[0] != null){
    Line line = new Line();
    // Geometry methods with _Query_ in their name expect to modify existing geometries. 
    // In this case, the QueryNormal method modifies an existing line segment (line) to be the normal vector to 
    // segment at the specified location along the segment.
    segment[0].queryNormal(esriSegmentExtension.esriNoExtension, 0.5, true,
        segment[0].getLength() / 3, line);
    Path path = new Path(); 
        //Since each normal vector is not connected to others, create a new path for each one.
    path.addSegment(line, null, null);
    newPolyline.addGeometry(path, null, null); 
        //The spatial reference associated with pNewG will be assigned to all incoming paths and segments.
    polylineSegments.next(segment, partIndex, segmentIndex);
}

// newPolyline now contains the new, multipart polyline.

Adding point IDs to a polyline

The following code example shows how to make an existing polyline point ID aware and define ID values for each of its vertices. The code example assumes that an edit session exists on the workspace containing the feature class whose features are being iterated over.
[Java] 
FeatureCursor fcursor = new FeatureCursor(fclass.search(null, false));
IFeature ifeat = fcursor.nextFeature();
while (ifeat != null){
    Polyline polyline = (Polyline)ifeat.getShape();
    polyline.setPointIDAware(true); 
        //The polyline is now point ID aware. It will persist its point IDs the next time it is saved.
    IEnumSegment segments = polyline.getEnumSegments();
    //ISegment[] segment = new ISegment[1];
    Line[] segment = new Line[1];
    int[] partIndex = new int[1];
    int[] segmentIndex = new int[1];
    segments.next(segment, partIndex, segmentIndex);
    while (segment[0] != null){
        segment[0].setIDs(segmentIndex[0], segmentIndex[0] + 1);
        segments.next(segment, partIndex, segmentIndex);
    }
    ifeat.setShapeByRef(polyline);
    ifeat.store();
    ifeat = fcursor.nextFeature();
}

//featureWksp.stopEditOperation();
featureWksp.stopEditing(true);

Polygons

Polygons are a collection of rings ordered by their containment relationship; optionally has measure (m), height (z), and ID attributes. Each ring is a collection of segments. The IPointCollection interface on polygons and rings manipulates copies of vertices. Use the IGeometryCollection and ISegmentCollection interfaces to access rings and segments directly. See the following illustration of a polygon's structure:

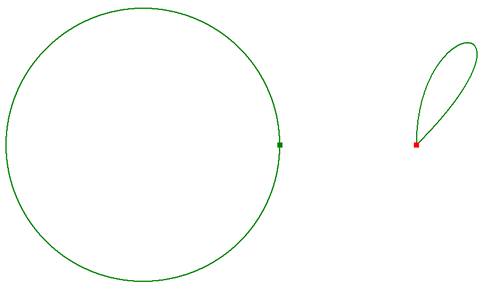
Building a polygon using segments and points

The following builds two multipart polygons in two different ways. The first polygon is built segment by segment. The second is built by defining its vertices as an array of WKSPoint structures. The first approach gives you the most control if you are using advanced construction techniques or curved segments (circular arcs, Bézier curves, and so on). The second approach is recommended for efficiently building polygons from bulk coordinate data that have vertices connected with straight lines only. The techniques shown here can also be applied to polyline construction. See the following illustration:
See the following code example:
[Java] 
private static double PI = 3.14159265358979;

public static void constructPolygons()throws IOException{
    //Boilerplate. 
    SdeWorkspaceFactory sdeWorkspaceFactory = new SdeWorkspaceFactory();
    PropertySet pset = new PropertySet();
    pset.setProperty("SERVER", "hemlock");
    pset.setProperty("INSTANCE", "9210");
    pset.setProperty("USER", "gdb");
    pset.setProperty("PASSWORD", "gdb");
    pset.setProperty("VERSION", "sde.DEFAULT");
    Workspace featureWksp = new Workspace(sdeWorkspaceFactory.open(pset, 0));
    featureWksp.startEditing(false);
    //featureWksp.startEditOperation();
    FeatureClass fclass = new FeatureClass(featureWksp.openFeatureClass("GDB.Roads"))
        ;
    System.out.println("FeatureClass name = " + fclass.getName());
    FeatureCursor fcursor = new FeatureCursor(fclass.search(null, false));
    IFeature ifeat = fcursor.nextFeature();
    ISpatialReference spref = ifeat.getShape().getSpatialReference();
    //Sample.
    Polygon polygon = new Polygon();
    polygon.setSpatialReferenceByRef(spref); 
        //Always define the spatial reference of new top level geometries.
    // Create the segments and rings. If this were a single part polygon, you can add
    // segments directly to the polygon and it creates the ring internally.
    // You cannot reuse the same ring object. When rings are added to the polygon, 
    // it takes ownership of them. You cannot reuse a ring for building another polygon. 
    // These same restrictions also apply to segments.
    CircularArc arc = new CircularArc();
    B � �zierCurve curve = new B � �zierCurve();
    Ring ring1 = new Ring();
    Ring ring2 = new Ring();
    ring1.addSegment(arc, null, null);
    ring2.addSegment(curve, null, null);
    polygon.addGeometry(ring1, null, null);
    polygon.addGeometry(ring2, null, null);
    // At this point, you have constructed a _shell_ geometry. It consists of one 
    // polygon containing two rings, each of which contains one segment. 
    // However, the coordinates of those segments have not been defined. 
    // Because you still have references to those segments, define their 
    // coordinates now.
    Point point = new Point();
    point.setX( - 10);
    point.setY(0);
    arc.putCoordsByAngle(point, 0, 2 * PI, 10);
    Point[] controlPoints = new Point[4];
    for (int i = 0; i < 4; i++){
        controlPoints[i] = new Point();
    }
    controlPoints[0].setX(10);
    controlPoints[0].setY(0);
    controlPoints[1].setX(10);
    controlPoints[1].setY(10);
    controlPoints[2].setX(20);
    controlPoints[2].setY(10);
    controlPoints[3].setX(10);
    controlPoints[3].setY(0);

    curve.putCoords(controlPoints);
    // pPolygon has now been defined. When changing segment coordinates directly 
    // be careful to let the top level geometry know that things have changed
    // underneath it, so that it can delete any cached properties 
    // that it might be maintaining, such as envelope, length, area, and so on.
    //
    // When you use certain methods on the top-level geometry implementation 
    // of IGeometryCollection interface, like AddGeometry, it will automatically
    // invalidate any cached properties.
    polygon.geometriesChanged();
    // Build another polygon from a bunch of points. As before, assume that 
    // two parts (rings) need to be created. If the polygon was single part, 
    // add the points directly to the polygon without creating a ring.
    //      
    // At ArcGIS 9.2, the recommended way to add arrays of points to a geometry is to use 
    // the IGeometryBridge2 interface on the GeometryEnvironment singleton object.
    GeometryEnvironment gBridge = new GeometryEnvironment();
    Polygon pointPolygon = new Polygon();
    pointPolygon.setSpatialReferenceByRef(spref); 
        //Define the spatial reference of the new polygon.
    Ring r1 = new Ring();
    int cPoints1 = ring1.getPointCount(); //The number of points in the first part.
    _WKSPoint[][] wksPointBuffer = new _WKSPoint[1][cPoints1];
    for (int i = 0; i < cPoints1; i++)
        wksPointBuffer[0][i] = new _WKSPoint();

    gBridge.queryWKSPoints(ring1, cPoints1, wksPointBuffer); 
        //Read cPoints1 into the point buffer.
    gBridge.setWKSPoints(r1, wksPointBuffer[0]);
    Ring r2 = new Ring();
    int cPoints2 = ring2.getPointCount(); //The number of points in the first part.
    wksPointBuffer = new _WKSPoint[1][cPoints2];
    for (int i = 0; i < cPoints2; i++)
        wksPointBuffer[0][i] = new _WKSPoint();
    gBridge.queryWKSPoints(ring2, cPoints2, wksPointBuffer); 
        //Read cPoints2 into the point buffer.
    gBridge.setWKSPoints(r2, wksPointBuffer[0]);
    pointPolygon.addGeometry(r1, null, null);
    pointPolygon.addGeometry(r2, null, null);
    // pPointPoly is defined.
}

Multipatch

The MultiPatch geometry type was developed to address the needs for a 3D polygon geometry type—unconstrained by 2D validity rules. Without eliminating the constraints that rule out vertical walls, for example, representing extruded 2D lines and footprint-polygons for 3D visualization would not be possible. Besides eliminating 2D constraints, multipatches provide better control over polygon face orientations, and a better definition of polygon face interiors.
Multipatches have also been extended to provide advanced geometric representations for 3D features. These complex 3D objects can be part of a synthetic landscape model stored in a geodatabase. The target of these extensions is improved visualization quality.
One key capability is that of supporting per-vertex normals that improve the quality of shading under illumination. Another key capability is that of precise image/texture mapping on to the MultiPatch geometry, via explicit texture coordinates. The geometry of a multipatch is inline with a GeometryMaterialList, which contains one or more GeometryMaterials. These GeometryMaterials can be a color, a texture (image), or both. The new class for this functionality is GeneralMultiPatchCreator, which is used to construct a MultiPatch.
The following illustration shows a relationship between objects used in multipatch construction:
MultiPatch OMD excerpt
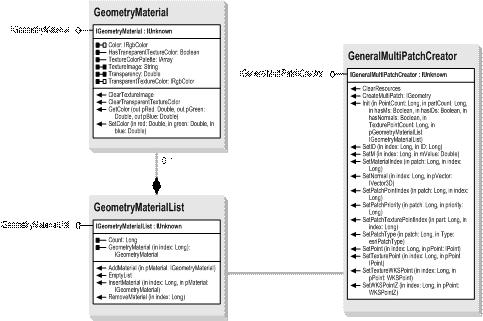
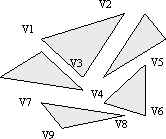
Another key improvement to multipatches is the support of the triangles part. This extends the original multipatch parts (triangle strip, triangle fan, outer ring, inner ring, first ring, and ring). The triangles part completes the range of vertex-based part types and facilitates capturing the output results of different triangle-mesh tessellators or 3D object importers (for example, from 3D studio models), which contain triangles that are not connected, into a multipatch geometry. Developers can also make use of the triangles part as a useful addition to the initial multipatch part types offered.
A single triangles part represents a collection of triangular faces. Each consecutive triplet of vertices defines a new triangle. The size of a triangles part must be a multiple of three. See the following illustration:
Triangles illustrationt

See the following regarding the use of rings and multipatch geometries:
To construct a textured multipatch geometry, use the IGeneralMultiPatchCreator interface even though the IEncode3DProperties interface that includes the PackTexture2D method still works. With the introduction of explicit vertex normals and texture coordinates, the usage of IEncode3DProperties is now deprecated.
The following code example shows a simple example of constructing a textured multipatch geometry using a TriangleStrip that resembles a vertical polygon, assuming it is 300 (width) x 100 (height) in size.
[Java] 
//Prepare the geometry material list.
GeometryMaterial texture = new GeometryMaterial();
texture.setTextureImage("C:/Temp/MyImage.bmp");
GeometryMaterialList materialList = new GeometryMaterialList();
materialList.addMaterial(texture);
//Create the multipatch.
GeneralMultiPatchCreator mpCreator = new GeneralMultiPatchCreator();
mpCreator.init(4, 1, false, false, false, 4, materialList);
// Set the texture coordinates for a panel.
_WKSPoint txLL = new _WKSPoint();
txLL.x = 0;
txLL.y = 1;
_WKSPoint txLR = new _WKSPoint();
txLR.x = 1;
txLR.y = 1;
_WKSPoint txUR = new _WKSPoint();
txUR.x = 1;
txUR.y = 0;
_WKSPoint txUL = new _WKSPoint();
txUL.x = 0;
txUL.y = 0;
_WKSPointZ pUL = new _WKSPointZ();
pUL.x = 0;
pUL.y = 0;
pUL.z = 0;
_WKSPointZ pUR = new _WKSPointZ();
pUR.x = 300;
pUR.y = 0;
pUR.z = 0;
_WKSPointZ pLL = new _WKSPointZ();
pLL.x = 0;
pLL.y = 0;
pLL.z =  - 1 * 100;
_WKSPointZ pLR = new _WKSPointZ();
pLR.x = 300;
pLR.y = 0;
pLR.z =  - 1 * 100;
// Set up part.
mpCreator.setPatchType(0, esriPatchType.esriPatchTypeTriangleStrip); 
    //Could also use a ring or a triangle fan.
mpCreator.setMaterialIndex(0, 0);
mpCreator.setPatchPointIndex(0, 0);
mpCreator.setPatchTexturePointIndex(0, 0);
// Set real world points.
mpCreator.setWKSPointZ(0, pUR);
mpCreator.setWKSPointZ(1, pLR);
mpCreator.setWKSPointZ(2, pUL);
mpCreator.setWKSPointZ(3, pLL);
//Set texture points.
mpCreator.setTextureWKSPoint(0, txUR);
mpCreator.setTextureWKSPoint(1, txLR);
mpCreator.setTextureWKSPoint(2, txUL);
mpCreator.setTextureWKSPoint(3, txLL);
MultiPatch mpatch = new MultiPatch();
mpatch = (MultiPatch)mpCreator.createMultiPatch();
}

Spatial reference objects
Geometries are georeferenced through a spatial reference. A spatial reference includes the coordinate system and several coordinate grids. A coordinate system includes information, such as the unit of measure, earth model used, and sometimes how the data was projected. The coordinate grids define the x,y, z, and m resolution values, the corresponding domain extents and a set of tolerance values. A geometry's coordinates (or vertex attributes) must fall within the domain extent and be rounded to the resolution. The tolerance values are used by geometric operations that relate coordinates or compute new ones.
X,y values can be georeferenced with a geographic or projected coordinate system. A geographic coordinate system (GCS) is defined by a datum, an angular unit of measure, usually either degrees or grads, and a prime meridian. A projected coordinate system (PCS) consists of a linear unit of measure, usually meters or feet, a map projection, the specific parameters used by the map projection, and a geographic coordinate system. A PCS or GCS can have a vertical coordinate system as an optional property. A vertical coordinate system (VCS) georeferences z-values. A VCS includes a geodetic or vertical datum, a linear unit of measure, an axis direction, and a vertical shift. M-measure values do not have a coordinate system.
A spatial reference that includes an unknown coordinate system (UCS) only includes a grid (domain extent) and a tolerance. It is not possible to georeference a geometry associated with a UCS. If at all possible, do not use a UCS. When a GCS or PCS is used, appropriate default x,y domain extent, resolution, and tolerance values can be calculated. All grid and tolerance information for coordinates and attributes are associated with the PCS, GCS, or UCS. A VCS georeferences z-coordinates but does not have a well-defined default grid.
The resolution and domain extent values determine how a geometry is stored. Resolution values are in the same units as the associated coordinate system. For example, if a spatial reference is using a projected coordinate system with units of meters, the x,y resolution value is defined in meters. For many applications, a resolution value of 0.0001 meters (1/10 mm) is appropriate. Use a resolution value that is at least 10 times smaller than the accuracy of the data. If a coordinate system is unknown, or for m-attributes, you will have to set appropriate resolution values according to the data without knowing the unit of measure. In addition, the resolution and domain extent values defining the grid of a spatial reference can affect how a geometry is stored in an ESRI geodatabase, or an ESRI supported file data source. For example, coordinates in an ArcSDE hosted layer are snapped to the integer grid defined by the resolution and domain extent. See the following code example:
[Java] 
Persisted coordinate = IPart((map coordinate � � � minimum domain extent) /
    resolution)(1)
In the preceding code example, the left side of the equation is the integer value that gets stored in the layer. IPart is a function that extracts the integer portion of the real valued result of the equation. The inverse of this operation is used to recreate map coordinates from those data sources that store coordinates as integers.
In addition to the integerization of map coordinates, ArcSDE and file geodatabases compress the resulting integer coordinates by removing leading zeroes (among a few other items). Coordinates with large numeric values after integerization don't compress as well as those with smaller numeric values; therefore, coordinates clustered near the upper-right corner of the domain extent, will not compress as well as those near the lower-left, or minimum domain extent.
Personal geodatabases persist their coordinates as double precision floating point values, but the values have equations applied to them and have been snapped. Shapefiles also persist double precision values, but they are not snapped to the spatial reference grids.
If you've worked with geometries prior to ArcGIS 9.2, the resolution values are the inverse of the precision values. The precision values are also known as the x,y-units, z-units, and m-units, or the scale factor. At ArcGIS 9.2, the terms resolution and precision are treated as synonyms. There may be parts of the application programming interface (API) or documentation that refers to precision or scale factor when it should use the term resolution. The word precision is also used to describe a spatial reference with an enhanced grid.
The coordinate values of a geometry must fall within the appropriate x,y-, z-, and m-domain extents. The largest legal map coordinate value is the upper-right of the domain extent. This coordinate value must also be represented as an integer. The domain extents and resolution values are connected. Together, they form a grid mesh with the resolution defining the mesh separation or cell size. Internally, the resolution and domain extents are used to define an integer grid.
At ArcGIS 9.1 and before, each integer coordinate was allotted 31 bits. At ArcGIS 9.2, 53 bits are provided for data sources created and managed by ArcGIS 9.2. Thus, for a given resolution, the domain extent can be much larger, or alternatively, for a given domain extent, the resolution can be much smaller than is possible for data using a low precision spatial reference. A data source that stores 53 bit coordinates is always associated with a high precision spatial reference. Existing data sets that have not had their spatial references upgraded, are always associated with low precision spatial references.
As an example, if the minimum domain value is 0 and the resolution is 1, the maximum domain value for a high precision data source is 9007199254740990 or 253–2. If the resolution is 0.0001, the maximum domain value is 900719925474.0990. These values are for high precision spatial references, which are new at ArcGIS 9.2. Prior to this release, spatial references were what we now call low precision. A low precision spatial reference uses maximum domain values of 2147483647 or 231–1. If the same resolution value of 0.0001 and a minimum domain extent of zero are used, the largest value that a geometry could have is 214748.3647. This is too small for many projected coordinate systems—universal transverse Mercator (UTM) and state plane. When you have to work with low precision spatial references, carefully balance the tradeoff between domain extent and the resolution or precision values.
If possible, always work with high precision spatial references. By default, when using ArcGIS 9.2, a new spatial reference is high precision. If you are editing or creating data for a geodatabase (of any type) that has not had its spatial reference upgraded, continue to work with low precision spatial references. New Component Object Model (COM) interfaces are available on the various spatial reference objects to determine whether one is low or high precision. A new interface is provided on the SpatialReferenceEnvironment object to convert between high and low precision spatial references using certain assumptions.
In addition to the resolution and domain extent properties of a spatial reference's coordinate grid, the x,y tolerance property is also important. The x,y tolerance is applied to x,y coordinates during relational and topological operations. The x,y tolerance property of a spatial reference describes how far a point is allowed to move in the x,y plane whenever it is necessary to determine if two points are the same. The minimum allowable tolerance value is twice the resolution (or 2.0/scale factor). The z-tolerance property is used when validating topologies in a geodatabase. Different tolerance values can produce different answers for relational and topological operations. For example, two geometries can be classified as disjoint (no points in common) with the minimum tolerance, but a larger tolerance can cause them to be classified as touching.
To achieve precise and predictable results using the geometry library, it is essential that the spatial reference of geometries within a workflow is well defined. When performing a spatial operation using two or more geometries, for example, an intersection, the coordinate systems of the two geometries must be equal. If the coordinate systems of the geometries are different or undefined, the operation could produce unexpected results. Prior to ArcGIS 9.2, the resolution (precision) determined the tolerance value used in a geometry operation. Now, a spatial reference should have explicitly defined tolerance values. In two at a time geometry operations, such as the methods found in the IRelationalOperator and ITopologicalOperator interfaces, the tolerance value of the left operand geometry is used. If the tolerance property of the spatial reference is undefined or there is no spatial reference associated with a geometry, a default grid guaranteed to contain the operands and the minimum allowable tolerance based on the grid are used.
The spatial reference is not defined when creating a new instance of a geometry. It is the developer's responsibility to define a spatial reference that makes sense for the geometry and for the operation. If an existing geometry is coming from a feature class, usually the spatial reference is well defined and the geometry can be used directly or projected without problems.

Spatial reference environment

SpatialReferenceEnvironment is a singleton object used for creating, loading, and storing entire spatial references. Spatial references are often cloned and copied internally. Setting up the SpatialReferenceEnvironment as a singleton object conserves resources and makes it less likely that a spatial reference is deleted completely before it is no longer in use. The SpatialReferenceEnvironment can also create predefined components used for building spatial references (projections, datums, prime meridians, and so on). Finally, you can use it to convert between low and high precision spatial references.

Using ISpatialReferenceFactory to create a predefined spatial reference system

ArcObjects includes a vast array of predefined spatial reference systems and building blocks for spatial reference systems. Each predefined object is identified by a factory code. Factory codes are defined enumeration sets that begin with esriSR. Use the enumeration macro rather than the integer value it represents. Occasionally, the code value for which an enumeration stands changes. This is because many of the values are from the European Petroleum Survey Group (EPSG), which is becoming an industry standard.
The following code example shows how to create predefined spatial reference objects and use them as input to geodatabase operations:
[Java] 
SpatialReferenceEnvironment spfactory = new SpatialReferenceEnvironment();
ProjectedCoordinateSystem pcoordsys = new ProjectedCoordinateSystem();
spfactory.createProjectedCoordinateSystem
    (esriSRProjCSType.esriSRProjCS_WGS1984UTM_11N);
The ISpatialReferenceFactory interface provides methods that use the FactoryCode to generate predefined factory spatial reference objects. The following are the types of functions on this interface:
For example, the createGeographicCoordinateSystem function takes as its only parameter an integer that represents the FactoryCode of a predefined geographic coordinate system. The function returns a fully instantiated GCS object that can be queried for its properties and classes.
Thousands of coordinate system related objects are available through macros. The enumerations all begin with esriSR. Use the enumeration macro rather than the integer value it represents. Many of the FactoryCode values are based on an external standard and the values may change.
The next type of function on the ISpatialReferenceFactory interface returns a complete set of objects. For example, the following code example shows how the createPredefinedProjections function returns a set that contains all the available projection objects. The set is iterated through and the name of each projection with the set is obtained. These type of functions are useful for developers who want to populate a selection list of available SpatialReference objects.
[Java] 
SpatialReferenceEnvironment spfactory1 = new SpatialReferenceEnvironment();
Set projectionSet = (Set)spfactory1.createPredefinedProjections();
System.out.println(projectionSet.getCount());
projectionSet.reset();
for (int i = 0; i < projectionSet.getCount(); i++){
    IProjection projection = (IProjection)projectionSet.next();
    System.out.println(projection.getName());
}
The third type of function supported by ISpatialReferenceFactory deals with PRJ files and strings—createESRISpatialReferenceFromPRJFile takes an old or new style PRJ file and creates a geographic or projected coordinate system from it, depending on the file contents.
The old style PRJ is used with coverages, triangulated irregular networks (TINs), and grids—createESRISpatialReferenceFromPRJ is used to create a spatial reference based on the string buffer of an old style PRJ file. While createESRISpatialReference is similar, the string buffer must be in the format of a new PRJ file. 
The following code example shows how to create a SpatialReference coordinate system directly from a PRJ file (both old and new style files are supported):
[Java] 
SpatialReferenceEnvironment spfactory2 = new SpatialReferenceEnvironment();
ProjectedCoordinateSystem projCoordSys = (ProjectedCoordinateSystem)
    spfactory2.createESRISpatialReferenceFromPRJFile(
    "C:/ArcGIS/java/samples/data/linrear_ref/county.prj");

Using ISpatialReferenceFactory to import and export a spatial reference system

The following code example creates a predefined projected coordinate system, defines its coordinate grid and tolerance values, and exports and imports it two different ways. First it exports the coordinate system to a .prj file, then uses the contents of the .prj file to create a second projected coordinate system.
At the end of this process you might expect that both projected coordinate systems will be identical, but they aren't. PRJ files do not store coordinate grid information, so recreating a spatial reference from a PRJ file will lose any coordinate grid and tolerance information that may have been defined.
Complete equality of spatial references (equal coordinate systems and equal coordinate grids) cannot be checked with one method. IClone.IsEqual compares coordinate systems but not coordinate grids. You need to use other methods to do the latter.
[Java] 
static void importExportSR_Example()throws Exception{
    //Instantiate a predefined spatial reference and set its coordinate grid information.     
    SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
    ProjectedCoordinateSystem pcSystem = (ProjectedCoordinateSystem)
        srFactory.createProjectedCoordinateSystem
        (esriSRProjCSType.esriSRProjCS_WGS1984UTM_10N);
    pcSystem.constructFromHorizon();
    pcSystem.setDefaultXYTolerance();
    //Export the PCS to a PRJ file.
    String fileName = 
        "C:/Program Files/ArcGIS/java/samples/data/linrear_ref/county.prj";
    srFactory.exportESRISpatialReferenceToPRJFile(fileName, pcSystem);
    //Rehydrate it as a new spatial reference object.
    ProjectedCoordinateSystem pcSystem1 = (ProjectedCoordinateSystem)
        srFactory.createESRISpatialReferenceFromPRJFile(fileName);
    //See if they're equal.
    System.out.println(pcSystem.isEqual(pcSystem1)); 
        //Should be true, but you haven't checked coordinate grid information.
    System.out.println(pcSystem.isXYPrecisionEqual(pcSystem1)); 
        //Should be false, PRJ files do not persist coordinate grid information.

}
The ISpatialReferenceFactory3 interface has two methods that are useful when working with low and high precision spatial references. ConstructHighPrecisionSpatialReference creates a high precision spatial reference from a low precision spatial reference. Using this method ensures that coordinate values fit into the new, denser grid mesh. Each intersection of the original grid is an intersection of the new grid.
ConstructLowPrecisionSpatialReference creates a low precision spatial reference from an existing high precision one. You can require that the new resolution value be maintained, possibly at the expense of the x.y domain extent.
Constructing a high or low precision spatial reference
See the following code example that show how to construct a high or low precision spatial reference:
[Java] 
SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
GeographicCoordinateSystem gcSystem = (GeographicCoordinateSystem)
    srFactory.createESRISpatialReferenceFromPRJFile(
    "C:/ArcGIS/Coordinate Systems/Geographic Coordinate Systems/World/WGS 1984.prj");
gcSystem.setIsHighPrecision(true); //Flip this to false if low precision.
gcSystem.constructFromHorizon(); //This is the key; construct horizon then.
gcSystem.setDefaultXYResolution(); //Set Default
double[] xMin = new double[1];
double[] xMax = new double[1];
double[] yMin = new double[1];
double[] yMax = new double[1];
gcSystem.getDomain(xMin, xMax, yMin, yMax);
System.out.println("Domain " + xMin[0] + " " + xMax[0] + " " + yMin[0] + " " +
    yMax[0] + " ");

Converting between low and high precision spatial references

The following code example shows one way to convert a pre-ArcGIS 9.1 low precision spatial reference to an ArcGIS 9.2 high precision spatial reference. The original spatial reference is not modified; a copy is made and altered.
In general, you can construct a high precision spatial reference in any way that makes sense for your ArcGIS 9.1 data. The approach shown here is used for compatibility with ArcSDE dual-resolution data layers, which have a constraint on the relationship between the low and high precision scale factors.
[Java] 
FeatureClass fclass = new FeatureClass(featureWksp.openFeatureClass(
    "VTEST.Counties2"));
ISpatialReference spRef91 = fclass.getSpatialReference();
double[] fx = new double[1];
double[] fy = new double[1];
double[] s = new double[1];
spRef91.getFalseOriginAndUnits(fx, fy, s);
System.out.println("low precision coordinate grid definition:");
System.out.println("false x: " + fx[0] + ", false y: " + fy[0] + ", scale factor: " 
    + s[0]);
SpatialReferenceEnvironment spFactory = new SpatialReferenceEnvironment();
ISpatialReference spRef92 = spFactory.constructHighPrecisionSpatialReference(spRef91,
    - 1,  - 1,  - 1);
spRef92.getFalseOriginAndUnits(fx, fy, s);
System.out.println("high precision coordinate grid definition:");
System.out.println("false x: " + fx[0] + ", false y: " + fy[0] + ", scale factor: " 
    + s[0]);

Geographic coordinate system

A geographic coordinate system includes a name, angular unit of measure, datum (which includes a spheroid), and a prime meridian. It is a model of the earth in a 3D coordinate system. Latitude-longitude, or lat/lon, data is in a geographic coordinate system. You can access the majority of the properties and methods through the IGeographicCoordinateSystem interface with a few more properties available in IGeographicCoordinateSystem2. Although most developers will not need to create a custom geographic coordinate system, the IGeographicCoordinateSystemEdit contains the define and defineEx methods.
The following code example shows how to use the define method to create a user-defined geographic coordinate system. The ISpatialReferenceFactory allows you to create the datum, prime meridian, and angular unit component parts. These components can also be created using a similar define method available on their classes.
[Java] 
// Smart pointer variables used. 
IDatumPtr ipDatum;
IPrimeMeridianPtr ipPrimeMeridian;
IUnitPtr ipUnit;
IAngularUnitPtr ipAngularUnit;
// Create the factory and the component parts. 
ISpatialReferenceFactoryPtr ipFactory(CLSID_SpatialReferenceEnvironment);
ipFactory -  > CreateDatum(esriSRDatum_OSGB1936, &ipDatum);
ipFactory -  > CreatePrimeMeridian(esriSRPrimeM_Greenwich, &ipPrimeMeridian);
ipFactory -  > CreateUnit(esriSRUnit_Degree, &ipUnit);
IGeographicCoordinateSystemEditPtr ipGeoCSEdit(CLSID_GeographicCoordinateSystem);
IGeographicCoordinateSystemPtr ipGCS;
// Query interface (QI) for the angular unit from the unit; 
// this is achieved by the SmartPointers.
ipAngularUnit = ipUnit;
// Make the string descriptions. 
CComBSTR name(_T("User Defined Geographic Coordinate System"));
CComBSTR alias(_T("UserDefined"));
CComBSTR abbreviation(_T("User"));
CComBSTR remarks(_T("User Define GCS based on OSGB1936"));
CComBSTR useage(_T("Suitable for the UK"));
// Make the call HRESULT hr; 
hr = ipGeoCSEdit -  > DefineEx(name, alias, abbreviation, remarks, useage, ipDatum,
    ipPrimeMeridian, ipAngularUnit);
// QI for the result.
ipGCS = ipGeoCSEdit;
To access the hundreds of predefined geographic coordinate systems, ISpatialReferenceFactory has the CreateGeographicCoordinateSystem method. The predefined geographic coordinate systems are listed in the esriSRGeoCSType, esriSRGeoCS2Type, and esriSRGeoCS3Type enumerations. The parts of a geographic coordinate system, such as the datum, angular unit, and prime meridian, are objects as well. All support ISpatialReference2 and ISpatialReferenceFactory. Make use of the predefined objects available in the various esriSR* enumerations.
The IGeographicCoordinateSystem2 interface supplies the AngularConversionFactor method, which will return a value that converts the units of measure between two geographic coordinate systems.
The ExtentHint, LeftLongitude, and RightLongitude properties are interrelated. Usually, data in a geographic coordinate system has longitude values between –180 and 180 if the unit of measure is degrees. Some datasets are designed to use a minimum longitude value of 0 or –360. The LeftLongitude property controls whether the data is considered as –360 to 0, –180 to 180, or 0 to 360. You only need to worry about this if you're inverse projecting projected coordinates for storage in a GCS-based feature class that has a nonstandard longitude range. The ArcObjects framework usually deals with this detail for you. The left longitude property is not considered when comparing two GCS for equality.
GetHorizon returns a WKSEnvelope describing the extent of a geographic coordinate system based on its unit of measure and the LeftLongitude. This method can be used to define a standard coordinate grid for the GCS. It is used internally by the ISpatialReferenceResolution.constructFromHorizon method.

Projected coordinate system

A projected coordinate system includes a name, linear unit of measure, geographic coordinate system, map projection, and any parameters required by map projection. Using the term projection for a coordinate system is imprecise. The term projection should be used for the actual mathematical function.
Transverse mercator and lambert conformal conic are map projections. UTM and state plane are projected coordinate systems that are based on particular map projections. Each projected coordinate system must include a geographic coordinate system. Map projection parameters can be linear, angular, or unitless. A unitless parameter includes scale factor and option. Angular parameters are the central meridian, standard parallels and latitude of origin. Linear parameters are false easting and false northing. Use the getDefaultParameters method on the IProjection interface to determine the parameters a particular map projection expects.
The parts of a projected coordinate system, such as the projection, linear unit, and geographic coordinate system, are objects as well. All support ISpatialReference2 and ISpatialReferenceFactory. When defining a custom projected coordinate system, make use of the predefined objects available in the various esriSR* enumerations.
You can access the majority of the properties and methods through the IProjectedCoordinateSystem2 interface, although a few more properties are available in IProjectedCoordinateSystem3 and IProjectedCoordinateSystem4. The IProjectedCoordinateSystemEdit contains the define method, which allows you to define a custom projected coordinate system. To access the hundreds of predefined projected coordinate systems, ISpatialReferenceFactory has the CreateProjectedCoordinateSystem method. The predefined projected coordinate systems are listed in the esriSRProjCSType, esriSRProjCS2Type, esriSRProjCS3Type, and esriSRProjCS4Type enumerations.
The IProjectedCoordinateSystemEdit interface provides you with the define method to create your own PCS object based on parameters such as name, geographic coordinate system, projected unit, projection and, if necessary, projection parameters.
See the following code example:
[Java] 
//Create a factory.
SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
//Create a projection, GCS and unit using the factory.
Projection projection = (Projection)srFactory.createProjection
    (esriSRProjectionType.esriSRProjection_Sinusoidal);
GeographicCoordinateSystem gcSystem = (GeographicCoordinateSystem)
    srFactory.createGeographicCoordinateSystem(esriSRGeoCSType.esriSRGeoCS_WGS1984);
LinearUnit linearUnit = (LinearUnit)srFactory.createUnit
    (esriSRUnitType.esriSRUnit_Meter);

//Get the default parameters from the projection.
IParameter[] params = new IParameter[16];
//Create a projected coordinate system using the Define method.
ProjectedCoordinateSystem pcSystem = new ProjectedCoordinateSystem();
pcSystem.define("Newfoundland", "NF_LAB", "NF", "Most Eastern Province in Canada", 
    "When making maps of Newfoundland", gcSystem, linearUnit, projection, params);
System.out.println(pcSystem.hasXYPrecision());

Parameters

Parameters are required by both projected coordinate systems and geographic transformations. For example, to define a lambert azimuthal equal area projected coordinate system, only the central meridian and latitude of origin parameters are required by the mathematical algorithm that performs the projection.
The IParameter interface has an index and a value. The value is self-explanatory and refers to the internal array that holds the parameters for a projected coordinate system or a geographic transformation. The ISpatialReferenceFactory can be used to create new parameters.
The following code example shows how to use the create parameter method and the esriSR_ParameterType enumeration. The SpatialReferenceFactory provides default values for each type of parameter. The values can easily be changed.
[Java] 
SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
IParameter parameter = srFactory.createParameter
    (esriSRParameterType.esriSRParameter_LatitudeOfOrigin);
System.out.println(parameter.getName());
System.out.println(parameter.getIndex());
System.out.println(parameter.getValue());
parameter.setValue(45);
System.out.println(parameter.getValue());
The following code example shows how to get the parameters from a projected coordinate system. It assumes that the projected coordinate is already defined. These parameters are passed to the client by reference; it is then possible to modify the value of the parameters directly. If this is done, the IsChanged method on the projected coordinate system must be called.
[Java] 
// pPcs is the projected coordinate system object.
ProjectedCoordinateSystem pCS = new ProjectedCoordinateSystem();
// Create an array of IParameters with 16 elements.
IParameter[][] params = new IParameter[1][16];
pCS.getParameters(params);
for (int i = 0; i < 16; i++){
    IParameter param = params[0][i];
    if (param != null){
        System.out.println(param.getName() + " " + param.getIndex() + " " +
            param.getValue());
    }
}
The following code example shows how to change a parameter using the same variables:
[Java] 
// Get the central meridian parameter.
IParameter param = params[0][2];
if (param != null){
    // Set the new value.
    param.setValue(123);
    // Tell the projected coordinate system that it has changed. 
    pCS.changed();
}
The following example uses the getDefaultParameters method on the IProjection interface to retrieve a set of the required parameters for a projection. Next, set some values and create a new projected coordinate system using these parameters, then make a call to IProjectedCoordinateSystem.getParameters to verify that the parameters have been set.
[Java] 
SpatialReferenceEnvironment srFactory1 = new SpatialReferenceEnvironment();
// Create a projection, gcs and unit using the factory
Projection projection = (Projection)srFactory.createProjection
    (esriSRProjectionType.esriSRProjection_Sinusoidal);
GeographicCoordinateSystem gcSystem = (GeographicCoordinateSystem)
    srFactory.createGeographicCoordinateSystem(esriSRGeoCSType.esriSRGeoCS_WGS1984);
LinearUnit linearUnit = (LinearUnit)srFactory.createUnit
    (esriSRUnitType.esriSRUnit_Meter);
// Get the default parameters from the projection.
IParameter[] params1 = projection.getDefaultParameters();
// Iterate through the parameters and print their name and value.
for (int i = 0; i < params1.length; i++){
    IParameter param1 = params1[i];
    if (param1 == null){
        System.out.println(param1.getName() + " " + param1.getIndex() + " " +
            param1.getValue());
    }
}

// Reset one of the parameter values.
params1[2].setValue(45);
//Generate default parameters for the projection to be created.
IParameter params_v[] = new IParameter[16];
//Create a projection (GCS) and unit using the factory.
Projection projection1 = (Projection)srFactory.createProjection
    (esriSRProjectionType.esriSRProjection_Sinusoidal);
GeographicCoordinateSystem gcSystem1 = (GeographicCoordinateSystem)
    srFactory.createGeographicCoordinateSystem(esriSRGeoCSType.esriSRGeoCS_WGS1984);
LinearUnit linearUnit1 = (LinearUnit)srFactory.createUnit
    (esriSRUnitType.esriSRUnit_Meter);

//Create a projected coordinate system using the Define method.
ProjectedCoordinateSystem pcSystem = new ProjectedCoordinateSystem();
pcSystem.define("Newfoundland", "NF_LAB", "NF", "Most Eastern Province in Canada", 
    "When making maps of Newfoundland", gcSystem1, linearUnit1, projection1,
    params_v[0]);
// Get the parameters from your new projected coordinate system and verify
// that the parameter value was changed.
IParameter[][] params2 = new IParameter[1][16];
pcSystem.getParameters(params2);
// Iterate through the parameters and print their name and value.
for (int i = 0; i < 16; i++){
    IParameter param2 = params[0][i];
    if (param != null){
        System.out.println(param2.getName() + " " + param2.getIndex() + " " +
            param2.getValue());
    }
}

Vertical coordinate system

A vertical coordinate system includes a name, linear unit of measure, vertical or geodetic (horizontal) datum, direction, and optionally, a vertical shift. A vertical coordinate system defines the origin of z-coordinate values. A common application is for z-values to represent elevations or depths if z-values increase up (against the direction of gravity) or down (in the direction of gravity). You can access the majority of the properties and methods through the IVerticalCoordinateSystem interface. Although most developers will not need to create a custom vertical coordinate system, the IVerticalCoordinateSystemEdit contains the define method.
The following code example shows how to use the define method to create user-defined vertical coordinate systems. The ISpatialReferenceFactory interface allows you to create the Datum, VerticalDatum, and LinearUnit component parts. These components can also be created using a similar define method available on their classes.
The first part of the following code example creates a gravity-related vertical coordinate system that uses a vertical datum and the second part creates an ellipsoid-based vertical coordinate system:
[Java] 
// Creates a gravity-related vertical coordinate system.   
VerticalCoordinateSystem vcSystem = new VerticalCoordinateSystem();
SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
VerticalDatum verticalDatum = (VerticalDatum)srFactory.createVerticalDatum
    (esriSRVerticalDatumType.esriSRVertDatum_Taranaki);
// Because a VCS can be based upon Datum or VerticalDatum, IHVDatum is used 
// when defining a vertical coordinate system.
LinearUnit unit = (LinearUnit)srFactory.createUnit(esriSRUnitType.esriSRUnit_Meter);
// The direction is set to -1 and the VerticalShift is set to 40.
vcSystem.define("New VCoordinateSystem", "VCoordinateSystem alias", "abbr", 
    "Test for options", "New Zealand", verticalDatum, unit, new Integer(40), new
    Integer( - 1));

// Creates an ellipsoid-based vertical coordinate system.
VerticalCoordinateSystem vcSystem1 = new VerticalCoordinateSystem();
SpatialReferenceEnvironment srFactory1 = new SpatialReferenceEnvironment();
Datum verticalDatum1 = (Datum)srFactory.createDatum
    (esriSRDatumType.esriSRDatum_WGS1984);
// Because a VCS can be based upon Datum or VerticalDatum, IHVDatum is used 
// when defining a vertical coordinate system.
LinearUnit unit1 = (LinearUnit)srFactory.createUnit(esriSRUnitType.esriSRUnit_Foot);
// The direction is set to -1 and the VerticalShift is set to 40.
vcSystem.define("WGS84 vcs", "WGS84 ellipsoid", "w84 3d", "WGS84 ell-based vcs", 
    "everywhere!", verticalDatum1, unit1, new Double(0.4839), new Double( - 1));
To access the predefined vertical coordinate systems and datums, ISpatialReferenceFactory3 has the createVerticalCoordinateSystem and createVerticalDatum methods. The predefined vertical datums and coordinate systems are listed in the esriSRVerticalDatumType and esriSRVerticalCSType enumerations.

Geographic transformations

Moving your data between projected coordinate systems can involve transforming between geographic coordinate systems. Because geographic coordinate systems contain datums that are based on spheroids, a geographic transformation also changes the underlying spheroid. Other frequently used terms for a geographic transformation include datum shift and geodetic transformation.
A geographic transformation is a mathematical operation that takes the coordinates of a point in one geographic coordinate system and returns the coordinates of the same point in another geographic coordinate system. There is also an inverse transformation to allow coordinates to be put back to the first coordinate system from the second. There are many different types of mathematical operations used to achieve this task.
To outline the previous scenario, consider the following:
Thus, if you have two datasets that are projected, they can be on different projected coordinate systems and their respective coordinate systems can be based on different geographic coordinate systems. It may not be enough to change the parameters of the projected coordinate system. You may experience a misalignment between the two datasets even when both are displayed using a common projected coordinate system. The magnitude of the error varies depending on the geographic coordinate systems used and the relative accuracy of the data. A geographic transformation should minimize these inaccuracies.
Older geographic coordinate systems are usually local systems. They are designed for a region or country. As measuring techniques and data became available, new geographic coordinate systems have often been defined for the same area. A geographic transformation converts data between two geographic coordinate systems. A GeoTransformation includes a name, two geographic coordinate systems (from and to), a method or type, and any parameters required for the method. Each method or type is a class. The following are the available transformation types:
The interfaces on these classes allow you to set any parameters needed by the transformation type. The High Accuracy Reference Network (HARN), North American Datum Conversion (NADCON), and National Transformation Version 2 (NTv2) transformations are grid based. They use a file on disk to calculate the data shifts. Use the IGridTransformation interface to access the on disk information.
Use the IGeoTransformation interfaces to set the from and to spatial references. A GeoTransformation is always defined in a particular direction—FROM geographic coordinate system 1 TO geographic coordinate system 2. The projectEx method on IGeometry2 has a direction parameter. Set it to esriTransformForward if you want to apply the GeoTransformation in the order that it is defined. If you want to apply it in the opposite direction, use esriTransformReverse.
To access the hundreds of predefined geographic transformations, ISpatialReferenceFactory has the createGeoTransformation method. The predefined geographic transformations are listed in the esriSRGeoTransformationType, esriSRGeoTransformation2Type, and esriSRGeoTransformation3Type enumerations. The following code example shows how to create a geotransformation using the spatial reference factory and the getSpatialReferences methods.
[Java] 
SpatialReferenceEnvironment srFactory = new SpatialReferenceEnvironment();
IGeoTransformation geoTransformation = (IGeoTransformation)
    srFactory.createGeoTransformation
    (esriSRGeoTransformationType.esriSRGeoTransformation_OSGB1936_To_WGS1984_1);
ISpatialReference[] fromSR = new ISpatialReference[1];
ISpatialReference[] toSR = new ISpatialReference[1];
geoTransformation.getSpatialReferences(fromSR, toSR);
System.out.println(fromSR[0].getName() + toSR[0].getName());
A CompositeGeoTransformation is a multistep geotransformation. Use the ICompositeGeoTransformation interface when you need to define a geographic transformation operation that requires the use of an intermediate geographic coordinate system. For example, no direct path from one geographic coordinate system to another exists, but you can use a third geographic coordinate system to get from one to another. For example, Cameroon uses the Adindan and Minna geographic coordinate systems. While it is not possible to convert between Adindan and Minna, you can convert both to World Geodetic System 1984 (WGS84); therefore, you can go from Adindan to WGS84, and from WGS84 to Minna. The transformation method actually goes from Minna to WGS84; therefore you need to state that you want to go in the reverse direction (WGS84 to Minna). To specify the direction of a transformation, use the esriTransformDirection enumerations (esriTransformForward and esriTransformReverse).
The forward direction through this composite geotransformation takes you from Adindan to Minna. The reverse direction through this geotransformation takes you from Minna to Adindan. This composite geotransformation has the following components (that is, it has two direction, geotransformation pairs):
Going forward through the composite geotransformation is the same as going forward through the first component geotransformation and backward through the second component geotransformation. Going reverse through the composite geotransformation is the same as going forward through the second geotransformation and backward through the first geotransformation.
You need the component directions and component ordering to define what forward and reverse mean at the composite level—the order is important. Once you build the composite transformation, it acts like a regular transformation.