In this topic
- What is a coordinate system?
- Types of coordinate systems
- What is a spatial reference?
- Geographic coordinate systems
- Geographic (datum) transformations
- Projected coordinate systems
- Map projections
- Projection parameters
- Vertical coordinate systems
What is a coordinate system?
Coordinate systems enable geographic datasets to use common locations for integration. A coordinate system is a reference system used to represent the locations of geographic features, imagery, and observations, such as Global Positioning System (GPS) locations, within a common geographic framework. Each coordinate system is defined by the following:- Its measurement framework, which is either geographic - in which spherical coordinates are measured from the earth's center; or planimetric - in which the earth's coordinates are projected onto a two-dimensional (2D) planar surface
- Units of measurement - typically feet or meters for projected coordinate systems (PCSs) or decimal degrees for latitude-longitude
- Definition of the map projection for a PCS
- Other measurement system properties, such as a spheroid of reference, datum, one or more standard parallels, central meridian, and possible shifts in the x- and y-directions
There are several hundred geographic coordinate systems (GCSs) and several thousand PCSs are available for use. In addition, you can define a custom coordinate system.
Types of coordinate systems
The following are two common types of coordinate systems used in a geographic information system (GIS):- Global or spherical coordinate system, such as latitude-longitude (often referred to as GCS).
- PCS, such as universal transverse Mercator (UTM), Albers Equal Area, or Robinson, all of which (along with numerous other map projection models) provide various mechanisms to project maps of the earth's spherical surface onto a 2D Cartesian coordinate plane. A PCS is referred to as a map projection.
Coordinate systems (geographic and projected) provide a framework for defining real-world locations.
What is a spatial reference?
A spatial reference is a series of parameters that define the coordinate system and other spatial properties for each dataset in the geodatabase. It is typical that all datasets for the same area (and in the same geodatabase) use a common spatial reference definition. A spatial reference includes the following:- Coordinate system
- Coordinate precision with which coordinates are stored (often referred to as the coordinate resolution)
- Processing tolerances, such as the cluster tolerance
- Spatial extent covered by the dataset (often referred to as the spatial domain)
Geographic coordinate systems
A GCS uses a three-dimensional (3D) spherical surface to define locations on the earth. A GCS is often incorrectly called a datum, but a datum is only one part of a GCS. A GCS includes an angular unit of measure, prime meridian, and a datum (based on a spheroid). The spheroid defines the size and shape of the earth model, while the datum connects the spheroid to the earth's surface.
A point is referenced by its longitude and latitude values. Longitude and latitude are angles measured from the earth's center to a point on the earth's surface. The angles are often measured in degrees (or in grads). The following illustration shows the world as a globe with longitude and latitude values:
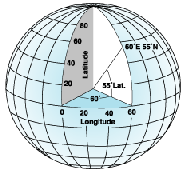

In the spherical system, horizontal lines or east - west lines, are lines of equal latitude or parallels. Vertical lines or north - south lines, are lines of equal longitude or meridians. These lines encompass the globe and form a gridded network called a graticule.
The line of latitude midway between the poles is called the equator. It defines the line of zero latitude. The line of zero longitude is called the prime meridian. For most GCSs, the prime meridian is the longitude that passes through Greenwich, England. The origin of the graticule (0,0) is defined by where the equator and prime meridian intersect.
Latitude and longitude values are traditionally measured in decimal degrees or in degrees, minutes, and seconds (DMS). Latitude values are measured relative to the equator and range from - 90° at the south pole to +90° at the north pole. Longitude values are measured relative to the prime meridian and range from - 180° when traveling west to 180° when traveling east. If the prime meridian is at Greenwich, then Australia, which is south of the equator and east of Greenwich, has positive longitude values and negative latitude values.
It can be helpful to equate longitude values with x and latitude values with y. Data defined on a GCS displays as if a degree is a linear unit of measure. This method is basically the same as the Plate Carrée projection. A physical location usually has different coordinate values in different GCSs.
Geographic (datum) transformations
If two datasets are not referenced to the same GCS, you might need to perform a geographic (datum) transformation. This is a well-defined mathematical method to convert coordinates between two GCSs. As with coordinate systems, there are several hundred predefined geographic transformations that you can access. It is very important to correctly use a geographic transformation if it is required. When neglected, coordinates can be in the wrong location by up to a few hundred meters. Sometimes, no transformation exists or you have to use a third GCS, such as the World Geodetic System 1984 (WGS84) and combine two transformations.
Projected coordinate systems
A PCS is defined on a flat, 2D surface. Unlike a GCS, a PCS has constant lengths, angles, and areas across the two dimensions. A PCS is always based on a GCS that is based on a sphere or spheroid. In addition to the GCS, a PCS includes a map projection, set of projection parameters that customize the map projection for a particular location, and a linear unit of measure.
Map projections
Whether you treat the earth as a sphere or a spheroid, you must transform its 3D surface to create a flat map sheet. This mathematical transformation is commonly referred to as a map projection. One easy way to understand how map projections alter spatial properties is to visualize shining a light through the earth onto a surface, called the projection surface. Imagine the earth's surface is clear with the graticule drawn on it. Wrap a piece of paper around the earth. A light at the center of the earth casts the shadows of the graticule onto the piece of paper. You can now unwrap the paper and lay it flat. The shape of the graticule on the flat paper is different from that on the earth. The map projection has distorted the graticule.
A spheroid cannot be flattened to a plane any more easily than a piece of orange peel can be flattened (it will tear). Representing the earth's surface in two dimensions causes distortion in the shape, area, distance, or direction of the data.
A map projection uses mathematical formulas to relate spherical coordinates on the globe to flat, planar coordinates.
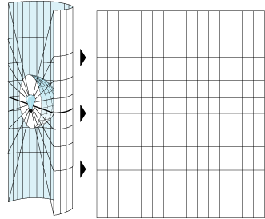
Different projections cause different types of distortions. Some projections minimize the distortion of one or two of the data's characteristics. A projection can maintain the area of a feature, but alter its shape. In the following illustration, data near the poles is stretched:
A spheroid cannot be flattened to a plane any more easily than a piece of orange peel can be flattened (it will tear). Representing the earth's surface in two dimensions causes distortion in the shape, area, distance, or direction of the data.
A map projection uses mathematical formulas to relate spherical coordinates on the globe to flat, planar coordinates.
Different projections cause different types of distortions. Some projections minimize the distortion of one or two of the data's characteristics. A projection can maintain the area of a feature, but alter its shape. In the following illustration, data near the poles is stretched:
Projection parameters
Alone, a map projection is not enough to define a PCS. You can state that a dataset is in Transverse Mercator, but that is not enough information. Where is the center of the projection? Was a scale factor used? Without knowing the exact values for the projection parameters, the dataset cannot be reprojected.
You can also get an idea of the amount of distortion the projection has added to the data. If you are interested in Australia but you know that a dataset's projection is centered at 0,0, the intersection of the equator and the Greenwich prime meridian, you might want to think about changing the center of the projection.
Each map projection has a set of parameters that you must define. The parameters specify the origin and customize a projection for your area of interest. Angular parameters use the GCS units, while linear parameters use the PCS units.
Each map projection has a set of parameters that you must define. The parameters specify the origin and customize a projection for your area of interest. Angular parameters use the GCS units, while linear parameters use the PCS units.
Linear parameters
Angular parameters
- Azimuth defines the centerline of a projection. The rotation angle measures east from north. It is used with the azimuth cases of the Hotine Oblique Mercator projection.
- Central meridian defines the origin of the x-coordinates.
- Longitude of origin defines the origin of the x-coordinates. The central meridian and longitude of origin parameters are synonymous.
- Central parallel defines the origin of the y-coordinates.
- Latitude of origin defines the origin of the y-coordinates. This parameter might not be located at the center of the projection. In particular, conic projections use this parameter to set the origin of the y-coordinates below the area of interest. In that instance, you do not need to set a false northing parameter to ensure that all y- coordinates are positive.
- Longitude of center is used with the Hotine Oblique Mercator center (two-point and azimuth) cases to define the origin of the x-coordinates. It is usually synonymous with the longitude of origin and central meridian parameters.
- Latitude of center is used with the Hotine Oblique Mercator center (both two-point and azimuth) cases to define the origin of the y-coordinates. It is almost always the center of the projection.
- Standard parallel 1 and standard parallel 2 are used with conic projections to define the latitude lines where the scale is 1.0. When defining a Lambert Conformal Conic projection with one standard parallel, the first standard parallel defines the origin of the y-coordinates.
For other conic cases, the y-coordinate origin is defined by the latitude of origin parameter as follows:
- Longitude of first point
- Latitude of first point
- Longitude of second point
- Latitude of second point
The preceding four parameters are used with the Two-Point Equidistant and Hotine Oblique Mercator projections. They specify two geographic points that define the center axis of a projection.
- Pseudo standard parallel 1 is used in the Krovak projection to define the oblique cone's standard parallel.
- X,y plane rotation defines the orientation of the Krovak projection along with the x- and y-scale parameters.
Unitless parameters
- Scale factor is a unitless value applied to the center point or centerline of a map projection. The scale factor is usually slightly less than one. The UTM coordinate system, which uses the Transverse Mercator projection, has a scale factor of 0.9996. Rather than 1.0, the scale along the central meridian of the projection is 0.9996. This creates two almost parallel lines approximately 180 kilometers or about 1° away where the scale is 1.0. The scale factor reduces the overall distortion of the projection in the area of interest.
- X and y scales are used in the Krovak projection to orient the axes.
- Option is used in the Cube and Fuller projections. In the Cube projection, option defines the location of the polar facets. An option of 0 in the Fuller projection displays all 20 facets. Specifying an option value between 1 and 20 displays a single facet.
Vertical coordinate systems
A vertical coordinate system defines the origin for height or depth values. Like a horizontal coordinate system, most of the information in a vertical coordinate system is not needed unless you want to display or combine a dataset with other data that uses a different vertical coordinate system.
Perhaps the most important part of a vertical coordinate system is its unit of measure. The unit of measure is always linear (for example, international feet or meters). Another important part is whether the z-values represent heights (elevations) or depths. For each type, the z-axis direction is positive "up" or "down," respectively.
Perhaps the most important part of a vertical coordinate system is its unit of measure. The unit of measure is always linear (for example, international feet or meters). Another important part is whether the z-values represent heights (elevations) or depths. For each type, the z-axis direction is positive "up" or "down," respectively.
In the following illustration, there are two vertical coordinate systems: mean sea level and mean low water. Mean sea level is used as the zero level for height values. Mean low water is a depth-based vertical coordinate system.
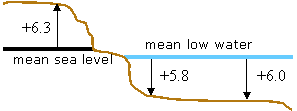
One z-value is shown for the height-based mean sea level system. Any point that falls below the mean sea level line but is referenced to it will have a negative z-value. The mean low water system has two z-values associated with it. Because the mean low water system is depth based, the z-values are positive. Any point that falls above the mean low water line but is referenced to it will have a negative z-value.
You cannot define a vertical coordinate system on a dataset without a corresponding geographic or projected coordinate system.
See Also:
What are geographic coordinate systemsWhat are projected coordinate systems
About map projections
What are vertical coordinate systems
