This document is archived and information here might be outdated.  Recommended version.


Working with vertical polyline segments (ArcObjects .NET 10.8 SDK)
ArcObjects Help for .NET developers > ArcObjects Help for .NET developers > Developing with ArcGIS > Learning ArcObjects > Managing data > Working with geometry > Creating geometries > Working with vertical polyline segments

Working with vertical polyline segments


Summary
At ArcGIS 10, three-dimensional (3D) polylines can contain vertical line segments. They can be stored in geodatabases and used in topologies and network datasets. They can be edited in ArcMap and ArcScene. Two-dimensional (2D) relational operators have been extended to deal reasonably with such polylines. Some geoprocessing tools, such as Clip and Select, preserve vertical segments in their outputs. Vertical segments are not supported in earlier versions of ArcGIS software or geodatabases.

In this topic

Definitions

A 3D polyline is a sequence of paths. Each path is a sequence of vertices connected with straight line segments.
The ArcGIS geometry object model supports parametric curve segments, such as circular arcs and Bezier curves, but the behavior of these segments is not defined in 3D. However, you can use them in 3D polylines if you simply want to use their Z values as attributes and otherwise treat the segment as 2D.
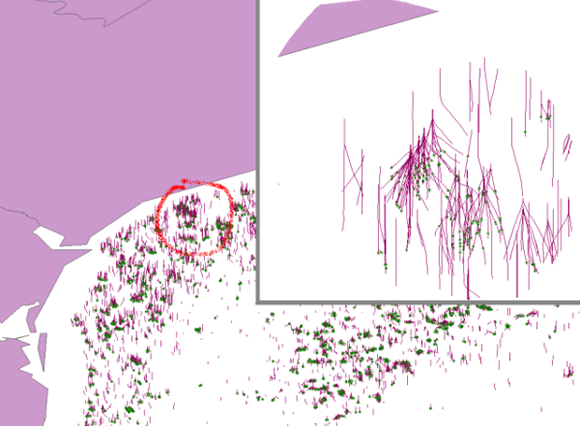
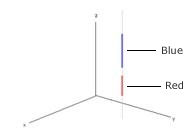
Each vertex is defined with an (x, y, z) coordinate triple. Starting with ArcGIS 10, the (x,y) portions of a pair of successive vertices can be identical. Such a pair is called a vertical line segment. Vertical segments were not permitted in earlier versions of ArcGIS. The following illustration shows an example of oil well data using 3D polylines with vertical segments:
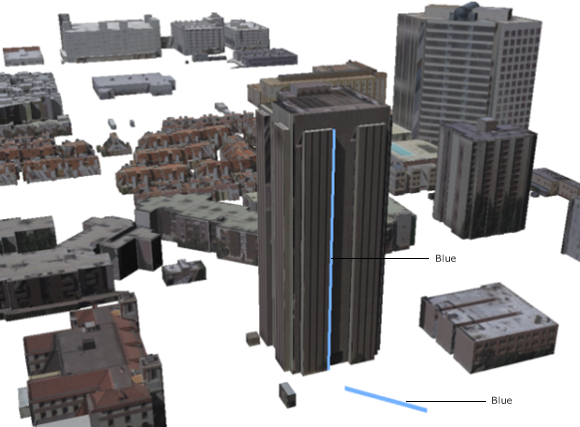
The following illustration shows an example of a multipart 3D polyline in front of a building. One part (path) contains one vertical segment. Such a path is referred to as "purely" vertical.
Vertical polylines can be created and modified by the ArcMap and ArcScene editors. They are supported in ArcGIS 10 geodatabases (including ArcGIS 10 geodatabase topologies) and network datasets. There is limited support for rendering 3D polylines in ArcMap. Cartographic symbols with round edges, for example, can be used. Simple line symbols will not render any purely vertical parts.
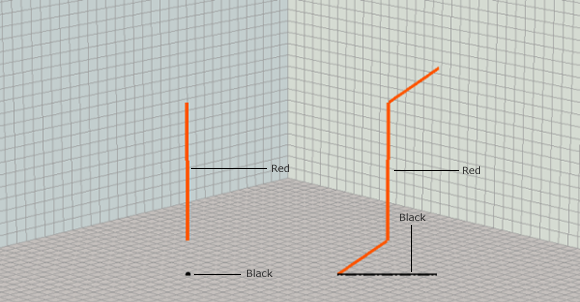
When 2D relational operators are applied to 3D polylines, the 3D polylines are internally converted into 2D hybrid polylines. A hybrid polyline is a collection of 2D paths and 2D points. The 2D hybrid version of the blue 3D polyline in the previous illustration contains one horizontal segment and one point. A second example is shown in the following illustration. The 3D polyline (in red) has two parts: a purely vertical path (on the left), and another path containing an embedded vertical segment. The 2D hybrid version of this polyline (in black) also has two parts - a point and a path with two horizontal segments. The embedded vertical segment is stripped out.

3D polylines and 2D relational operators

3D polylines can be used with 2D relational operators. This section briefly reviews the core ArcGIS 2D relational operators and describes how those operators are extended for 3D polylines. See the IRelationalOperator interface and its corresponding methods for a more detailed overview of relational operators.
The operators are always applied to two input geometries, referred to here as the base and comparison inputs. Each operator is defined in terms of intersections between the boundaries and interiors of the inputs. A point has only an interior (the discussion of points in this section also refers to multipoints). The boundary of a polyline is the set of from and to points of each of its paths.
ArcGIS does not planarize polylines before using them in relational operators. Paths can self intersect, and a closed path still has a from and to point in its boundary point set.
Everything else in a polyline is its interior. The boundary of a polygon is its set of rings viewed as 1D closed paths. The enclosed area is its interior.
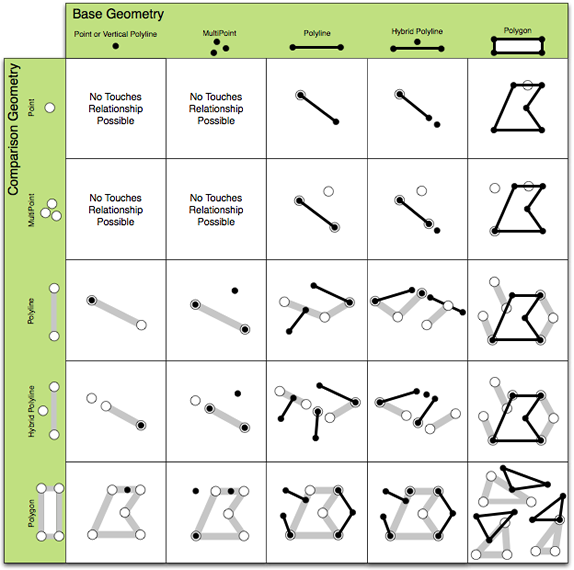
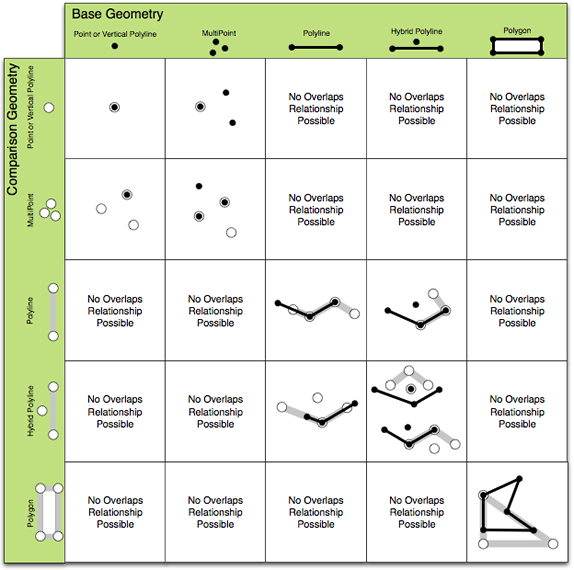
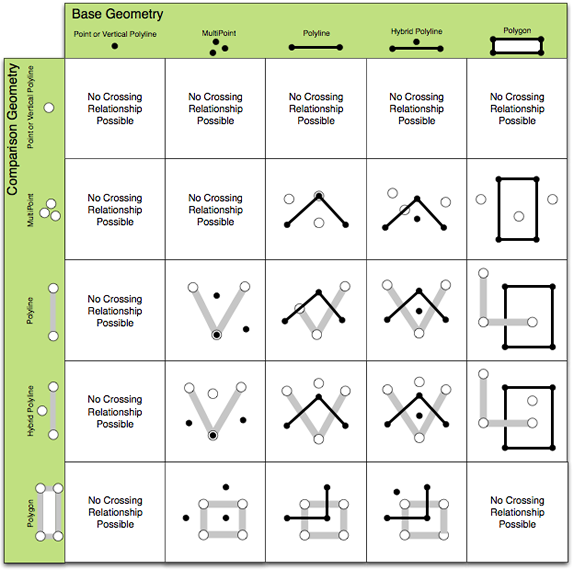
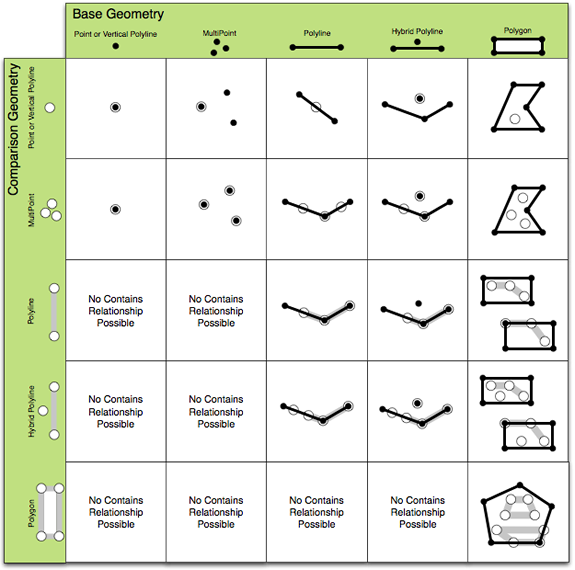
The five core relational operators are described as follows along with illustrations giving an overview of "true" relationships between varying geometry types:
  • Disjoint - Defined for all combinations of geometry types. The boundary and interior of the first input must not intersect the boundary or interior of the second input. See the following illustration:
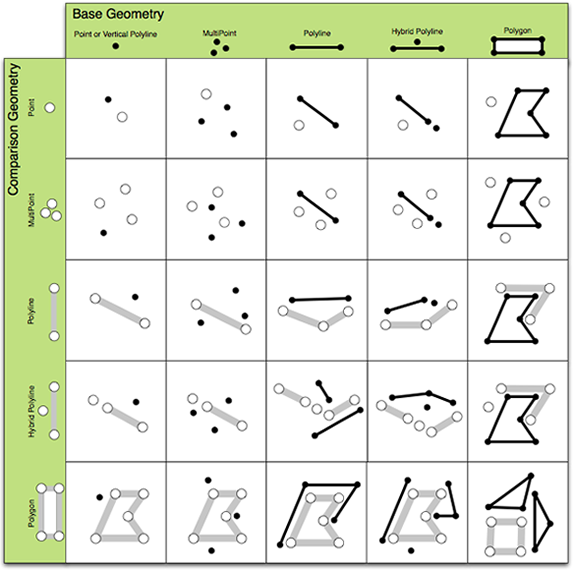
  • Touches - Defined for all geometry types except point-point. Two geometries touch if they intersect but do not share any interior points. See the following illustration:

  • Overlaps - Defined for geometries that have the same dimension (point-point, polyline-polyline, polygon-polygon). Two geometries overlap if their interior intersection is the same dimension as the input dimensions. See the following illustration:

  • Crosses - Defined for line-line and for types with different dimensions (point-line, line-area, and so on). Cross is defined as an interior intersection that has a lower dimension than the max dimension of the inputs. See the following illustration:

  • In (Contains and Within) - Defined for all geometry types. Geometry A is in another geometry B if their intersection equals A and there is an interior intersection. According to this definition, a polyline that is strictly on the boundary of a polygon is not considered to be in the polygon. See the following illustrations (Contains is first):



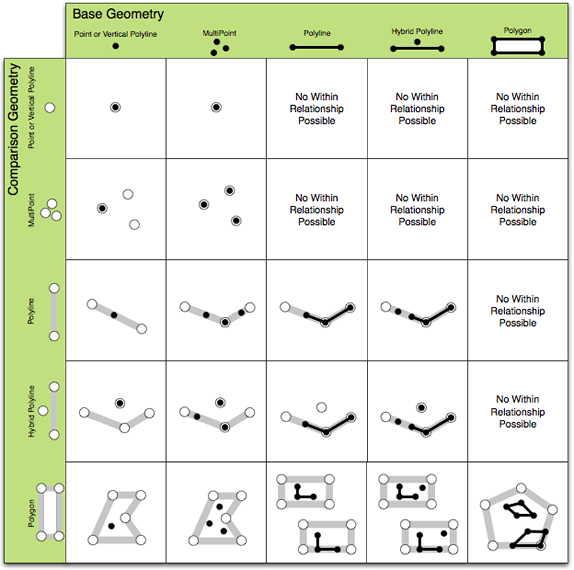
These relationships are mutually exclusive for planar, 2D input geometries.
Relational operators have been extended to support 3D polylines, and that process is generalized in the following steps:
  1. The polyline is converted to a 2D hybrid polyline.
  2. Each of the base inputs is related to parts of the comparison input.
  3. The resulting relations are collected, and a rule is applied to determine the overall result relation.
The following tables define the relations for each type of input involving 2D hybrid representations of 3D polylines. The first column of each table lists the name of the result relation. The second column defines which sub-relationships are used to evaluate each part-part combination. The third column describes how the sub-relationships are combined to produce a true-or-false answer for the result relation.
The first table defines the relations for points and 3D polylines, the second table defines the relations for polylines and other polylines (one or both of which can be 3D), and the third table defines the relations for 3D polylines and polygons.
The following table defines relations between points and 2D hybrid representations of 3D polylines:
Relation name
Sub-relationship names
Combination rule
Touch
Point-point: Not defined
Point-path: Touch
True if a point touches a path.
In
Point-point: In
Point-path: In
True if all parts are in.
Cross
Point-point: In
Point-path: In
True if some but not all parts are in.
Disjoint
Point-point: Disjoint
Point-path: Disjoint
True if all base parts are disjoint from all comparison parts.
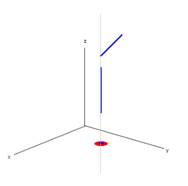
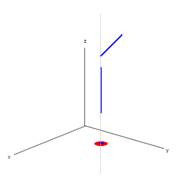
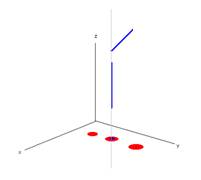
As shown in the examples for point-polyline relationships in the following illustration, these relationships are not mutually exclusive because the set of hybrid 2D points and hybrid 2D paths that represent a 3D polyline can intersect. ArcGIS does not detect and remove intersecting 2D hybrid points before evaluating these relationships.
 
 
 
The point touches the polyline because it touches the xy projection of the upper horizontal path.
The point is also contained in the polyline because it is contained in the 2D point projection of the vertical part.
The points cross the polyline because some but not all of the points are in the polyline. The middle point is in the polyline because it is in the 2D point projection of the vertical polyline part.
The following table defines relations between 2D hybrid representations of pairs of 3D polylines:
Relation name
Sub-relationship names
Combination rule
Touch
Point-point: Not defined
Point-path: Touch
Path-point: Touch
Path-path: Touch
True if any part touches another part.
In
Point-point: In
Point-path: In
Path-point: Not defined
Path-path: In
True if all parts are in.
Cross
Point-point: Not defined
Point-path: In
Path-point: In
Path-path: Cross
True if there is a path-path cross or if some, but not all, parts are in.
Overlap
Point-point: In
Point-path: Not defined
Path-point: Not defined
Path-path: Overlap or In
True if path-path overlap or if some, but not all, parts are in.
Disjoint
Point-point: Disjoint
Point-path: Disjoint
Path-point: Disjoint
Path-path: Disjoint
True if all base parts are disjoint from all comparison parts.
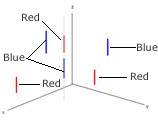
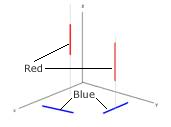
The following illustration shows a sample of the relations described in the previous table:
 
 
 
The red line is in the blue line (and vice versa).
The multipart blue line overlaps the multipart red line because two of the parts project to the same 2D point.
The red and blue lines cross because only one of the red parts projects to a 2D point in the interior of a blue part.
The following table defines relations between 2D hybrid representations of pairs of 3D polygons:
Relation name
Sub-relationship names
Combination rule
Touch
Point-polygon: Touch
Path-polygon: Touch
True if any part touches.
In
Point-polygon: In
Path-polygon: In
True if all parts are in.
Cross
Point-polygon: In
Path-polygon: Cross or In
True if paths cross polygon or if some, but not all, parts are in.
Disjoint
Point-polygon: Disjoint
Path-polygon: Disjoint
True if all base parts are disjoint from all comparison parts.
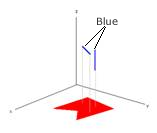
The following illustration shows a sample of the relations described in the previous table:
 
 
 
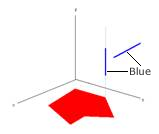
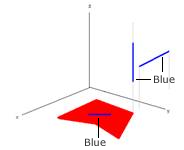
The multipart blue 3D polyline is in the polygon because the 2D hybrid polyline is in the polygon.
The blue 3D polyline touches the polygon because 3D point projection of the vertical part touches it and the blue non-vertical part is outside.
The blue 3D polyline crosses the polygon because the dimension of the intersection of the interiors is less than the maximum dimension of the inputs, and the polyline isn't contained in the polygon.

3D polylines and geoprocessing tools

Vertical line segments are preserved in the outputs of some geoprocessing tools and will be stripped from the outputs of some other tools. The distinction between these kinds of tools is whether they are planar or non-planar. Planar outputs have all self intersections and overlaps removed. Non-planar outputs permit such instances, although intersections and overlaps will have extra vertices placed where such instances occur. Intersect and Union, in the Overlay toolset, are examples of planar geoprocessing tools. Clip and Erase are examples of non-planar geoprocessing tools.

ArcGIS 10 compatibility with earlier geodatabase versions

Prior to ArcGIS 10, vertical line segments were stripped out of polylines. In all versions of the software, including ArcGIS 10, vertical segments are removed from polygons. When ArccGIS 10 is used to edit earlier versions of a geodatabase, vertical line segments cannot be used. Attempts to export or copy and paste feature classes from ArcGIS 10 geodatabases to earlier geodatabase versions will also fail if vertical segments are encountered.





To use the code in this topic, reference the following assemblies in your Visual Studio project. In the code files, you will need using (C#) or Imports (VB .NET) directives for the corresponding namespaces (given in parenthesis below if different from the assembly name):
Development licensing Deployment licensing
ArcGIS Desktop Basic
ArcGIS Desktop Standard
ArcGIS Desktop Advanced
Engine Developer Kit