Disponible con una licencia de Spatial Analyst.
La herramienta Spline utiliza un método de interpolación que estima valores usando una función matemática que minimiza la curvatura general de la superficie, lo que resulta en una superficie suave que pasa exactamente por los puntos de entrada.
Fondo conceptual
Conceptualmente, los puntos de muestra extruden hasta la altura de su magnitud. Spline curva una hoja de goma que pasa a través de los puntos de entrada y minimiza a la vez la curvatura total de la superficie. Ajusta una función matemática a una cantidad especificada de puntos de entrada más cercanos mientras pasa a través de los puntos de muestra. Este método es mejor para generar superficies que varían levemente, como la elevación, la altura de las tablas de agua o las concentraciones de contaminación.
La forma básica de la curvatura mínima de interpolación por Spline impone las siguientes dos condiciones en el interpolante:
- La superficie debe pasar exactamente por los puntos de datos.
- La superficie debe tener una curvatura mínima. La suma acumulativa de los cuadrados de los términos de la derivada segunda de la superficie tomada sobre cada punto de la superficie debe ser un mínimo.
La técnica de curvatura mínima básica también se conoce como interpolación por lámina delgada. Asegura una superficie suave (continua y diferenciable), junto con superficies continuas de derivada primera. En las inmediaciones de los puntos de datos pueden ocurrir cambios rápidos en la gradiente o pendiente (derivada primera), por lo que este modelo no es adecuado para estimar la derivada segunda (curvatura).
La técnica de interpolación básica se puede aplicar utilizando un valor de cero para el argumento de Peso en la herramienta Spline.
Tipos de spline
Hay dos tipos de Spline: Regularizado y de Tensión. El tipo Regularizado crea una superficie suave que cambia gradualmente con valores que pueden estar fuera del rango de datos de muestra. El tipo Tensión controla la rigidez de la superficie en función del carácter del fenómeno modelado. Crea una superficie menos suave con valores que están más restringidos por el rango de datos de la muestra.
Tipo de spline regularizado
La opción REGULARIZED modifica el criterio de minimización para que los términos de la derivada tercera se incorporen a los criterios de minimización. El parámetro de Peso especifica el peso adjunto a los términos de la derivada tercera durante la minimización, que se denomina τ (tau) en la documentación. Los valores más altos de este término producen superficies más suaves. Los valores entre 0 y 0,5 son adecuados. Al utilizar esta opción se garantiza una superficie suave junto con superficies suaves de derivada primera. Esta técnica es útil si es necesario calcular la derivada segunda de la superficie interpolada.
Tipo de spline de tensión
La opción TENSION modifica el criterio de minimización para que los términos de la derivada primera se incorporen a los criterios de minimización. El parámetro de Peso especifica el peso adjunto a los términos de la derivada primera durante la minimización, que se denomina Φ (phi) en la documentación. Un peso de cero resulta en la interpolación por Spline por lámina delgada básica. Al utilizar un valor de peso mayor, se reduce la rigidez de la lámina y, a medida que phi se acerca a infinito en el límite, la superficie se aproxima a la forma de una membrana u hoja de goma que pasa por los puntos. La superficie interpolada es suave. Las derivadas primeras son continuas pero no suaves.
Parámetros adicionales de spline
Es posible lograr un mayor control de la superficie de salida mediante dos parámetros adicionales: el peso y el número de puntos.
Parámetro de peso
Para el método de Spline Regularizado, el parámetro de Peso define el peso de las derivadas terceras de la superficie en la expresión de la minimización de la curvatura. Cuanto más alto es el peso, más suave es la superficie de salida. Los valores introducidos para este parámetro deben ser iguales o mayores que cero. Los valores comunes que pueden usarse son 0; 0,001; 0,01; 0,1 y 0,5.
Para el método de Spline de Tensión, el parámetro de Peso define el peso de la tensión. Cuanto más alto es el peso, más gruesa es la superficie de salida. Los valores introducidos deben ser iguales o mayores que cero. Los valores comunes son 0, 1, 5 y 10.
Parámetro de cantidad de puntos
La Cantidad de puntos identifica el número de puntos que se utilizan en el cálculo de cada celda interpolada. Cuantos más puntos de entrada especifique, mayor será la influencia de los puntos distantes sobre cada celda y más suave será la superficie de salida. Cuanto más grande sea el número de puntos, más tiempo llevará procesar el ráster de salida.
La ecuación de spline
El algoritmo que utiliza la herramienta Spline se basa en la siguiente fórmula para la interpolación de la superficie:
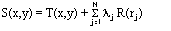
- donde:
j = 1, 2, ..., N.
N es la cantidad de puntos.
λj son coeficientes determinados por la solución de un sistema de ecuaciones lineales.
rj es la distancia del punto (x,y) al punto j.
T(x,y) y R(r) se definen de forma diferente, según la opción seleccionada.
Por cuestiones de cómputo, todo el espacio del ráster de salida está dividido en bloques o regiones de igual tamaño. El número de regiones en las direcciones x e y es el mismo, y tienen forma rectangular. La cantidad de regiones se determina dividiendo la cantidad total de puntos del dataset de puntos de entrada por el valor especificado para la cantidad de puntos. Para los datos distribuidos con menor uniformidad, las regiones pueden contener una cantidad de puntos significativamente diferente, siendo el valor para la cantidad de puntos un mero promedio aproximado. Si en alguna región la cantidad de puntos es menor que ocho, esa región se expande hasta contener un mínimo de ocho puntos.
Para la opción Regularizado
T(x,y) = a1 + a2x + a3y- donde:
ai son coeficientes determinados por la solución de un sistema de ecuaciones lineales.
y
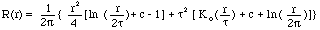
- donde:
r es la distancia entre el punto y la muestra.
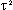es el parámetro de Peso.Ko es la función de Bessel modificada.
c es una constante igual a 0,577215.
Para la opción de Tensión
T(x,y) = a1- donde:
a1 es un coeficiente determinado por la solución de un sistema de ecuaciones lineales.
y
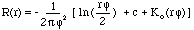
- donde:
r es la distancia entre el punto y la muestra.
φ2 es el parámetro de Peso.
Ko es la función de Bessel modificada.
c es una constante igual a 0,577215.
Procesamiento regional de la salida
Por cuestiones de cómputo, todo el espacio del ráster de salida está dividido en bloques o regiones de igual tamaño. El número de regiones en las direcciones x e y es el mismo, y tienen forma rectangular. La cantidad de regiones se determina dividiendo la cantidad total de puntos del dataset de puntos de entrada por el valor especificado para la cantidad de puntos. Para los datos distribuidos con menor uniformidad, las regiones pueden contener una cantidad de puntos significativamente diferente, siendo el valor para la cantidad de puntos un mero promedio aproximado. Si en alguna región el número de puntos es menor que ocho, esa región se expande hasta contener un mínimo de ocho puntos.
Referencias
Franke, R. 1982. Smooth Interpolation of Scattered Data by Local Thin Plate Splines. Computer and Mathematics with Applications. Vol. 8. N.º 4. Pág. 273–281. Gran Bretaña.
Mitas, L. y H. Mitasova. 1988. General Variational Approach to the Interpolation Problem. Computer and Mathematics with Applications. Vol. 16. N.º 12. Pág. 983–992. Gran Bretaña.