Disponible con una licencia de Geostatistical Analyst.
Cómo se generan las realizaciones
Simulaciones de estadísticas geográficas gaussianas crea primero una cuadrícula de valores asignados aleatoriamente obtenidos de una distribución normal estándar (media = 0 y varianza = 1). El modelo de covarianza (del semivariograma especificado en la capa del kriging simple, que se necesita como entrada para la simulación) se aplica a continuación al ráster. Esto garantiza que los valores de ráster se adaptan a la estructura espacial encontrada en el dataset de entrada. El ráster resultante constituye una realización incondicional y se pueden generar muchas más usando cada vez un ráster diferente de valores con una distribución normal. Se pueden leer más detalles sobre este método en Dietrich y Newsam (1993).
Si se ha seleccionado la simulación condicional, los rásteres incondicionales se condicionan por medio del método kriging. Este proceso usa la estimación de kriging (predicción) de cada ubicación para garantizar que los valores simulados respetan los valores de los datos de entrada y que, en promedio, las predicciones de kriging se replican. Los detalles del condicionamiento de las realizaciones con kriging se puede consultar en Journel (1974).
Sin embargo, si el modelo de kriging simple incluye error de medición, los valores de los datos de entrada no se respetarán (en la capa de kriging simple o en las realizaciones simuladas). Además de esto, la herramienta Simulaciones de estadísticas geográficas gaussianas se ha implementado de modo que use una vecindad de búsqueda continua (o suave) que evite las discontinuidades en las superficies simuladas debidas a los cambios en la vecindad local empleada en kriging. Puede encontrar detalles en Aldworth (1998) y en Gribov y Krivoruchko (2004).
Para obtener más información sobre los conceptos de las simulaciones de estadísticas geográficas y ejemplos de simulaciones condicionales y no condicionales, consulte la sección de la Ayuda sobre los conceptos clave de la simulación de estadísticas geográficas.
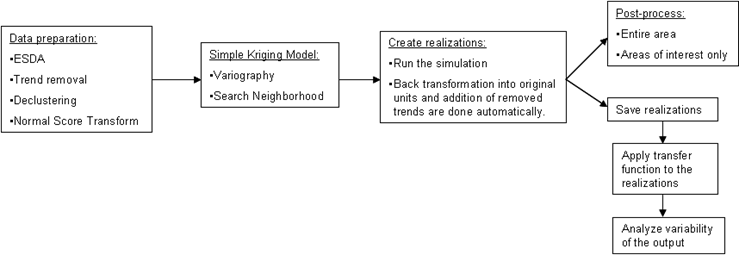
Un flujo de trabajo general de la simulación de estadísticas geográficas gaussianas incluye preparar los datos, crear las realizaciones, volver a transformar los resultados en las unidades originales y posprocesar los resultados o usarlos como entrada de una función de transferencia (modelo) para valorar la variabilidad de la salida del modelo. Este proceso se representa en la siguiente figura:
Modelos de kriging simple para la simulación
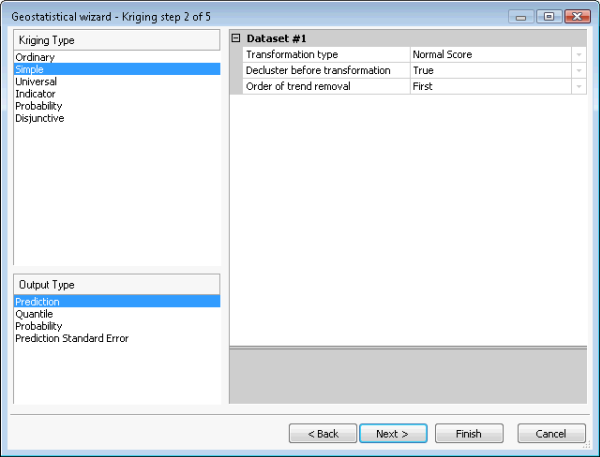
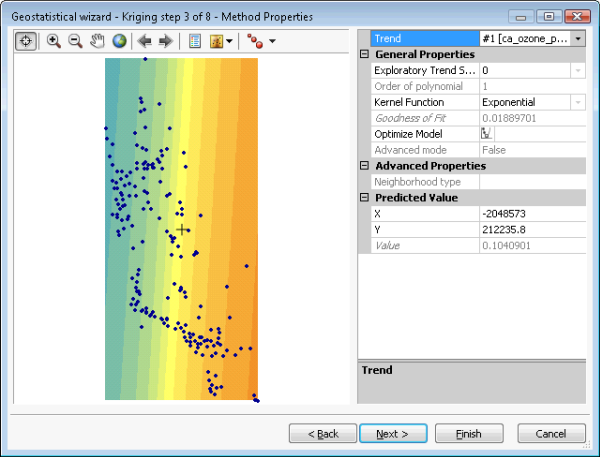
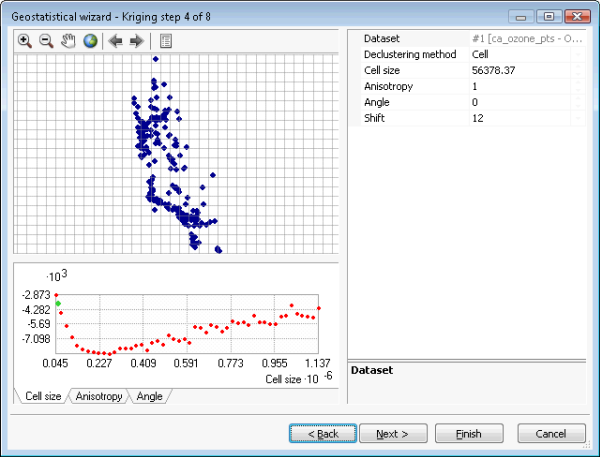
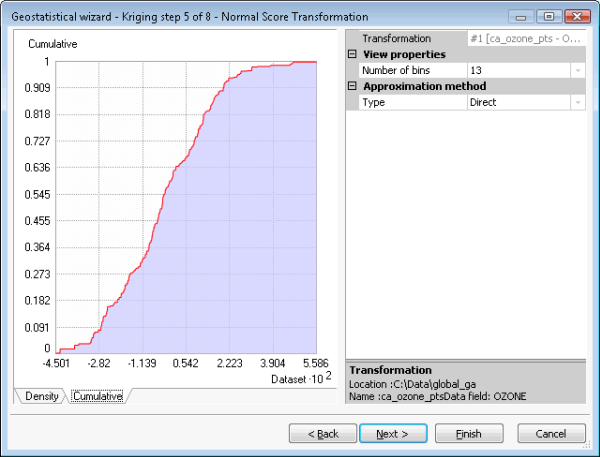
La herramienta Simulaciones de estadísticas geográficas gaussianas acepta cualquier modelo kriging simple. Sin embargo, los resultados de la simulación solo son válidos si los datos de entrada (que se emplean para ajustar el semivariograma y para condicionar las realizaciones) tienen una distribución normal. Esto se puede conseguir aplicando una transformación de puntuación normal. Se debe realizar un declustering para obtener un histograma representativo a partir de los datos agrupados y se deben eliminar las tendencias para garantizar que la media es estacionaria en el dominio espacial. Estos pasos se ilustran en las figuras siguientes. La figura (a) muestra un kriging simple con las opciones de eliminación de tendencia, declustering y transformación de puntuación normal seleccionadas. La figura (b) muestra la tendencia que se eliminará del dataset antes de aplicar el declustering, la transformación de puntuación normal y la variografía. La figura (c) muestra el declustering por celdas. La figura (d) muestra la transformación de puntuación normal, que en este caso usa el método directo.
Comprobar salida de la simulación
Las realizaciones se deben comprobar para confirmar que:
- Los valores de salida, sus patrones espaciales y las ubicaciones son razonables.
- El histograma de los datos simulados reproduce, en promedio, el histograma de los datos de entrada.
- Los semivariogramas de los datos simulados reproducen, en promedio, el semivariograma de los datos de entrada.
- Para la simulación condicional, los valores de entrada se respetan (a menos que el modelo de kriging simple incluya error de medición).
Posprocesamiento
Una vez que se han producido las realizaciones, se posprocesan para obtener resúmenes de los resultados. La herramienta Simulaciones de estadísticas geográficas gaussianas ofrece varias opciones de posprocesamiento que se pueden aplicar en toda la extensión espacial de los rásteres o en áreas de especial interés. Estas áreas se definen mediante la especificación de una clase de entidad poligonal en la opción Polígonos estadísticos de entrada de la herramienta. La salida es similar en los dos casos: al posprocesar todos los rásteres se producen rásteres de resumen, mientras que al posprocesar las áreas poligonales se produce una clase de entidad poligonal de salida que contiene un resumen de estadísticas para cada polígono.
Posprocesar toda la extensión del ráster
- Los rásteres de salida incluyen el valor mínimo generado para cada ubicación (celda), así como el máximo, la media, la desviación estándar, el primer cuartil, la mediana (segundo cuartil) y el tercer cuartil. Además, puede especificar un cuantil que devolverá un valor correspondiente a ese cuantil basado en la distribución de valores simulados en cada celda. También puede especificar un valor de umbral que devolverá el porcentaje de valores simulados que exceden el umbral para cada celda.
- La extensión que se va a posprocesar se puede limitar especificando un polígono de delimitación o un conjunto de puntos (en este caso, se genera una envoltura convexa que se usa como polígono de delimitación). Los valores solo se simulan dentro del polígono de delimitación.
Posprocesar para áreas de interés
- Cuando se especifican áreas de interés poligonales, la salida de cada polígono incluye automáticamente las estadísticas resumidas que se describen en la tabla siguiente. Además, puede especificar un valor cuantil y un valor de umbral (como cuando se posprocesa toda la extensión del ráster). La salida que se genera cuando se seleccionan estas opciones también se describe en la tabla.
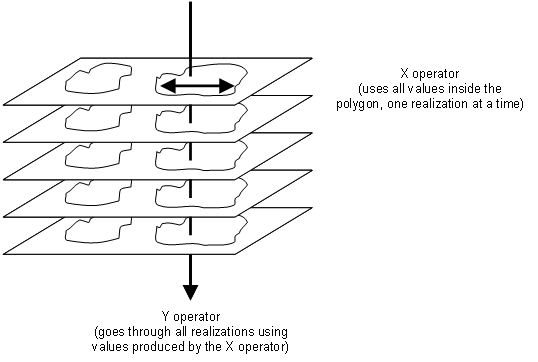
- La salida resumida para los polígonos se calcula usando operadores como los representados en la figura siguiente. El operador X utiliza todos los valores contenidos en el polígono y calcula un valor para cada realización. El operador Y usa valores de todas las realizaciones. Las entradas del operador Y son los valores de las áreas poligonales de cada realización, calculados por el operador X.
Los significados de los campos de la clase de entidad de salida se muestran en la siguiente tabla.
| Nombre de campo | Descripción |
|---|---|
MIN | Valor mínimo de cualquier celda en todas las realizaciones contenidas en el polígono. |
MAX | Valor máximo de cualquier celda en todas las realizaciones contenidas en el polígono. |
MEAN | Media de todas las celdas en todas las realizaciones contenidas en el polígono. |
STDDEV | Desviación estándar de todas las celdas en todas las realizaciones contenidas en el polígono. |
QUARTILE1 | Valor del primer cuartil de todas las celdas en todas las realizaciones contenidas en el polígono. |
MEDIAN | Valor de la mediana de todas las celdas en todas las realizaciones contenidas en el polígono. |
QUARTILE3 | Valor del tercer cuartil de todas las celdas en todas las realizaciones contenidas en el polígono. |
CUANTIL | Valor correspondiente a un cuantil especificado por el usuario para todas las celdas en todas las realizaciones contenidas en el polígono. |
P_THRSHLD | Porcentaje de celdas que sobrepasan un valor de umbral especificado por el usuario para todas las celdas de todas las realizaciones contenidas en el polígono. |
X_Y | La función X se aplica a los valores de las celdas contenidas en el polígono, tomando las realizaciones de una en una. Este proceso es equivalente a ejecutar la herramienta Estadísticas zonales usando el polígono como zona y una realización cada vez como cuadrícula de valores. La función Y se aplica a los valores producidos por la función X.
|
CELL_COUNT | Número de celdas contenidas en el polígono. Si el centro de la celda está dentro del polígono, esa celda se considera contenida en el polígono. Un recuento negativo indica que parte del polígono queda fuera de la extensión del ráster simulado o parte del polígono queda fuera del límite de recorte. El número negativo indica el número total de celdas que se encuentran dentro del polígono. |
SOURCE_ID | Id. de entidad u objeto de la clase de entidad poligonal de entrada. |
Para las opciones del polígono de delimitación y las áreas de interés poligonales, las celdas ráster se consideran contenidas en los polígonos si el centro de la celda está dentro del límite del polígono.
Ejemplo de simulación condicional y salida de posprocesamiento
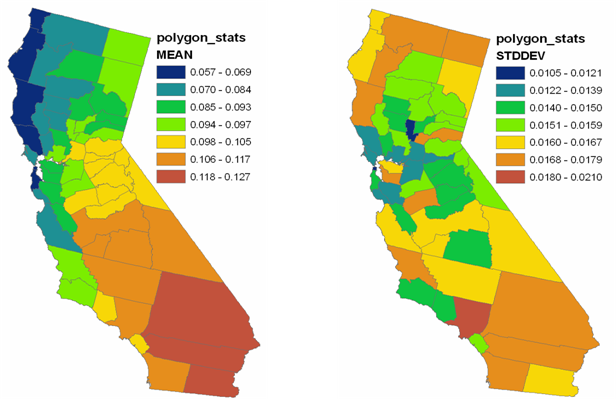
La figura siguiente muestra los resultados de la simulación condicional con el posprocesamiento poligonal de la salida. Los mapas muestran la media y la desviación estándar de cien realizaciones de valores de ozono para los distintos condados de California. Estos valores medios y de desviación estándar se podrían usar, por ejemplo, en estudios epidemiológicos en los que la incidencia de una enfermedad se tiene que comparar con el valor medio del ozono para cada condado.
Referencias y bibliografía adicional
Aldworth, J. 1998. Spatial Prediction, Spatial Sampling, and Measurement Error. Tesis doctoral, Iowa State University. 186.
Chiles, J. P. y P. Delfiner. 1999. Geostatistics: Modeling Spatial Uncertainty. Nueva York: John Wiley & Sons, 449-471.
Deutsch, C. V. y A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide, 2.ª edición. Nueva York: Oxford University Press, 119-141.
Dietrich, C. R. y G. N. Newsam. 1993. "A Fast and Exact Method for Multidimensional Gaussian Stochastic Simulations". Water Resources Research 29 (8): 2861-2869.
Goodchild, M. F., B. O. Parks y L. T. Steyaert. 1993. Environmental Modeling with GIS. Nueva York: Oxford University Press, 432-437.
Gribov, A. y K. Krivoruchko. 2004. "Geostatistical Mapping with Continuous Moving Neighborhood". Mathematical Geology 36 (2): 267-281.
Journel, A. G. 1974. "Geostatistics for Conditional Simulation of Ore Bodies". Economic Geology 69: 673-687.
Leuangthong, O., J. A. McLennan y C. V. Deutsch. 2004. "Minimum Acceptance Criteria for Geostatistical Realizations". Natural Resources Research 13 (3): 131-141.