La Interpolación kernel es una variante de la Interpolación polinómica local de primer orden en la que se evita la inestabilidad en los cálculos gracias a un método similar al utilizado en la regresión de la cresta para calcular los coeficientes de regresión. Cuando la estimación solo tiene un pequeño sesgo y es mucho más precisa que un estimador sin sesgo, bien pudiera tratarse del estimador preferido. Puede consultar más información sobre la regresión de cresta, por ejemplo, en Hoerl y Kennard (1970).
Los errores en la predicción de la Interpolación polinómica local se calculan dando por supuesto que el modelo es correcto; es decir, que el número de la condición espacial es reducido en todos los casos. Normalmente, esta suposición se infringe y el número de condición espacial resalta áreas en las que los errores de predicción y los errores estándar de la predicción son inestables. En el modelo de Suavizado de kernel, el problema con el exceso de errores estándar de la predicción y las predicciones cuestionables se corrigen con el parámetro de cresta, introduciendo una pequeña cantidad de sesgo a las ecuaciones. De este modo, el mapa del número de condición espacial ya no es necesario. Por lo tanto, la Interpolación kernel ofrece solamente errores de predicción y errores estándar de la predicción para el tipo de superficie de salida. Dado que el parámetro de cresta introduce un sesgo con el fin de estabilizar las predicciones, el parámetro de cresta debería ser lo más reducido posible sin dejar de mantener la estabilidad del modelo. Encontrará más detalles sobre este proceso en el documento “Local Polynomials for Data Detrending and Interpolation in the Presence of Barriers”, Gribov y Krivoruchko (2010).
Otra de las diferencias entre los dos modelos es que en el modelo de Interpolación kernel se utiliza la distancia más corta entre dos puntos, de modo que los puntos de los lados de la barrera no transparente (absoluta) especificada se conectan mediante una serie de líneas rectas.
En la interpolación kernel se utilizan los siguientes kernels de simetría radial: Exponential, Gaussian, Quartic, Epanechnikov, Polynomial of Order 5 y Constant. El ancho de banda del kernel viene determinado por un rectángulo alrededor de las observaciones.
Normalmente, con el kernel Epanechnikov se obtienen mejores resultados cuando se utilizan polinómicos de primer orden. Sin embargo, dependiendo de los datos, los diagnósticos de validación y validación cruzada podrían sugerir otro kernel, el de Fan y Gijbels (1996).
A continuación se comparan predicciones de la Interpolación kernel con barreras con barreras absolutas, a la izquierda, sin ellas y a la derecha. Observe cómo las curvas de nivel cambian bruscamente en las barreras del gráfico de la izquierda, mientras que las curvas de nivel fluyen suavemente sobre las barreras del gráfico de la derecha.
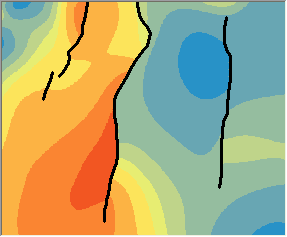
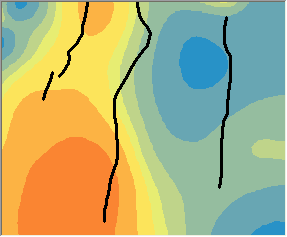
En las aplicaciones hidrológicas y meteorológicas se prefieren modelos basados en la distancia más corta entre puntos.
Funciones kernel
Funciones kernel: para todas las fórmulas de abajo, r es un radio centrado en el punto s y h es el ancho de banda.
- Exponential:
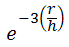
- Gaussian:
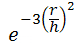
- Quartic:
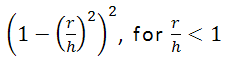
- Epanechnikov:
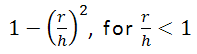
- PolynomialOrder5:
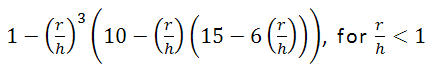
- Constant:
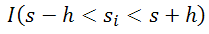
donde I(expresión) es una función de indicador que adopta el valor de 1 si la expresión es verdadera y el valor de 0 si la expresión es falsa.
El parámetro de ancho de banda se aplica a todas las funciones de kernel, salvo Constant. Las funciones de kernel Exponential, Gaussian y Constant admiten también el vecindario de búsqueda uniforme a fin de limitar el rango del kernel.
Referencias y bibliografía adicional
Fan, J. and Gijbels, I. (1996). Local Polynomial Modelling and Its Applications, Chapman & Hall. London.
Hoerl, A.E. and Kennard, R.W. (1970), Ridge regression: biased estimation for nonorthogonal problems, Technometrics, 12, 55-67.
Yan, Xin. (2009) Linear regression analysis : theory and computing. Publicado por World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224.