Disponible con una licencia de Geostatistical Analyst.
El semivariograma representa la autocorrelación espacial de los puntos de muestra medidos. Una vez que se ha trazado cada par de ubicaciones (Agrupar el semivariograma empírico), se ajusta un modelo a través de ellas (Ajustar un modelo al semivariograma empírico). Hay ciertas características que se utilizan normalmente para describir estos modelos.
Rango y meseta
Al observar el modelo de un semivariograma, notará que, a una determinada distancia, el modelo se nivela. La distancia a la que el modelo comienza a aplanarse se denomina rango. Las ubicaciones de muestra separadas por distancias más cortas que el rango están autocorrelacionadas espacialmente, mientras que las ubicaciones que están más alejadas que el rango, no lo están.
El valor en el cual el modelo de semivariograma alcanza el rango (el valor en el eje y) se denomina meseta. Una meseta parcial es la meseta menos el nugget.
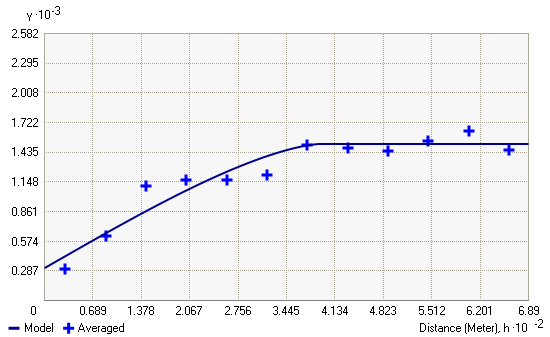
Nugget
En teoría, a una distancia de separación cero (intervalo = 0), el valor del semivariograma es 0. No obstante, a una distancia de separación infinitesimalmente pequeña, el semivariograma a menudo muestra un efecto nugget, que es un valor mayor que 0. Por ejemplo, si el modelo de semivariograma intercepta el eje y en 2, entonces el nugget es 2.
El efecto nugget se puede atribuir a errores de medición o a fuentes espaciales de variación a distancias que son menores que el intervalo de muestreo (o a ambas cosas). Los errores de medición ocurren debido al error inherente a los dispositivos de medición. Los fenómenos naturales pueden variar espacialmente en un rango de escalas. La variación a microescalas más pequeñas que las distancias de muestreo aparecerán como parte del efecto nugget. Antes de recopilar datos, es importante comprender las escalas de variación espacial.