Disponible con una licencia de Spatial Analyst.
El transporte de solutos en un medio poroso implica dos mecanismos principales: advección y dispersión hidrodinámica. La advección describe el transporte pasivo de un soluto con el fluido que se transporta. La dispersión es la mezcla del soluto con el fluido mediante un movimiento diferencial de los fluidos hasta los espacios de los poros. La Dispersión tipo puff asume que el acuífero se mezcla verticalmente; es decir, la concentración es la misma en toda la sección vertical. Esto permite la aplicación de un modelo matemático en dos dimensiones, según lo requiere el modelo de datos ráster.
Dispersión de dos dimensiones
La dispersión de dos dimensiones en un medio poroso está controlada por la ecuación de advección-dispersión (Bear, 1979; Freeze y Cherry, 1979; y Marsily, 1986), escrita en términos de direcciones longitudinales (en la dirección del flujo) y transversales (perpendicular a la dirección del flujo) XL y XT, respectivamente, como:
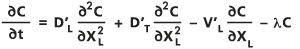
- donde:
C: la concentración del soluto como función de dos dimensiones espaciales y tiempo t.
∂C/∂t: representa el derivado del tiempo.
D'L: los coeficientes de dispersión (retardada) efectiva en la dirección longitudinal.
D'T: los coeficientes de dispersión (retardada) efectiva en la dirección transversal.
λ: el coeficiente de decaimiento, que se supone que es una constante para el decaimiento exponencial de primer orden.
Coeficientes de dispersión
El coeficiente de dispersión es una medición de la extensión en la que se expande el soluto en la dirección especificada:
D'i = Di/R
- donde:
R: El factor de retardo.
i: la dirección (longitudinal o transversal).
el coeficiente de dispersión está relacionado con el comportamiento del soluto en un medio determinado.
Relación entre la dispersión y el coeficiente de dispersión
Las dispersiones αL (dispersión longitudinal) y αT (derivado de la relación de dispersión) están relacionados con los coeficientes de dispersión por:
D'L = αL V' y
D'T = αT V'
donde:
V': la velocidad retardada promedio de la dispersión tipo puff.
XL: el desplazamiento en la dirección longitudinal, paralelo a la dirección del flujo en el centroide de la masa.
XT: el desplazamiento en la dirección transversal, perpendicular a la dirección del flujo en el centroide de la masa.
V'L: la velocidad del soluto retardada en la dirección longitudinal.
En el flujo de agua subterránea:
V = q / n
- donde:
q: el flujo Darcy (descarga por área seccional cruzada).
n: la porosidad efectiva de la formación geológica.
V' = V / R
Consulte la documentación sobre Velocidad Darcy para obtener un análisis más detallado de las velocidades de transporte.
Dispersión gaussiana
La solución aproximada para esta ecuación utilizada en la Dispersión tipo puff está basada en el supuesto de la dispersión gaussiana de un origen de punto instantáneo en un dominio de dos dimensiones con una concentración inicial de cero (por ejemplo, un acuífero limpio mezclado verticalmente), y se calcula con la siguiente ecuación:
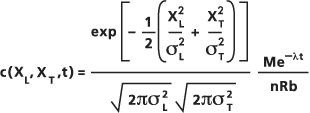
- donde:
M: la masa de soluto liberada instantáneamente en el origen, en unidades de masa.
n: la porosidad del acuífero.
R: El factor de retardo.
b: el grosor del acuífero en unidades de longitud.
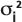: la varianza de la distribución gaussiana en las direcciones longitudinales y transversales, determinada como una función de la dispersión longitudinal y la relación de dispersión proporcionada y la longitud de la ruta del viaje del centro de la masa del soluto que se obtiene en el archivo de recorrido.
A continuación se muestra la forma elíptica general de esta función de distribución gaussiana bivariada:
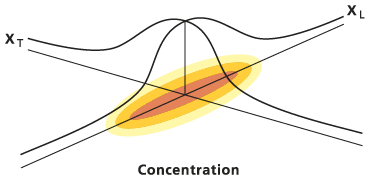
Hay varias limitaciones notables y supuestos implícitos en la solución de la Dispersión tipo puff. La elipse de dispersión se centra en la masa del soluto, que se supone que se ha movido a lo largo del recorrido del flujo descrito en el archivo de entrada. La orientación de la elipse también se fija al recorrido del flujo, con la tangente del eje principal hacia el recorrido del centroide. La porosidad y el grosor, que también contribuyen a la distribución, se interpolan desde sus respectivos rásteres en el centroide, sin incorporar información de las celdas circundantes. Usted debe proporcionar el retardo, el tiempo, el coeficiente de decaimiento, la dispersión longitudinal y la relación de dispersión como constantes.
Dispersión
La dispersión es un parámetro que controla la dispersión de un soluto en un medio poroso y se especifica en unidades de longitud. En el modelo de Dispersión tipo puff, la dispersión se utiliza para calcular la varianza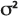 
de la ecuación de dispersión gaussiana que aparece arriba, según:
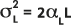y 
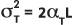
La naturaleza de la dispersión y los métodos para su determinación son temas de gran interés y controversia en la comunidad del modelado de agua subterránea, y no existe una manera mundialmente reconocida de calcular sus valores. En Gelhar et al puede encontrar un análisis de las dispersiones en varias formaciones geológicas. (1992).
El siguiente gráfico resume una variedad de datos de literatura publicada y relaciona la dispersión longitudinal con la escala del problema de interés, es decir, la distancia desde la ubicación de origen hasta el punto de observación.
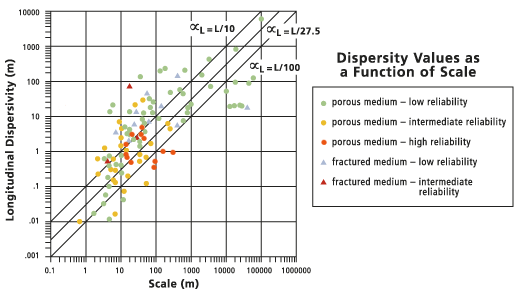
La línea sólida (la línea central) en el gráfico representa el valor predeterminado para la dispersión longitudinal que calcula la herramienta Dispersión tipo puff.
La línea se crea a partir de un ajuste de regresión lineal del
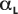hasta L, lo que resulta en 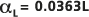una 
o una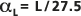 
, en la que la longitud de la ruta del viaje L es la escala de observación.También se muestran las estadísticas de esta regresión. Las líneas exteriores punteadas se colocan en 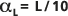la
y la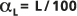 
para compararlas.
Este cálculo predeterminado se debe utilizar como guía solamente, debido a que algunos investigadores no están de acuerdo con el uso de un ajuste tan universal. Para cualquier escala o sitio en particular, las dispersiones válidas pueden tener más de dos órdenes de magnitud, con los cálculos más confiables presentando una tendencia hacia los valores más bajos. En lugar de utilizar el valor predeterminado, que no tiene una base teórica, debe realizar varias simulaciones utilizando un rango de dispersiones. Si se tiene en cuenta a un conjunto de resultados, esto puede ser más válido que utilizar los resultados de una simulación.
Algunas advertencias similares se aplican a la estimación de la relación de dispersiones longitudinales a transversales que se presenta en la siguiente figura. Estos valores generalmente se relacionan con una relación simple, aunque nuevamente, debe experimentar con un rango de valores.
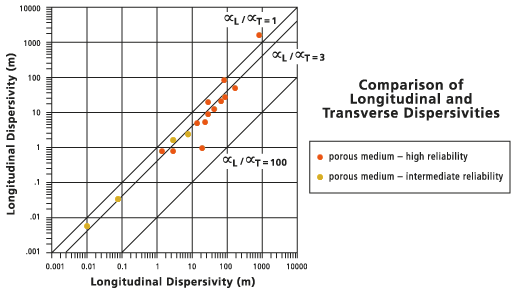
La relación de dispersión predeterminada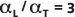 
se indica con la línea sólida (la línea central) en la imagen que aparece a continuación. Las líneas punteadas (las líneas exteriores) se colocan en la 
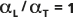y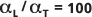 
para compararlas.
Gelhar et al incluye valores para la porosidad y transmitividad efectiva en la tabulación. En Freeze y Cherry (1979) y Marsily (1986) se pueden encontrar tablas para estos valores.
Retardo
El retardo es la relación entre la velocidad del fluido que se transporta y la velocidad del soluto, y se expresa como un número entre uno y el infinito, sin unidades. Un retardo de dos significa que el soluto migra por el medio poroso a la mitad de la velocidad de filtración. Un rastreador ideal no experimenta ninguna adsorción y viaja en la solución con el fluido. Un soluto con esas características tiene un retardo de uno, es decir, se mueve a la misma velocidad que el fluido que se transporta.
Este fenómeno es el resultado de la adsorción y desorción del componente en la matriz porosa, especialmente en las capas orgánicas de las paredes de los poros. La ecuación de retardo se presenta en una discusión de Freeze y Cherry (1979) como:
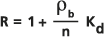
donde:
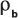: la densidad del volumen de la matriz.n: la porosidad de la formación.
Kd: el coeficiente de distribución, que representa la partición debido a una adsorción rápida y reversible de un soluto entre fases líquidas y sólidas que suponen una isoterma lineal.
Marsily (1986) también analiza el factor de retardo y la adsorción en detalle.
Realizar un modelado de advección-dispersión
Las herramientas Flujo Darcy, Recorrido de una partícula y Dispersión tipo puff se pueden utilizar para realizar un modelado de advección-dispersión rudimentario de los componentes del agua subterránea. Flujo Darcy genera un campo de velocidad de flujo de agua subterránea a partir de datos geológicos, Recorrido de una partícula sigue la ruta de advección a través del campo de flujo desde un origen de punto, y Dispersión tipo puff calcula la dispersión hidrodinámica de la liberación de punto instantánea de un constituyente a medida que es transportado por advección a lo largo de la ruta de flujo.
En Tauxe (1994) se presenta un análisis completo del modelado de advección-dispersión utilizando estas herramientas.
La secuencia típica para el modelado de aguas subterráneas es Flujo Darcy, después Recorrido de una partícula y, a continuación, Dispersión tipo puff.
Ejemplo
- Ejemplo del cuadro de diálogo de la herramienta Dispersión tipo puff:
Archivo de recorrido de una partícula de entrada: ttrack.txt
Ráster de entrada de la formación de porosidad efectiva: poros
Ráster de grosor saturado de entrada: thickn
Ráster de salida: ppuff1
Masa: 3.2e7
Tiempo de dispersión: 50000
Dispersión longitudinal: 6
Relación de dispersión: 3
Factor de retardo: 1
Coeficiente de decaimiento: 250
- Ejemplo del uso de Dispersión tipo puff en álgebra de mapas:
outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
- Secuencia de expresiones de álgebra de mapas que involucra el conjunto de herramientas del modelado de agua subterránea:
out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1) ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp) out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
Referencias
Bear, J. 1979, Hydraulics of Groundwater. McGraw–Hill.
Freeze, R. A. y J. A. Cherry. 1979. Groundwater. Prentice-Hall.
Gelhar, L. W., C. Welty y K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955–1974.
Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.
Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., Universidad de Texas, Austin.