Disponible con una licencia de Geostatistical Analyst.
Voronoi maps are constructed from a series of polygons formed around the location of a sample point.
Voronoi polygons are created so that every location within a polygon is closer to the sample point in that polygon than any other sample point. After the polygons are created, neighbors of a sample point are defined as any other sample point whose polygon shares a border with the chosen sample point. For example, in the following figure, the bright green sample point is enclosed by a polygon, which has been highlighted in red. Every location within the red polygon is closer to the bright green sample point than to any other sample point (given as small dark blue dots). The blue polygons all share a border with the red polygon, so the sample points within the blue polygons are neighbors of the bright green sample point.
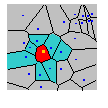
Using this definition of neighbors, a variety of local statistics can be computed. For example, a local mean is computed by taking the average of the sample points in the red and blue polygons. This average is then assigned to the red polygon. This process is repeated for all polygons and their neighbors, and the results are shown using a color ramp to help visualize regions of high and low local values.
The Voronoi Map tool provides the following methods to assign or calculate values for the polygons.
- Simple: The value assigned to a polygon is the value recorded at the sample point within that polygon.
- Mean: The value assigned to a polygon is the mean value that is calculated from the polygon and its neighbors.
- Mode: All polygons are categorized using five class intervals. The value assigned to a polygon is the mode (most frequently occurring class) of the polygon and its neighbors.
- Cluster: All polygons are categorized using five class intervals. If the class interval of a polygon is different from each of its neighbors, the polygon is colored gray and put into a sixth class to distinguish it from its neighbors.
- Entropy: All polygons are categorized using five classes based on a natural grouping of data values (smart quantiles). The value assigned to a polygon is the entropy that is calculated from the polygon and its neighbors—that is,
where pi is the proportion of polygons that are assigned to each class. For example, consider a polygon surrounded by four neighbors (a total of five polygons). The values are placed into the corresponding classes:Entropy = - Σ (pi * Log pi ),
| Class | Frequency | Pi |
|---|---|---|
1 | 3 | 3/5 |
2 | 0 | 0 |
3 | 1 | 1/5 |
4 | 0 | 0 |
5 | 1 | 1/5 |
The entropy assigned to the polygon will be
E = -[0.6*log2 (0.6) + 0.2* log2 (0.2) + 0.2* log2 (0.2)] = 1.371Minimum entropy occurs when the polygon values are all located in the same class. Then,
Emin = -[1 * log2 (1)] = 0Maximum entropy occurs when each polygon value is located in a different class interval. Then,
Emax = -[0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2)] = 2.322- Median: The value assigned to a polygon is the median value calculated from the frequency distribution of the polygon and its neighbors.
- Standard Deviation: The value assigned to a polygon is the standard deviation that is calculated from the polygon and its neighbors.
- Interquartile Range: The first and third quartiles are calculated from the frequency distribution of a polygon and its neighbors. The value assigned to the polygon is the interquartile range calculated by subtracting the value of the first quartile from the value of the third quartile.
The Voronoi statistics can be used for different purposes and can be grouped into the following general functional categories:
| Functional category | Voronoi statistics |
|---|---|
Local Smoothing | Mean, Mode, Median |
Local Variation | Standard deviation, Interquartile range, Entropy |
Local Outliers | Cluster |
Local Influence | Simple |