Disponible con una licencia de Spatial Analyst.
La herramienta Pendiente identifica la inclinación en cada celda de una superficie de ráster. Mientras menor sea el valor de la pendiente, más plano será el terreno; mientras más alto sea el valor de la pendiente, más empinado será el terreno.
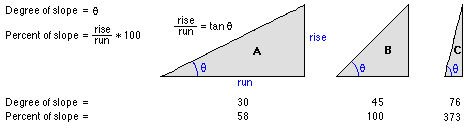
El ráster de pendiente de salida se puede calcular en dos tipos de unidades: grados o porcentaje (elevación en porcentaje). La elevación en porcentaje puede comprenderse mejor si se considera como la elevación dividida entre el avance, multiplicada por 100. Considere el triángulo B más abajo. Cuando el ángulo es de 45 grados, la elevación es igual al avance, y la elevación en porcentaje es 100%. A medida que la pendiente alcanza la vertical (90 grados), como se puede ver en el triángulo C, la elevación en porcentaje comienza a acercarse al infinito.
La herramienta Pendiente se ejecuta con más frecuencia en un dataset de elevación, tal y como se muestra en las siguientes imágenes. Las pendientes más empinadas están sombreadas en rojo en el ráster de pendiente de salida.
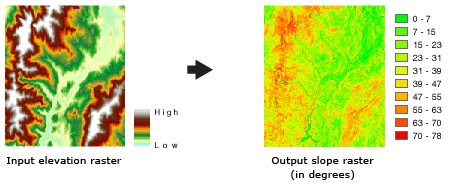
La herramienta también se puede utilizar con otros tipos de datos continuos, como la población, para identificar cambios marcados en el valor.
Métodos de cálculo y el efecto del borde
Para calcular la pendiente hay dos métodos disponibles. Puede elegir entre realizar cálculos Planares o Geodésicos con el parámetro de Método.
Para el método planar, la pendiente se mide como la tasa máxima de cambio del valor de una celda a sus vecinas inmediatas. El cálculo se realiza en un plano liso proyectado utilizando un sistema de coordenadas cartesianas 2D. El valor de la pendiente se calcula utilizando la técnica de promedio máximo (Burrough, 1998).
Con el método geodésico, el cálculo se realizará en un sistema de coordenadas cartesianas 3D teniendo en cuenta la forma de la Tierra como un elipsoide. El valor de la pendiente se calcula midiendo el ángulo entre la superficie topográfica y el datum de referencia.
Tanto los cálculos planares como geodésicos se realizan utilizando una vecindad de celdas de 3 x 3 (ventana móvil). Para cada vecindad, si la celda de procesamiento (central) es NoData, la salida es no NoData. El cálculo también requiere que al menos siete celdas vecinas a la celda de procesamiento sean válidas. Si hay menos de siete celdas válidas, el cálculo no se realizará y la salida en esa celda de procesamiento será NoData.
Las celdas de las filas y columnas más exteriores del ráster de salida serán NoData. Esto se debe a que esas celdas no tienen suficientes vecinos válidos a lo largo del límite del dataset de entrada.
Método planar
Para cada celda, la herramienta calcula la tasa máxima de cambio del valor de esa celda respecto a sus vecinas. Básicamente, el cambio máximo en la elevación sobre la distancia entre la celda y sus ocho vecinas identifica el descenso cuesta abajo más empinado desde la celda.
Algoritmo de pendiente planar
Las tasas de cambio (delta) de la superficie en las direcciones horizontal (dz/dx) y vertical (dz/dy) desde la celda central determinan la pendiente. El algoritmo básico utilizado para calcular la pendiente es el siguiente:
slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )Por lo general, la pendiente se mide en grados, y se utiliza este algoritmo:
slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578El algoritmo de pendiente también se puede interpretar de la siguiente manera:
slope_degrees = ATAN (rise_run) * 57.29578- donde:
rise_run = √ ([dz/dx]2 + [dz/dy]2]
Los valores de la celda central y sus ocho vecinas determinan las deltas horizontal y vertical. Las vecinas se identifican como letras, de la a a la i, con la letra e representando a la celda para la cual se calcula la orientación.
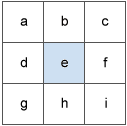
La tasa de cambio en la dirección x de la celda e se calcula con el siguiente algoritmo:
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)- donde:
wght1 y wght2 son los recuentos ponderados horizontales de las celdas válidas.
Por ejemplo, si:
- c, f e i tienen valores válidos, wght1 = (1+2*1+1) = 4.
- i es NoData, wght1 = (1+2*1+0) = 3.
- f es NoData, wght1 = (1+2*0+1) = 2.
Se aplica una lógica similar a wght2, salvo que las ubicaciones vecinas sean a, d y g.
La tasa de cambio en la dirección y de la celda e se calcula con el siguiente algoritmo:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize)- donde:
wght3 y wght4 son el mismo concepto que en cálculo de [dz/dx].
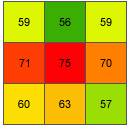
Ejemplo de cálculo de pendiente planar
En este ejemplo, se calcula el valor de la pendiente de la celda central de la ventana móvil.
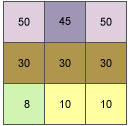
La tasa de cambio en la dirección x de la celda central e es:
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize) = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5) = (120 - 118) / 40 = 0.05La tasa de cambio en la dirección y de la celda e es:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize) = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5) = (38 - 190 ) / 40 = -3.8Tomando la tasa de cambio en la dirección x e y, la pendiente de la celda central e se calcula utilizando:
rise_run = √ ([dz/dx]2 + [dz/dy]2) = √ ((0.05)2 + (-3.8)2) = √ (0.0025 + 14.44) = 3.80032 slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762El valor de la pendiente en número entero para la celda e es 75 grados.
Método geodésico
El método geodésico mide la pendiente en un sistema de coordenadas 3D geocéntricas, también llamado sistema de coordenadas centrado en la Tierra, Tierra fija (ECEF), teniendo en cuenta la forma de la Tierra como un elipsoide. La forma en que esté proyectado el dataset no afectará al resultado del cálculo. Se utilizarán las unidades z del rásteres de entrada si están definidas en la referencia espacial. Si la referencia espacial de la entrada no define las unidades z, deberá hacerlo con el parámetro de unidad z. El método geodésico produce una pendiente más exacta que el método planar.
Transformación de coordenadas geodésicas
El sistema de coordenadas de ECEF es un sistema de coordenadas cartesianas dextrógiro 3D cuyo origen es el centro de la Tierra, donde cualquier ubicación se representa mediante coordenadas X, Y y Z. Consulte la figura siguiente para ver un ejemplo de una ubicación de destino T expresada con coordenadas geocéntricas.
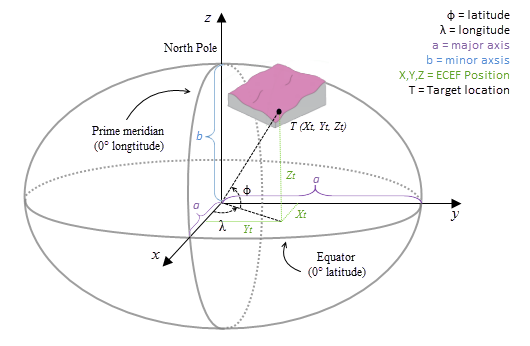
El cálculo geodésico utiliza una coordenada X, Y, Z que se calcula según sus coordenadas geodésicas (latitud φ, longitud λ, altura h). Si el sistema de coordenadas del ráster de superficie de entrada es un sistema de coordenadas proyectadas (PCS), el ráster se reproyecta primero a un sistema de coordenadas geográficas (GCS) donde cada ubicación tiene una coordenada geodésica y, a continuación, se transforma en el sistema de coordenadas de ECEF. La altura h (valor z) es la altura de elipsoide asociada a la superficie de elipsoide. Consulte el gráfico de la ilustración a continuación.
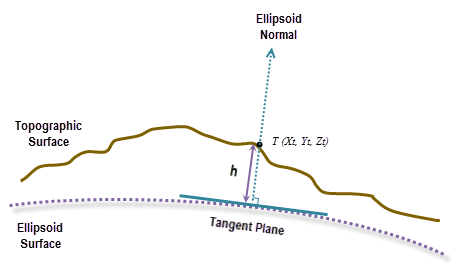
Para transformar a coordenadas de ECEF desde una coordenada geodésica (latitud φ, longitud λ, altura h), utilice las fórmulas siguientes:
X = (N(φ)+h)cosφcosλY = (N(φ)+h)cosφsinλZ = (b2/a2*N(φ)+h)sinφ- donde:
- N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
- φ = latitud
- λ = longitud
- h = altura de elipsoide
- a = eje mayor del elipsoide
- b = eje menor del elipsoide
La altura h de elipsoide se expresa en metros en las fórmulas anteriores. Si la unidad z de su ráster de entrada se especifica en otra unidad, se transformará internamente a metros.
Cálculo de pendiente
La pendiente geodésica es el ángulo formado entre la superficie topográfica y la superficie del elipsoide. Toda superficie paralela a la superficie del elipsoide tiene una pendiente de 0. Para calcular la pendiente en cada ubicación, se ajusta un plano vecino con celdas de 3 x 3 alrededor de cada celda de procesamiento utilizando el método por mínimos cuadrados. El mejor ajuste en el método por mínimos cuadrados minimiza la suma de la diferencia cuadrada (dzi) entre el valor z real y el valor z ajustado. Consulte la ilustración a continuación para ver un ejemplo.
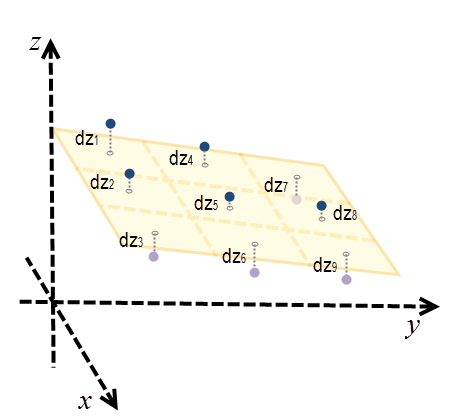
Aquí, el plano se representa como z = Ax + By + C. Para cada centro de celda, dzi es la diferencia entre el valor z real y el valor z ajustado.
El plano se ajusta mejor cuando ∑9i=1dzi2 se minimiza.
Una vez ajustado el plano, se calcula una superficie normal en la ubicación de la celda. En la misma ubicación, también se calcula un elipsoide normal perpendicular al plano tangente de la superficie de elipsoide.
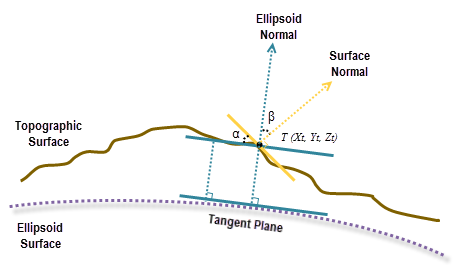
La pendiente, en grados, se calcula desde el ángulo entre la elipsoide normal y la superficie normal topográfica, representada aquí como β. Según la ilustración de arriba, el ángulo α es la pendiente geodésica, que es igual que el ángulo β, según la ley de geometría congruente.
Para calcular la pendiente como elevación en porcentaje, se utiliza la fórmula siguiente:
Slope_PercentRise = ATAN(β) * 100%Utilización de una GPU
Para el método geodésico, esta herramienta es capaz de aumentar el rendimiento si tiene determinado hardware de GPU instalado en su sistema. Consulte la sección Procesamiento de GPU con Spatial Analyst para obtener más información sobre la compatibilidad, cómo configurarla y cómo activarla.
Referencias
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Sección 10.2.1. p. 282.
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.