La herramienta Promedio de vecinos más cercanos mide la distancia entre cada centroide de entidad y la ubicación del centroide de su vecino más cercano. A continuación calcula el promedio de todas las distancias de vecinos más próximos. Si la distancia promedio es menor que el promedio de una distribución hipotética aleatoria, se considera que la distribución de las entidades que se analiza es agrupada. Si la distancia promedio es mayor que la distribución hipotética aleatoria, se considera que las entidades están dispersas. La relación de vecino más cercano promedio se calcula como la distancia promedio observada dividida por la distancia promedio esperada (con la distancia promedio esperada basada en una distribución hipotética aleatoria con el mismo número de entidades que cubren la misma área total).
Cálculos

Interpretación
Si el índice (relación de vecino más cercano promedio) es menor que 1, el patrón exhibe un clustering. Si el índice es mayor que 1, la tendencia es la dispersión.
Las ecuaciones que se utilizan para calcular el índice de la distancia promedio de vecinos más cercanos (1) y la puntuación z (4) se basan en la suposición de que los puntos que se miden son libres para ubicarse en cualquier lugar del área de estudio (por ejemplo, no existen barreras y todos los casos o las entidades se ubican de forma independiente entre sí). El valor P es una aproximación numérica del área debajo de la curva de una distribución conocida, limitada por la estadística de prueba. Consulte ¿Qué es una puntuación z? ¿Qué es un valor P? para obtener más información acerca de estas estadísticas.
Salida
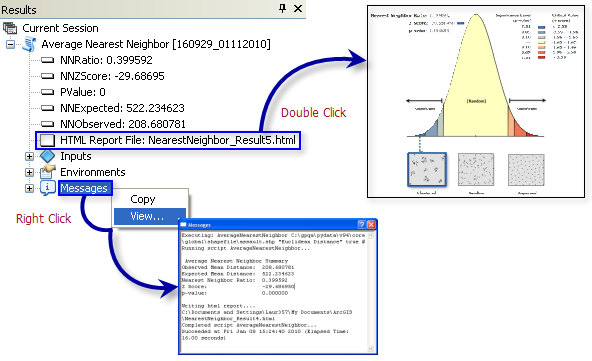
La herramienta Promedio de vecinos más cercanos devuelve cinco valores: la distancia media observada, la distancia media esperada, el índice de vecino más próximo, la puntuación z y el valor P. Se puede acceder a estos valores en la ventana Resultados y los mismos también se transmiten como valores de salida derivados para uso potencial en modelos o secuencias de comandos. Opcionalmente, esta herramienta creará un archivo HTML con un resumen gráfico de los resultados. Haga doble clic en el archivo HTML de la ventana Resultados para abrir el archivo HTML en el navegador de Internet predeterminado. Haga clic con el botón derecho del ratón en la entrada Mensajes de la ventana Resultados y seleccione Ver para mostrar los resultados en el cuadro de diálogo Mensaje.
Aplicaciones posibles
- Evaluar la competencia o el territorio: cuantifique y compare la distribución espacial de una variedad de especies de animales o plantas dentro de un área de estudio fija; compare las distancias del promedio de vecinos más cercanos para distintos tipos de negocios dentro de una ciudad.
- Controlar los cambios que se producen en el transcurso del tiempo: evalúe los cambios que se producen en el transcurso del tiempo en un clustering espacial para un tipo de negocio único dentro de un área de estudio fija.
- Comparar una distribución observada con una distribución controlada: en un análisis de árboles, es probable que desee comparar el patrón de las áreas cosechadas con el patrón de las áreas cosechables para determinar si las áreas de corte están más agrupadas de lo esperado, dada la distribución general de árboles cosechables.
Recursos adicionales
Los siguientes libros incluyen más información sobre esta herramienta:
Ebdon, David. Estadísticas en Geografía. Blackwell, 1985.
Mitchell, Andy. La Guía de Esri para el análisis SIG, Volumen 2. Esri Press, 2005.