La salida generada por la herramienta de regresión de OLS, sigla de Ordinary Least Squares (Mínimos cuadrados ordinarios), incluye lo siguiente:
- Clase de entidad de salida
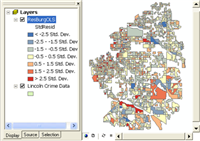
Mapa de residuales de OLS - Informe de los resultados estadísticos de la ventana Mensaje
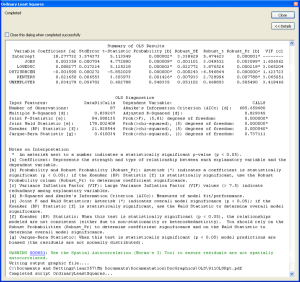
Informe estadístico de OLS - Archivo de informe PDF opcional
- Tabla opcional de coeficientes de variable explicativa
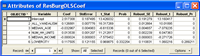
Tabla de coeficiente de los resultados del modelo OLS - Tabla opcional de diagnósticos de regresión
Tabla de diagnósticos del modelo OLS
Cada una de estas salidas se muestra y se describe a continuación como una serie de pasos para ejecutar la regresión de OLS e interpretar sus resultados.
(A) Para ejecutar la herramienta OLS, proporcione una Clase de entidad de entrada con un Campo de Id. único, la Variable dependiente que desea modelar/explicar/predecir y una lista de Variables explicativas. También deberá proporcionar una ruta para la Clase de entidad de salida y, de manera opcional, las rutas del Archivo del informe de salida, la Tabla de salida de coeficiente y la Tabla de salida de diagnóstico.
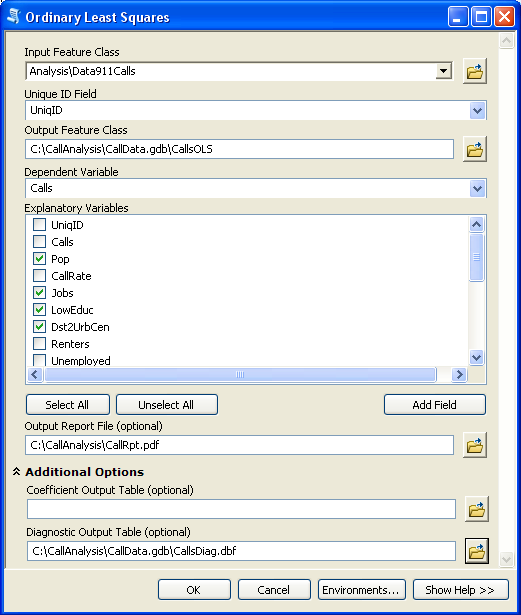
Después de ejecutar OLS, lo primero que se recomienda hacer es consultar el informe de resumen de OLS, que se escribe en forma de mensajes durante la ejecución de la herramienta y se guarda también como archivo de informe si se proporciona una ruta para el parámetro Archivo de informe de salida.
(B) Examine el informe de resumen siguiendo los pasos numerados que se describen a continuación:
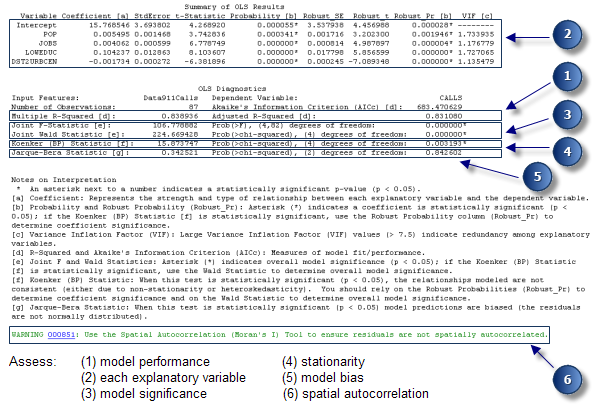
Dividir el informe estadístico
- Evaluación del rendimiento del modelo. Los valores R cuadrado múltiple y R cuadrado ajustado son medidas del rendimiento del modelo. Los valores posibles varían de 0,0 a 1,0. El valor R cuadrado ajustado siempre es un poco más bajo que el valor R cuadrado múltiple, porque refleja la complejidad del modelo (la cantidad de variables) ya que se relaciona con los datos y es, por lo tanto, una medida más exacta del rendimiento del modelo. Si se agrega una variable explicativa adicional al modelo, probablemente el valor R cuadrado múltiple aumente y el valor R cuadrado ajustado disminuya. Supongamos que está creando un modelo de regresión de robo residencial (la cantidad de robos residenciales asociados con cada bloque censal es la variable dependiente, y). Un valor R cuadrado ajustado de 0,39 indicará que el modelo (sus variables explicativas modeladas con una regresión lineal) explica aproximadamente el 39 por ciento de la variación en la variable dependiente. Dicho de otra manera, su modelo cuenta aproximadamente el 39 por ciento de la historia de robo residencial.

Los valores R cuadrado cuantifican el rendimiento del modelo - Evaluación de cada variable explicativa en el modelo: coeficiente, probabilidad o probabilidad robusta y Factor de inflación de la varianza (VIF). El coeficiente para cada variable explicativa refleja la fuerza y el tipo de relación que tiene la variable explicativa con la variable dependiente. Cuando el signo asociado con el coeficiente es negativo, la relación es negativa (por ejemplo, cuanto mayor la distancia desde un núcleo urbano, menor la cantidad de robos residenciales). Cuando el signo es positivo, la relación es positiva (por ejemplo, cuanto mayor la población, mayor la cantidad de robos residenciales). Los coeficientes se proporcionan en las mismas unidades que sus variables explicativas asociadas (un coeficiente de 0,005 asociado con una variable que representa el conteo de población puede interpretarse como 0,005 personas). El coeficiente refleja el cambio esperado en la variable dependiente para cada cambio en una unidad en la variable explicativa asociada, manteniendo todas las otras variables constantes (por ejemplo, se espera un incremento de 0,005 en el robo residencial por cada persona adicional en el bloque censal, manteniendo todas las otras variables explicativas constantes). La prueba T se utiliza para evaluar si una variable explicativa es estadísticamente significativa o no. La hipótesis nula es que el coeficiente es, en todos sus propósitos, igual a cero (y, como consecuencia, no ayuda al modelo). Cuando la probabilidad o la probabilidad robusta (valor p) es muy pequeña, la posibilidad de que el coeficiente sea esencialmente cero también es pequeña. Si la prueba Koenker (ver abajo) es estadísticamente significativa, utilice las probabilidades robustas para evaluar la importancia estadística de la variable explicativa. Las probabilidades estadísticamente significativas tienen un asterisco (*) junto a ellas. Una variable explicativa asociada con un coeficiente estadísticamente significativo es importante para el modelo de regresión si la teoría o el sentido común admite una relación válida con la variable dependiente, si la relación modelada es principalmente lineal, y si la variable no es redundante para ninguna otra variable explicativa en el modelo. La VIF mide la redundancia entre las variables explicativas. Como regla práctica, las variables explicativas asociadas con los valores del VIF mayores que 7,5 aproximadamente deben quitarse (de a uno por vez) del modelo de regresión. Si, por ejemplo, tiene una variable de población (el número de personas) y una variable de empleo (el número de personas con empleo) en el modelo de regresión, probablemente descubrirá que están asociadas con valores del VIF altos que indican que ambas variables están proporcionando la misma información, y deberá quitar una del modelo.
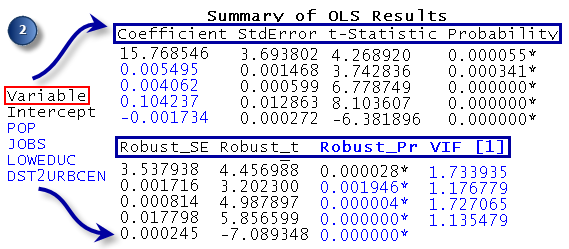
Evalúe qué variables son estadísticamente significativas. - Evaluación de la importancia del modelo. Tanto el el índice estadístico F conjunto como el índice estadístico de Wald conjunto son medidas de la importancia estadística general del modelo. El índice estadístico F conjunto es confiable únicamente cuando el índice estadístico de Koenker (BP) (ver abajo) no es estadísticamente significativo. Si el índice estadístico de Koenker (BP) es significativo, debe consultar el índice estadístico de Wald conjunto para determinar la importancia general del modelo. La hipótesis nula para estas dos pruebas es que las variables explicativas del modelo no son efectivas. Para un nivel de confianza del 95 por ciento, un valor p (probabilidad) menor que 0,05 indica un modelo estadísticamente significativo.
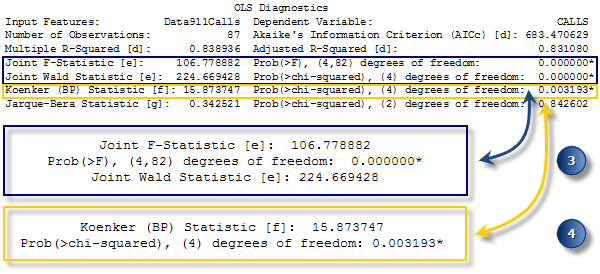
Evaluación de la importancia estadística general del modelo de regresión. - Evaluación de la estacionariedad. El índice estadístico de Koenker (BP) (índice estadístico de Breusch-Pagan estudentizado de Koenker) es una prueba para determinar si las variables explicativas del modelo tienen una relación consistente con la variable dependiente, tanto en el espacio geográfico como en el espacio de datos. Cuando el modelo es consistente en el espacio geográfico, los procesos espaciales representados por las variables explicativas se comportan de la misma manera en cualquier parte del área de estudio (los procesos son estacionarios). Cuando el modelo es consistente en el espacio de datos, la variación en la relación entre los valores previstos y cada variable explicativa no cambia cuando cambian las magnitudes de la variable explicativa (no hay heterocedasticidad en el modelo). Supongamos que quiere prever el crimen y una de sus variables explicativas es el ingreso. El modelo tendrá una heterocedasticidad problemática si las predicciones fueron más exactas para las ubicaciones con ingresos medios bajos que para las ubicaciones con ingresos medios altos. La hipótesis nula para esta prueba es que el modelo es estacionario. Para un nivel de confianza del 95 por ciento, un valor p (probabilidad) menor que 0,05 indica una heterocedasticidad o no estacionariedad estadísticamente significativa. Cuando los resultados de esta prueba sean estadísticamente significativos, consulte los errores y las probabilidades estándar del coeficiente robusto para evaluar la efectividad de cada variable explicativa. Los modelos de regresión con no estacionariedad estadísticamente significativa a veces son buenos candidatos para el análisis de Regresión ponderada geográficamente (GWR).
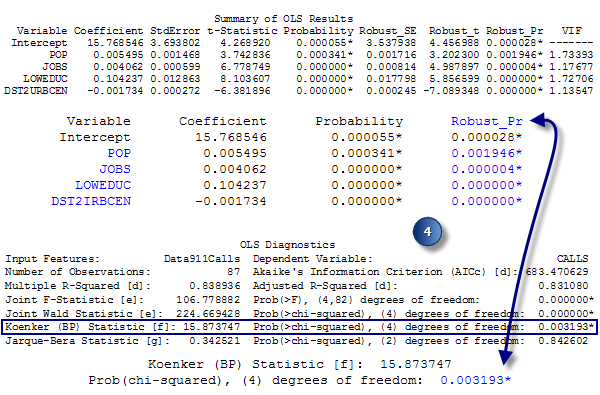
Evaluación de la estacionariedad: si la prueba de Koenker es estadísticamente significativa (*), consulte las probabilidades robustas para determinar si los coeficientes de la variable explicativa son significativos o no. - Evaluación de la influencia del modelo. El índice estadístico de Jarque-Bera indica si los residuales (los valores de la variable dependiente observada o conocida menos los valores previstos o estimados) se distribuyen normalmente o no. La hipótesis nula para esta prueba es que los residuales son distribuidos normalmente, por lo tanto, si construyera un histograma de dichos residuales, se parecerían a la curva de Bell o a la distribución gaussiana. Cuando el valor p (probabilidad) de esta prueba es bajo (menor que 0,05 para un nivel de confianza del 95 por ciento, por ejemplo), los residuales no son distribuidos normalmente, lo que indica que el modelo es tendencioso. Si también cuenta con una autocorrelación espacial estadísticamente significativa de los residuales (ver abajo), la influencia puede ser el resultado de una especificación incorrecta del modelo (una variable clave está faltando en el modelo). Los resultados de un modelo de OLS con especificación incorrecta no son confiables. También puede producirse una prueba de Jarque-Bera estadísticamente significativa si intenta modelar relaciones no lineales, si los datos incluyen valores atípicos influyentes o cuando hay una heterocedasticidad elevada.
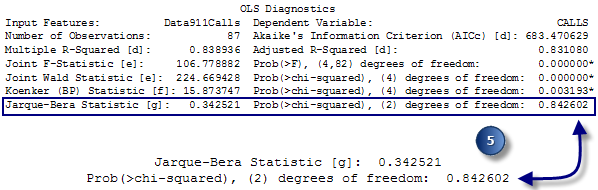
Evaluación de la influencia del modelo. - Evaluación de la autocorrelación espacial residual. Siempre ejecute la herramienta Autocorrelación espacial (I de Moran) en los residuales de regresión para asegurarse de que son espacialmente aleatorios. El clustering estadísticamente significativo de los residuales altos o bajos (predicciones altas o bajas del modelo) indica que falta una variable clave en el modelo (especificación incorrecta). Los resultados de OLS no serán fiables si el modelo se ha especificado de una forma incorrecta.

Utilice la herramienta Autocorrelación espacial para asegurarse de que los residuales del modelo no estén autocorrelacionados espacialmente. - Finalmente, revise la sección con el título Cómo dejan de funcionar los modelos de regresión en el documento Conceptos básicos del análisis de regresión para verificar que el modelo de regresión de OLS esté especificado correctamente. Si tiene problema para encontrar un modelo de regresión especificado correctamente, la herramienta Regresión exploratoria puede ser muy útil. Las Notas sobre la interpretación al final del informe de resumen de OLS están ahí para ayudarle a recordar el propósito de cada prueba estadística y guiarle hacia una solución cuando el modelo falla uno o más de los diagnósticos.

El informe de OLS incluye notas para ayudarlo a interpretar la salida del diagnóstico.
(C) Si proporciona una ruta para el Archivo de informe de salida opcional, se creará un PDF que contenga toda la información en el informe de resumen más gráficos adicionales para ayudarlo a evaluar su modelo. La primera página del informe proporciona información sobre cada variable explicativa. De manera similar a la primera sección del informe de resumen (consulte el número 2 de arriba) podría utilizar la información que aparece aquí para determinar si los coeficientes de cada variable explicativa son estadísticamente significativos y tienen el signo esperado (+/-). Si la prueba Koenker es estadísticamente significativa (consulte el número 4 de arriba), solo puede confiar en las probabilidades sólidas para decidir si una variable está ayudando a su modelo o no. Los coeficientes estadísticamente significativos tendrán un asterisco junto a sus valores p para las probabilidades y/o columnas de probabilidades sólidas. También puede decir a partir de la información en esta página del informe si cualquiera de las variables explicativas son redundantes (muestran una multicolinealidad problemática). A menos que la teoría dicte lo contrario, las variables explicativas con valores del Factor de inflación de la varianza (VIF), se deben eliminar los valores uno por uno hasta que los valores VIF para todas las variables explicativas restantes estén por debajo de 7.5.
La siguiente sección en el Archivo de informe de salida enumera los resultados de las verificaciones de diagnóstico de OLS. Esta página también incluye Notas sobre la interpretación que describen por qué cada verificación es importante. Si el modelo falla uno de estos diagnósticos, consulte la tabla de problemas comunes de regresión que describe la gravedad de cada problema y sugiere un remedio potencial. Los gráficos de las páginas restantes del informe también le ayudarán a identificar y remediar los problemas con su modelo.

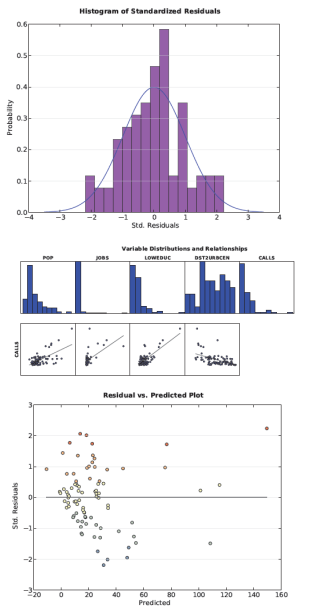
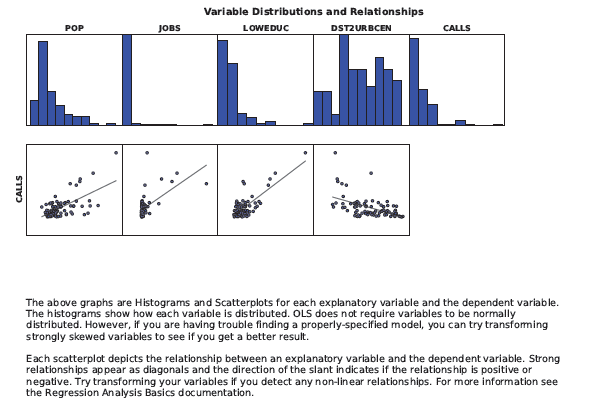
La tercera sección del Archivo del informe de salida incluye histogramas que muestran la distribución de cada variable en el modelo, y diagramas de dispersión que muestran la relación entre la variable dependiente y cada variable explicativa. Si está teniendo problema con la influencia del modelo (indicado por un valor p Jarque-Bera estadísticamente significativo), busque distribuciones sesgadas entre los histogramas, e intente transformar estas variables para ver si esto elimina la influencia y mejora el rendimiento del modelo. Los diagramas de dispersión le muestran qué variables son los mejores indicadores. Utilice estos gráficos de dispersión para buscar también relaciones no lineales entre sus variables. En algunos casos, la transformación de una o más variables arreglará las relaciones no lineales y eliminará la influencia del modelo. Los Valores atípicos en los datos también pueden resultar en un modelo sesgado. Marque los histogramas y los diagramas de dispersión de estos valores de datos y/o las relaciones de los datos. Intente ejecutar el modelo con y sin un valor atípico para ver cuánto está afectando los resultados. Es posible que descubra que el valor atípico tiene datos no válidos (escritos o registradas en error) y poder eliminar la entidad asociada del dataset. Si el valor atípico refleja datos válidos y está teniendo un impacto muy fuerte sobre los resultados de su análisis, puede decidir informar sus resultados tanto con y sin el valor atípico(s).
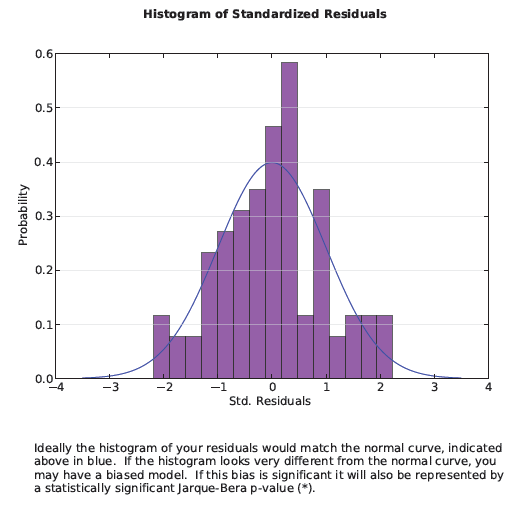
Cuando tiene un modelo especificado correctamente, las predicciones escasas y excesivas reflejarán ruido aleatorio. Si fuera a crear un histograma de ruido aleatorio, estaría normalmente distribuido (piense en la curva de Bell). La cuarta sección del Archivo del informe de salida presenta un histograma de las predicciones escasas y excesivas del modelo. Las barras del histograma muestran la distribución real, y la línea azul superpuesta sobre el histograma muestra la forma que tendría el histograma si los residuales, de hecho, se distribuyeran normalmente. La perfección es poco probable, así que querrá revisar la prueba Jarque-Bera para determinar si la desviación de una distribución normal es estadísticamente significativa o no.
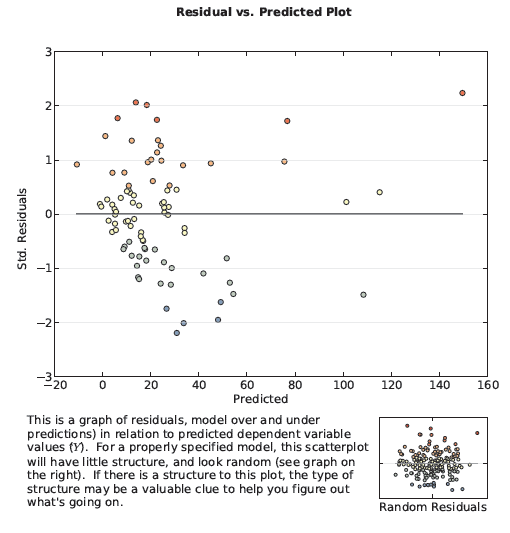
El diagnóstico de Koenker le indica si las relaciones que está modelando cambian en el área de estudio (no estacionariedad) o variar en relación con la magnitud de la variable que intenta prever (heteroscedasticidad). Regresión ponderada geográficamente resolverá los problemas con la no estacionariedad; el gráfico de la sección 5 del Archivo del informe de salida indicará si hay algún problema con la heterocedasticidad. Este gráfico del diagrama de dispersión (se muestra a continuación) grafica la relación entre los residuales del modelo y los valores previstos. Supongamos que modela las tasas de delincuencia. Si el gráfico revela una forma de cono con el punto en la izquierda y la difusión más amplia en el lado derecho del gráfico, indica que el modelo está haciendo buenas predicciones en ubicaciones con bajos índices de delincuencia, pero no las está haciendo bien en ubicaciones con altos índices de delincuencia.
La última página del informe registra toda la configuración del parámetro que se utilizaron cuando se creó el informe.
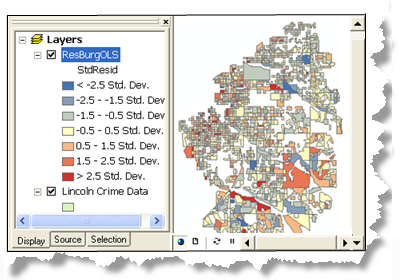
(D) Examine los residuales del modelo que se encuentran en la Clase de entidad de salida. Las predicciones escasas y excesivas para un modelo de regresión especificado correctamente se distribuirán aleatoriamente. El clustering de predicción excesiva o escasa es evidencia de que falta al menos una variable explicativa clave. Examine los patrones en los residuales del modelo para determinar si proporcionan pistas acerca de qué pueden ser esas variables que faltan. A veces, ejecutar el Análisis de punto caliente en los residuales de regresión le ayuda a identificar los patrones más amplios. Las estrategias adicionales para hacer frente a un modelo incorrectamente especificado se describen en ¿Qué es lo que no le dicen sobre el análisis de regresión?
(E) Vea las tablas de diagnóstico y de coeficientes. La creación de las tablas de diagnóstico y de coeficientes es opcional. Mientras esté buscando un modelo efectivo, puede elegir no crear estas tablas. El proceso de construcción del modelo es iterativo, y probablemente probará una gran cantidad de modelos diferentes (variables explicativas diferentes) hasta que encuentre algunos buenos. Puede utilizar el Criterio de información de Akaike corregido (AICc) en el informe para comparar diferentes modelos. El modelo con el valor del AICc más pequeño es el mejor (es decir, teniendo en cuenta la complejidad del modelo, el modelo con el AICc más pequeño se ajusta mejor a los datos observados).
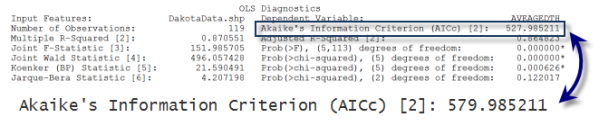
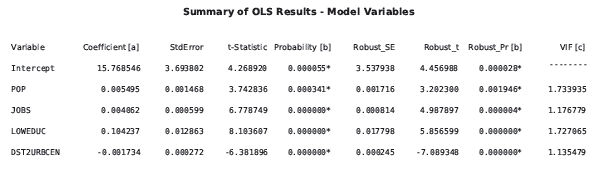
La creación de tablas de diagnóstico y de coeficientes para los modelos de OLS finales permite capturar elementos importantes del informe de OLS. La tabla de coeficientes incluye la lista de variables explicativas utilizadas en el modelo con sus coeficientes, coeficientes estandarizados, errores estándar y probabilidades. El coeficiente es una estimación de la medida en que la variable dependiente cambiaría en caso de producirse un cambio de 1 unidad en la variable explicativa asociada. Las unidades de los coeficientes coinciden con las variables explicativas. Si, por ejemplo, cuenta con una variable explicativa para la población total, las unidades de coeficiente para esa variable indican personas; si otra variable explicativa es la distancia en metros desde la estación de tren, las unidades de coeficiente indican metros. Cuando los coeficientes se convierten a desviaciones estándar, se denominan coeficientes estandarizados. Los coeficientes estandarizados se pueden usar para comparar el efecto que distintas variables explicativas ejercen sobre la variable dependiente. La variable explicativa con el mayor coeficiente estandarizado después de eliminar el signo +/- (toma el valor absoluto) tiene el mayor efecto en la variable dependiente. Sin embargo, las interpretaciones de los coeficientes solo se pueden realizar en función del error estándar. Los errores estándar indican la probabilidad que tiene de obtener los mismos coeficientes si pudiera remuestrear los datos y recalibarar el modelo un número infinito de veces. Los errores estándar grandes para un coeficiente indican que el proceso de remuestreo tendría como resultado un amplio rango de valores de coeficiente; los errores estándar pequeños indican que el coeficiente sería bastante coherente.
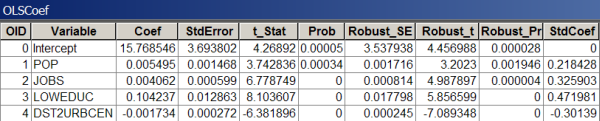
La tabla de diagnóstico incluye los resultados de cada prueba de diagnóstico junto con algunas pautas para interpretar dichos resultados.

Recursos adicionales
Existen varios recursos buenos para ayudarlo a obtener más información sobre la regresión de OLS en la página Recursos de estadística espacial. Comience leyendo la documentación Conceptos básicos del análisis de regresión o viendo el vídeo sobre conceptos básicos del análisis de regresión. Después, consulte un Tutorial de análisis de regresión. Aplicar el análisis de regresión a sus propios datos, refiriéndose a la tabla de problemas comunes y el artículo llamado Lo que no le dicen sobre el análisis de regresión para estrategias adicionales. Si tiene problema para encontrar un modelo especificado correctamente, la herramienta Regresión exploratoria puede ser muy útil.