La herramienta Análisis clúster espacial de distancia múltiple, que se basa en la Función K de Ripley, es otra forma de analizar el patrón espacial de los datos de puntos del incidente. Una característica que distingue este método de otros en este conjunto de herramientas (Autocorrelación espacial y Análisis de punto caliente) es que resume la dependencia espacial (clustering de entidad o dispersión de entidad) en un rango de distancias. En varios estudios de análisis de patrón de entidad, se requiere la selección de una escala apropiada de análisis. Por ejemplo, a veces se necesita una Banda de distancia o distancia de umbral para el análisis. Cuando se exploran patrones espaciales en distancias múltiples y escalas espaciales, los patrones cambian y a veces reflejan el dominio de procesos espaciales particulares en el trabajo. La Función K de Ripley ilustra cómo cambia el clustering espacial o la dispersión de los centroides de la entidad cuando cambia el tamaño de la vecindad.
Cuando utilice esta herramienta, especifique la cantidad de distancias a evaluar y, opcionalmente, una distancia de inicio y/o incremento de distancia. Con esta información, la herramienta calcula la cantidad promedio de entidades vecinas asociadas con cada entidad; las entidades vecinas son aquellas que están más cerca que la distancia que se evalúa. A medida que aumenta la distancia de evaluación, cada entidad tendrá por lo general más vecinos. Si la cantidad promedio de vecinos para una distancia de evaluación particular es más alta/más grande que la concentración promedio de entidades a través del área de estudio, la distribución se considera agrupada a esa distancia.
Utilice esta herramienta cuando desee examinar cómo cambia el clustering/dispersión de las entidades en distintas distancias (distintas escalas de análisis).
Cálculos
Se sugirió una cantidad de variaciones de la Función K original de Ripley. Aquí, se implementa una transformación común de la Función K, que a veces se denomina L(d):

Los valores predeterminados de Distancia de inicio e Incremento de distancia se calculan de la siguiente manera:
- Siempre sabemos cuál es la Cantidad de bandas de distancia (el valor predeterminado es 10). Utilizaremos este valor de Iteraciones para calcular un Incremento de distancia predeterminado si no se ha proporcionado ninguno.
- Inicialmente calculamos un valor Distancia máxima como un 25 por ciento de la longitud de extensión máxima de un rectángulo mínimo envolvente alrededor de entidades de entrada. Si el Método de corrección de límite es REDUCE_ANALYSIS_AREA, la Distancia máxima se establece en el 25 por ciento de la longitud de extensión máxima o en el 50 por ciento de la longitud de extensión mínima de un rectángulo mínimo envolvente, el valor que sea mayor de los dos.
- Si se proporciona una Distancia de inicio, el Incremento de distancia es (Distancia máxima - Distancia de inicio) / Iteraciones.
- Si no se proporciona una Distancia de inicio, el Incremento de distancia es Distancia máxima / Iteraciones y la Distancia de inicio se establece en el valor de Incremento de distancia.
Interpretar los resultados de la Función K no ponderada
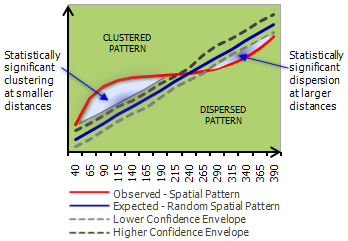
Cuando el valor K observado es mayor que el valor K esperado para una distancia particular, la distribución es más agrupada que una distribución aleatoria en esa distancia (escala de análisis). Cuando el valor K observado es menor que el valor K esperado, la distribución es más dispersa que una distribución aleatoria en esa distancia. Cuando el valor K observado es mayor que el valor superior de sobre de confianza (HiConfEnv), el clustering espacial para esa distancia es significativo desde el punto de vista estadístico. Cuando el valor K observado es menor que el valor inferior de sobre de confianza (LwConfEnv), la dispersión espacial para esa distancia es significativa desde el punto de vista estadístico.
Cuando no se especifica ningún Campo de peso, el sobre de confianza se construye al distribuir puntos aleatoriamente en el área de estudio y calcular K para esa distribución. Cada distribución aleatoria de los puntos se llama "permutación". Si se selecciona 99_PERMUTATIONS, por ejemplo, la herramienta distribuirá aleatoriamente el conjunto de puntos 99 veces para cada iteración. Después de distribuir los puntos 99 veces la herramienta selecciona, para cada distancia, el valor k que se desvió hacia arriba o hacia abajo del valor k esperado con la cantidad más grande; estos valores se convierten en el intervalo de confianza. Los sobres de confianza tienden a seguir (tienen la misma forma y ubicación) la línea K esperada azul para la K no ponderada.
Interpretar los resultados de la Función K ponderada
La Función K siempre evalúa la distribución espacial de la entidad en relación con la Aleatoriedad espacial completa (CSR), incluso aunque se indique un Campo de peso. Puede pensar que el peso representa la cantidad de entidades coincidentes en cada ubicación de entidad. Por ejemplo, una entidad con un peso de 3 se puede interpretar como 3 entidades coincidentes. Sin embargo, existe una diferencia: una entidad no puede ser su propio vecino. Por lo tanto, obtendría un resultado distinto para un dataset donde hay 3 puntos coincidentes individuales con un peso de 1 (todos se contarían como vecinos de los otros) al que obtendría para un dataset con un único punto con un peso de 3 (una entidad no se cuenta como un vecino de sí mismo). Los resultados de la Función K ponderada siempre estarán más agrupados que los resultados sin un campo de peso. Es útil ejecutar la Función K en los puntos sin un peso para obtener una línea base que indique la cantidad de clustering que se asocia con las ubicaciones de entidades solas. Después puede comparar la línea base con los resultados ponderados para obtener una idea de la cantidad de clustering o dispersión adicional que se agrega cuando se tiene en cuenta el peso. La Función K ponderada muestra el clustering (dispersión) sobre y encima (debajo) del que obtendría del patrón no ponderado. En realidad, en lugar de CSR, puede utilizar los resultados de la Función K no ponderada para representar el patrón esperado (con su propio sobre de confianza). Hay dos hipótesis nulas posibles en este caso:
- El patrón de entidades ponderadas no está significativamente más agrupado (disperso) que el patrón subyacente de esas entidades. Rechaza la hipótesis nula si los resultados ponderados observados caen fuera del sobre de confianza de los resultados no ponderados.
- El patrón de puntos ponderados está más agrupado (disperso) que la posibilidad que tendría. Rechaza la hipótesis nula si los resultados no ponderados observados caen dentro del sobre de confianza de los resultados de la función K ponderados.
Cuando se especifica un Campo de peso, solo los valores de peso se redistribuyen aleatoriamente para calcular los contornos de confianza; las ubicaciones de punto permanecen fijas. En esencia, cuando se especifica un Campo de peso, las ubicaciones permanecen fijas y la herramienta evalúa el clustering de los valores de la entidad en el espacio. Debido a que los resultados están muy estructurados por las ubicaciones fijas de las entidades, para los análisis K ponderados el sobre de confianza tiende a seguir/reflejar la línea K Observada roja.
Recursos adicionales
Bailey, T. C., y A. C. Gatrell. Interactive Spatial Data Analysis. Longman Scientific & Technical, Harlow, U.K. 395 pp. 1995.
Boots, B., y A. Getis. Point Pattern Analysis. Sage University Paper Series on Quantitative Applications in the Social Sciences, series no. 07–001. Sage Publications. 1988.
Getis, A. Interactive Modeling Using Second-Order Analysis. Environment and Planning A, 16: 173–183. 1984.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. Esri Press, 2005.