Disponible con una licencia de Spatial Analyst.
En las herramientas de coste de distancia y distancia de ruta, al definir las características de origen del objeto en movimiento se tiene control sobre lo siguiente:
- Distintos modos de viajar desde diferentes orígenes (por ejemplo, viajar en coche o caminando)
- Magnitudes en los orígenes (por ejemplo, distinto número de tropas del ejército en cada ubicación)
- Una función de decaimiento de coste (por ejemplo, un excursionista se cansa)
- El coste inicial desde un origen (por ejemplo, el tiempo que lleva poner el camión en la carretera)
- Las capacidades de los orígenes (por ejemplo, a qué distancia puede viajar un vehículo antes de quedarse sin combustible)
- La dirección de viaje del elemento que se mueve (por ejemplo, si este se aleja de un origen o se acerca a él)
Algunos problemas de ejemplo resueltos por las características del origen
A través de las características del origen puede abordar las siguientes aplicaciones adicionales de coste de distancia y distancia de ruta:
- Determine el área en la que se puede buscar a un excursionista perdido desde dos centros que tienen distintos medios de viaje (quads en un caso y a pie en el otro).
- Explore las ubicaciones hasta las que pueden llegar los bomberos desde tres parques de bomberos teniendo en cuenta el número de bomberos que hay en cada centro. Hay 25 bomberos en la primera instalación, 15 en la segunda y 10 en la tercera.
- Identifique las mejores ubicaciones para acampar teniendo en cuenta la pérdida de energía de un excursionista a medida que se cansa.
- Analice el tiempo que se tardará en llegar a un incendio en la maleza lejano teniendo en cuenta los 16 minutos que los bomberos necesitan para cargar el equipo.
- Defina dónde se deben ubicar las estaciones de repostaje de combustible para unos vehículos de suministros médicos que deben viajar una gran distancia para llegar a un objetivo lejano en una operación de ayuda humanitaria.
Fórmulas de coste de distancia que tienen en cuenta las características del origen
Las fórmulas de coste de distancia empleadas para tener en cuenta las características del origen se detallan en las siguientes secciones.
Fórmulas básicas de coste de distancia
Hay dos fórmulas básicas de coste de distancia que se pueden utilizar en función de la forma escogida para atravesar las celdas adyacentes.
Celdas perpendiculares
La fórmula de coste de distancia para las celdas perpendiculares es la siguiente:
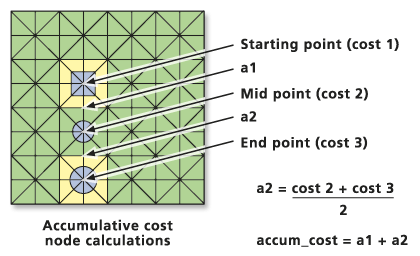
accum_cost = a1 + (cost2 + cost3)/2- Donde
a1: el coste acumulativo de la celda 1 a la celda 2
cost2: el coste de viaje de la celda 2
cost3: el coste de viaje de la celda 3
accum_cost: el coste acumulativo para moverse hasta la celda 3 desde la celda 1
Celdas diagonales
La fórmula de coste de distancia para las celdas diagonales es la siguiente:
accum_cost = a1 + (1.4142 * ((cost2 + cost3)/2))Fórmula de distancia de ruta
Hay dos fórmulas básicas de distancia de ruta que se pueden utilizar en función de la forma escogida para atravesar las celdas adyacentes.
Celdas perpendiculares
accum_cost = a1 + ((((cost2 * HF(2)) + (cost3 * HF(3)))/2) * Surface_distance(23) * VF(23))- Donde
cost2: el coste de viaje de la celda 2
cost3: el coste de viaje de la celda 3
HF(2): el factor horizontal de la celda 2
HF(3): el factor horizontal de la celda 3
Surface_distance(23): la distancia de superficie de 2 a 3
VF(23): el factor vertical de 2 a 3
Celdas diagonales
accum_cost = a1 + ((((cost2 * HF(2)) + (cost3 * HF(3)))/2) * 1.414214 * Surface_distance(23) * VF(23))Fórmulas de coste de distancia y de distancia de ruta que tienen en cuenta las características del origen
Para tener en cuenta las características del objeto en movimiento desde los orígenes se aplican las siguientes fórmulas.
Coste de distancia a las celdas perpendiculares
accum_cost = (a1 * (1.0 + resistance_rate) + (((cost2 + cost3) / 2) * cost_multiplier))- Donde
resistance_rate: un ajuste dinámico del coste acumulativo para simular una respuesta cambiante con el fin de superar las unidades de coste a medida que aumenta el coste acumulativo, por ejemplo a medida que un excursionista se cansa.
cost_multiplier: un multiplicador de las unidades de coste. Cuanto mayor sea el valor, más costoso será el movimiento, por ejemplo caminar frente a conducir un quad.
Distancia de ruta a las celdas perpendiculares
accum_cost = (a1 * (1 + resistance_rate)) + ((((cost2 * HF(2)) + (cost3 * HF(3)))/2) * Surface_distance(23) * VF(23) * cost_multiplier)Las características del origen se identifican con un solo valor, que se aplica a todos los orígenes, o con un campo de la tabla de atributos asociado con los orígenes, de modo que cada valor se aplica al origen correspondiente.
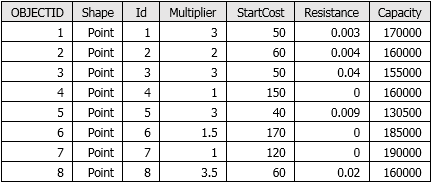
Multiplicador de coste
Caso de uso 1: diferentes modos de viaje desde cada origen, como utilizar un quad frente a caminar.
Caso de uso 2: diferente magnitud de recursos en cada origen, como un número diferente de bomberos en cada estación de bomberos.
Los distintos modos de viaje o las distintas magnitudes en un origen permiten aumentar o reducir la velocidad de movimiento o la cobertura en la superficie de coste. Estas características aumentan o reducen el coste del movimiento por una celda.
El modo o la magnitud se puede implementar por medio del multiplicador de coste. Los quad tendrían un multiplicador más bajo que andar, ya que pueden superar los costes a una velocidad mayor, mientras que más bomberos en un origen pueden tener un multiplicador más bajo que un origen con menos bomberos, ya que pueden cubrir más área (pueden superar el coste más deprisa).
Si el multiplicador es un valor único, se aplicará a todos los orígenes. Si los modos o las magnitudes (el multiplicador) varían por origen, el multiplicador se puede especificar por medio de un campo asociado con los orígenes.
Coste inicial
Caso de uso: tiempo necesario para prepararse antes de salir del origen.
Un coste inicial se puede identificar con un valor único que se sumará a cada uno de los orígenes o por medio de un campo asociado con los orígenes si los costes iniciales varían para los distintos orígenes. Estos son los costes fijos asociados con los orígenes.
Para llegar a la primera celda, en lugar de iniciar los cálculos del origen en cero usando lo siguiente
a1 = (((cost1 + cost2) / 2) * cost_multiplier)Se usa la fórmula acumulativa con starting_cost, el coste inicial asociado con el origen
a1 = starting_cost + (((cost1 + cost2) / 2) * cost_multiplier)Tasa de resistencia
Caso de uso: soy un excursionista que pierde energía.
Esta es la única característica del origen que cambia dinámicamente. A medida que aumenta el coste acumulativo, también lo hace el efecto de la tasa de resistencia. Cuando se determina el coste de moverse a la celda siguiente, conceptualmente, el coste acumulativo de llegar a la celda se multiplica por la tasa de resistencia, y el producto se suma al cálculo del coste acumulado. Como resultado, el efecto de la tasa se calcula con el viajero; por tanto, cuanto mayor sea la tasa de resistencia, mayor será el esfuerzo necesario para superar cada unidad de coste posterior: el viajero se cansa con más rapidez.
Como la tasa de resistencia es similar a una tasa compuesta y normalmente los valores de coste acumulativos son muy grandes, es recomendable usar tasas de resistencia pequeñas (por ejemplo, 0,005).
Capacidad
Caso de uso: identifique las ubicaciones potenciales para estaciones de repostaje de vehículos de suministro médico en un área remota.
Se define una capacidad de coste para cada origen (o los modos de viaje desde el origen) con un valor único o un campo. El algoritmo de coste de distancia dinámico sigue creciendo hasta que se alcanza la capacidad de cada origen. La asignación de costes resultante puede ser diferente si se define el parámetro de capacidad (frente a los casos en los que no se define). Es decir: si una región con una capacidad baja está cerca de una región con una capacidad alta, la región de alta capacidad puede capturar alguna de las celdas de la asignación original de la región de menor capacidad cuando no se ha definido ninguna capacidad (pero solo las celdas que tienen un coste acumulativo mayor que la capacidad definida para la región con menor capacidad).
Dirección del viaje
Caso de uso 1: un lince rojo prefiere, por seguridad, ubicaciones más alejadas de las carreteras.
Caso de uso 2: un lince rojo prefiere ubicaciones desde las que sea más fácil llegar a un arroyo.
Esta característica del origen permite especificar la dirección de viaje de lo que se mueve. La opción Viaje desde el origen del parámetro Dirección del viaje simula que lo que se mueve parte del origen y se desplaza hasta todas las ubicaciones que se encuentran fuera del origen. La opción Viaje hasta el origen simula que lo que se mueve parte desde todas las ubicaciones distintas del origen y vuelve al origen. La dirección del viaje afecta a todos los parámetros influidos por la dirección del viaje del elemento que se mueve. Son el coste inicial y la tasa de resistencia en Coste de distancia, Asignación de costes y Vínculo de menor coste y el coste inicial, la tasa de resistencia y los factores vertical y horizontal en Distancia de ruta, Asignación de la distancia de ruta y Vínculo de menor distancia de ruta.
Las fórmulas descritas en las secciones anteriores reflejan cómo se realizan los cálculos con la dirección del viaje Viaje hasta el origen. Para la opción Viaje desde el origen, las fórmulas se invierten. Por ejemplo, si la parte de la fórmula relativa a la tasa de resistencia se aísla, la siguiente fórmula general se usa para las primeras cinco celdas cuando el viaje se produce en dirección contraria al origen:
Viaje desde el origen
a5 = c1 + c2 (1+r) + c3 (1+r)2 + c4(1+r)3 + c5(1+r)4- Donde
a5: menor coste acumulativo para las cinco primeras celdas
ci: identificador de celda
r: tasa de resistencia
El otro ajuste de este parámetro representa la inversa de la fórmula, como se ve a continuación:
Viaje hasta el origen
a5 = c1 (1+r)4 + c2 (1+r)3 + c3 (1+r)2 + c4 (1+r) + c5