Mínimos cuadrados ordinarios (OLS)—Ayuda

Resumen
Ilustración
Uso
Sintaxis
Muestra de código
Entornos
Información sobre licencias

Resumen

Realiza una regresión lineal global de Mínimos cuadrados ordinarios (OLS) para generar una predicción o modelar una variable dependiente en términos de sus relaciones con un conjunto de variables explicativas.

Puede acceder a los resultados de esta herramienta (incluido el archivo de informe opcional) desde la ventana Resultados. Si deshabilita el procesamiento en segundo plano, los resultados también se escriben en el cuadro de diálogo Progreso.

Más información sobre cómo funciona la regresión de Mínimos cuadrados ordinarios

Ilustración

Regresión de OLS — Regresión de mínimos cuadrados ordinarios: valores previstos con relación con valores observados

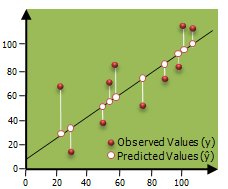
Uso

La principal salida para esta herramienta es un archivo de informe que se escribe en la ventana Resultados. Al hacer clic con el botón derecho del ratón en la entrada Mensajes de la ventana Resultados y seleccionar Ver, se muestra el informe de resumen Regresión exploratoria en un cuadro de diálogo Mensaje.
Nota:
Si esta herramienta es parte de una herramienta de modelo personalizado, las tablas opcionales solo aparecerán en la ventana Resultados si se configuran como parámetros de modelo antes de ejecutar la herramienta.
La herramienta OLS también produce una clase de entidad de salida y tablas opcionales con diagnósticos e información de coeficiente. Se puede acceder a todo esto en la ventana Resultados. La clase de entidad de salida se agrega automáticamente a la Tabla de contenido con un esquema de representación cálido/frío que se aplica a los residuales del modelo. En Interpretar los resultados de OLS se proporciona una explicación completa de cada salida.
Los resultados de la regresión OLS son confiables solo si los datos y el modelo de regresión satisfacen todas las presuposiciones que este método requiere inherentemente. Consulte la tabla Problemas, consecuencias y soluciones comunes de regresión en Conceptos básicos del análisis de regresión para asegurarse de que el modelo esté especificado correctamente.
Las variables dependientes y explicativas deben ser campos numéricos que contengan una variedad de valores. OLS no puede proporcionar soluciones cuando todas las variables tienen el mismo valor (por ejemplo, todos los valores de un campo son 9,0). Los métodos de regresión lineal, como OLS, no son adecuados para prever resultados binarios (por ejemplo, todos los valores para la variable dependiente son 1 o 0).
El campo de Id. único vincula las predicciones del modelo con cada entidad. Como consecuencia, los valores de Id. único deben ser únicos para cada entidad y, por lo general, deben ser un campo que se mantiene unido a la clase de entidad. Si no tiene un campo de Id. único, puede crear uno fácilmente al agregar un nuevo campo de entero a la tabla de clase de entidad y calcular los valores de campo para que sean iguales a los del campo FID/OID. No puede utilizar el campo FID/OID directamente para el parámetro Id. único.
Cuando haya una autocorrelación espacial estadísticamente significativa de los residuales de la regresión, se considerará que el modelo OLS está mal especificado y, por lo tanto, los resultados de la regresión OLS no serán confiables. Asegúrese de ejecutar la herramienta Autocorrelación espacial en los residuales de la regresión para evaluar este problema potencial. La autocorrelación espacial estadísticamente significativa de los residuales de regresión casi siempre indica la ausencia de una o más variables explicativas clave en el modelo.
Debe inspeccionar visualmente las sobrepredicciones y las subpredicciones que sean evidentes en los residuales de regresión para ver si proporcionan pistas acerca de las posibles variables que están ausentes en el modelo de regresión. Por lo general, esto ayuda a ejecutar el Análisis de punto caliente en los residuales para visualizar el clustering espacial de las sobrepredicciones y las subpredicciones.
Cuando se produce una especificación incorrecta como resultado del intento de modelar variables no estacionarias con un modelo global (OLS es un modelo global), se puede utilizar una Regresión ponderada geográficamente para mejorar las predicciones y comprender mejor la no estacionariedad (variación regional) inherente en las variables explicativas.
Cuando el resultado de un cálculo es infinito o indefinido, la salida para los no shapefiles será Nulo; para los shapefiles la salida será -DBL_MAX (-1,7976931348623158e+ 308, por ejemplo).
Los diagnósticos del resumen del modelo se escriben en el informe de resumen de OLS y la tabla de salida de diagnóstico opcional. Ambos incluyen diagnósticos para el Criterio de información de Akaike corregido (AICc), el Coeficiente de determinación, el índice estadístico F conjunto, el índice estadístico de Wald, el índice estadístico Breusch-Pagan de Koenker y el índice estadístico de Jarque-Bera. La tabla de diagnóstico también incluye valores AIC y Sigma cuadrado sin corregir.
Las tablas de salida de coeficiente o diagnóstico opcionales se sobrescribirán, si existen, cuando está activada la Opción de geoprocesamiento sobrescribir los resultados de las operaciones de geoprocesamiento.
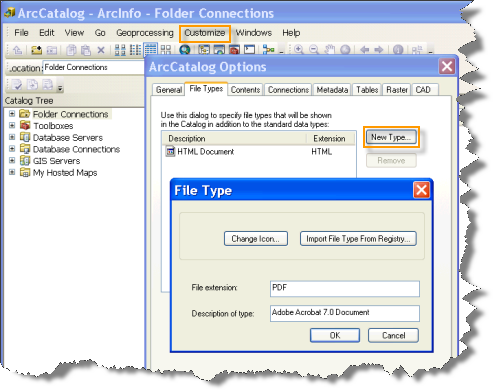
Esta herramienta creará opcionalmente un informe en PDF que resume los resultados. Los archivos PDF no aparecen automáticamente en la ventana Catálogo. Si desea que los archivos PDF se muestren en el Catálogo, abra la aplicación ArcCatalog, seleccione la opción de menú Personalizar, haga clic en Opciones de ArcCatalog y seleccione la pestaña Tipos de archivo. Haga clic en el botón Nuevo tipo y especifique PDF, según se muestra abajo, para Extensión de archivo.
En los equipos configurados con los paquetes de idiomas de ArcGIS para árabe y otros idiomas que se escriben de derecha a izquierda, es posible que observe que falta texto o que detecte problemas de formato en el PDF Archivo de informe de salida. Estos problemas se analizan en este artículo.
Las capas del mapa se pueden utilizar para definir la Clase de entidad de entrada. Cuando se utiliza una capa con una selección, solo las entidades seleccionadas se incluyen en el análisis.

Sintaxis

OrdinaryLeastSquares(Input_Feature_Class, Unique_ID_Field, Output_Feature_Class, Dependent_Variable, Explanatory_Variables, {Coefficient_Output_Table}, {Diagnostic_Output_Table}, {Output_Report_File})

Parámetro	Explicación	Tipo de datos
Input_Feature_Class	La clase de entidad que contiene las variables dependientes e independientes para el análisis.	Feature Layer
Unique_ID_Field	Un campo entero que contiene un valor diferente para cada entidad en la Clase de entidad de entrada.	Field
Output_Feature_Class	La clase de entidad de salida que recibirá estimaciones y residuales de variables dependientes.	Feature Class
Dependent_Variable	El campo numérico que contiene los valores de aquello que intenta modelar.	Field
Explanatory_Variables [Explanatory_Variables,...]	Una lista de campos que representan variables explicativas en el modelo de regresión.	Field
Coefficient_Output_Table (Opcional)	La ruta completa a una tabla opcional que recibirá los coeficientes del modelo, coeficientes estandarizados, los errores estándar y las probabilidades para cada variable explicativa.	Table
Diagnostic_Output_Table (Opcional)	La ruta completa a una tabla opcional que recibirá los diagnósticos del resumen del modelo.	Table
Output_Report_File (Opcional)	La ruta al archivo PDF opcional que desea que la herramienta cree. Este archivo de informe incluye diagnóstico del modelo, gráficos y notas para ayudarle a interpretar los resultados de OLS.	File

Muestra de código

Ejemplo 1 de OrdinaryLeastSquares (ventana de Python)

La siguiente secuencia de comandos de la ventana de Python muestra cómo utilizar la herramienta OrdinaryLeastSquares.

import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID","olsResults.shp", 
                                 "GROWTH","LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                                 "olsCoefTab.dbf","olsDiagTab.dbf")

Ejemplo 2 de OrdinaryLeastSquares (secuencia de comandos de Python independiente)

La siguiente secuencia de comandos de Python independiente muestra cómo utilizar la herramienta OrdinaryLeastSquares.

# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
    # Set the current workspace (to avoid having to specify the full path to the feature classes each time)
    arcpy.env.workspace = workspace
    # Growth as a function of {log of starting income, dummy for South
    # counties, interaction term for South counties, population density}
    # Process: Ordinary Least Squares... 
    ols = arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID", 
                        "olsResults.shp", "GROWTH",
                        "LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                        "olsCoefTab.dbf",
                        "olsDiagTab.dbf")
    # Create Spatial Weights Matrix (Can be based off input or output FC)
    # Process: Generate Spatial Weights Matrix... 
    swm = arcpy.GenerateSpatialWeightsMatrix_stats("USCounties.shp", "MYID",
                        "euclidean6Neighs.swm",
                        "K_NEAREST_NEIGHBORS",
                        "#", "#", "#", 6) 
                        
    # Calculate Moran's Index of Spatial Autocorrelation for 
    # OLS Residuals using a SWM File.  
    # Process: Spatial Autocorrelation (Morans I)...      
    moransI = arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual",
                        "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE", 
                        "EUCLIDEAN_DISTANCE", "NONE", "#", 
                        "euclidean6Neighs.swm")
except:
    # If an error occurred when running the tool, print out the error message.
    print(arcpy.GetMessages())

Entornos

Información sobre licencias

Basic: Sí
Standard: Sí
Advanced: Sí

ArcMap

Mínimos cuadrados ordinarios (OLS)