Descripción
La herramienta Transformar convierte los datos de un sistema de coordenadas a otro. Se suele utilizar para convertir coberturas creadas en unidades del digitalizador (habitualmente, pulgadas) en unidades del mundo real representadas en el manuscrito del mapa. Estas ubicaciones del mundo real se representan mediante una proyección en particular; por ejemplo, la proyección del mapa base puede ser UTM con ubicaciones de puntos de control medidas en metros.
Para realizar una transformación, debe poder registrar por lo menos dos puntos de relevancia de la cobertura en ubicaciones reales. Estas ubicaciones reales se pueden medir en pies o metros utilizando el sistema de coordenadas del mapa base, o se pueden encontrar en intersecciones de latitud-longitud. Si las ubicaciones hacen referencia a grados de latitud y longitud, utilice la herramienta Proyecto para convertir los puntos de control al sistema de coordenadas que corresponda al mapa base, medido en pies o metros. Haga esto antes de transformar la cobertura digitalizada.
Al transformar inicialmente los datos, estará transformándolos a la misma proyección del mapa de origen. A continuación, puede utilizar la herramienta Proyecto para convertir la cobertura a otra proyección cartográfica.
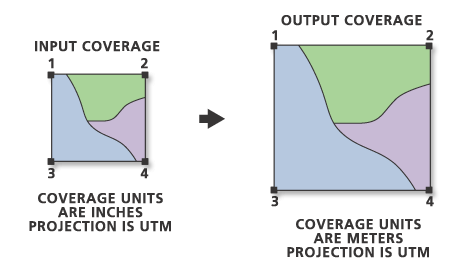
La herramienta Transformar se basa en la comparación de las coordenadas de los puntos de relevancia de la cobertura de entrada con los puntos de relevancia correspondientes de la cobertura de salida. Los ID de punto de relevancia identifican los puntos de relevancia que se van a comparar. El número mínimo de puntos de relevancia necesarios depende de qué opción de transformación se utilice. Los puntos de relevancia se tratan como puntos de control para la transformación y no se convierten con la ecuación de transformación. Las coordenadas de los puntos de relevancia de salida no cambiarán después de la transformación. Sin embargo, las entidades que coincidan con los puntos de relevancia de entrada no coincidirán normalmente con los puntos de relevancia de salida. Puede que necesite ajustar las entidades para forzarlas a coincidir con los puntos de relevancia de la cobertura de salida después de la transformación.
La herramienta Transformar, de forma predeterminada, utiliza una función de transformación AFFINE para transformar las coordenadas de la cobertura de entrada en la cobertura de salida. Se requiere un mínimo de tres puntos de relevancia para calcular una transformación afín.
Una transformación afín puede escalar los datos diferencialmente, sesgarlos, rotarlos y traducirlos. El siguiente gráfico ilustra los cuatro cambios posibles.
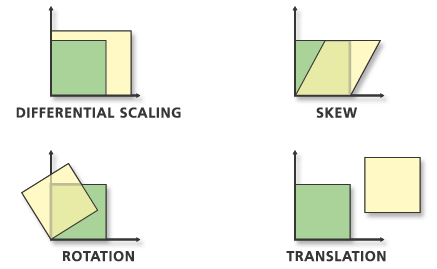
La función de transformación afín es:
x’ = Ax + By + CLos parámetros A-F los determinan los puntos de control
y’ = Dx + Ey + Fa continuación, se aplican a todas las coordenadas de la cobertura.
donde x e y son coordenadas de la cobertura de entrada, y x' e y' con coordenadas de la cobertura de salida. A, B, C, D, E y F se determinan comparando la ubicación de los puntos de relevancia de la cobertura de entrada y su ubicación en la cobertura de salida. Escalan, sesgan, rotan y traducen las coordenadas de los puntos de relevancia.
La herramienta Transformar comunica los seis parámetros y su interpretación geométrica. Éste es un ejemplo de parte del informe de salida para una transformación afín.
Transformar coordenadas para cobertura en in_cov_name
Scale (X,Y) = (246.140,255.702) Skew (degrees) = (-0.061) Rotation (degrees) = (0.334) Translation = (2890.267,3679.906) RMS Error (input, output) = (0.084,20.592) Affine X = Ax + By + C Y = Dx + Ey + F A = 246.135 B = -1.763 C = 2890.267 D = 1.434 E = 255.696 F = 3679.906
Una sección del informe muestra los parámetros de las ecuaciones de transformación. Puede interpretar los parámetros de la ecuación para entender lo que está pasando geométricamente. La primera sección del informe proporciona los valores interpretados del ajuste de escala, sesgo y rotación. Reorganizar el orden de la aplicación de estas acciones geométricas cambia los valores interpretados, pero el resultado final y los parámetros de la ecuación siempre son los mismos. El orden de interpretación utilizado es (1) escalar, (2) sesgar en la dirección x y (3) rotación en sentido contrario a las agujas del reloj de los puntos alrededor de los ejes. Los valores de traducción no se interpretan, sino que son simplemente los parámetros de traducción C y F de las ecuaciones. La herramienta Transformar interpreta los parámetros de la ecuación afín de la siguiente manera:
A = mx · cos t B = my · (k · cos t - sin t) D = mx · sin t E = my · (k · sin t + cos t) C = translation in x direction F = translation in y direction where mx = change of scale in x direction my = change of scale in y direction k = shear factor along the x-axis = tan (skew angle) (the skew angle is measured from the y-axis) t = rotation angle, measured counterclockwise from the x-axis
El ángulo de rotación hace referencia a la rotación de los datos alrededor de un sistema de coordenadas x,y fijo. Haciendo referencia a la figura anterior, los datos originales han rotado 45 grados. Un valor negativo significa que los datos rotan en el sentido de las agujas del reloj respecto al eje x.
La transformación SIMILARITY escala, rota y traduce los datos. No escalará los ejes independientemente ni introducirá ningún sesgo. Una transformación de similitud requiere un mínimo de dos puntos de control. Éste es el informe de una transformación de similitud utilizando las mismas coberturas previamente transformadas con una transformación afín.
Transformar coordenadas para cobertura en in_cov_name
Scale (X,Y) = (249.927,249.927) Rotation (degrees) = (0.362) Translation = (2855.407,3715.168) RMS Error (input, output) = (0.118,29.398) Similarity X = Ax + By + C Y = -Bx + Ay + F A = 249.922 B = -1.578 C = 2855.407 F = 3715.168
Observe que los valores de escala X e Y son iguales. No se comunica un valor de sesgo, porque la transformación de similitud no permite que se introduzca ningún movimiento no ortogonal en los datos.
La función de transformación de similitud es
x’ = Ax + By + C y’ = -Bx + Ay + F where A = s · cos t B = s · sin t C = translation in x direction F = translation in y direction and s = scale change (same in x and y directions) t = rotation angle, measured counterclockwise from the x-axis
Como ocurre en la explicación de AFFINE, el ángulo de rotación hace referencia a la rotación de los datos alrededor de un sistema de coordenadas x,y fijo. Haciendo referencia a la figura anterior, los datos originales han rotado 45 grados. Un valor negativo significa que los datos rotan en el sentido de las agujas del reloj respecto al eje x.
La transformación PROJECTIVE se basa en una fórmula más compleja que requiere un mínimo de cuatro puntos de relevancia.
x’ = (Ax + By + C) / (Gx + Hy + 1) y’ = (Dx + Ey + F) / (Gx + Hy + 1)El informe PROJECTIVE incluye la escala aproximada, el error RMS y los parámetros de la ecuación. Debido a la complejidad de la interpretación, los parámetros de la transformación descriptiva no se interpretan. Para obtener más información, consulte uno de los textos sobre fotogrametría que aparecen en las referencias al final de este tema. A continuación aparece un ejemplo de informe de salida para una transformación descriptiva.
Transformar coordenadas para cobertura en in_cov_name
Approximate scale = 1479.087 RMS Error (input, output) = (0.040,60.878) 2D Projective X = (Ax + By + C) / (Gx + Hy + 1) Y = (Dx + Ey + F) / (Gx + Hy + 1) A = 55.667 B = -718.999 C = 2125052.558 D = -199.525 E = 1385.541 F = 317759.475 G = -0.001 H = 0.000 Principal point of input (xp,yp) = (2.000,16.946) Exposure center of output(Xc,Yc) = (2127791.000,343183.000)
El punto principal y el centro de la exposición corresponden al primer punto de relevancia en el archivo de puntos de relevancia de la cobertura de entrada. Si desea utilizar otro punto (por ejemplo, el centro del dataset), asegúrese de que sea el primer punto de relevancia del archivo.
Para cada transformación realizada se calcula un error cuadrático medio (RMS), que indica la calidad de la transformación derivada. En el siguiente ejemplo se muestra la ubicación relativa de cuatro puntos de control de salida (puntos de relevancia) y los puntos de control de entrada transformados:
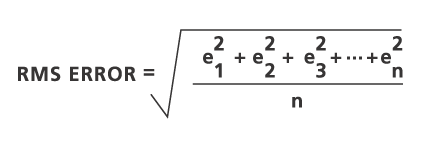
El error RMS mide los errores entre los puntos de relevancia de la cobertura de salida y las ubicaciones transformadas de los puntos de relevancia de la cobertura de entrada.
La transformación se deriva utilizando mínimos cuadrados, así que se puede proporcionar más puntos de relevancia que los necesarios.
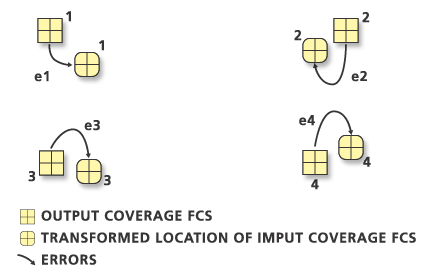
El error RMS para cada transformación se indica tanto en unidades de la cobertura de entrada (por ejemplo, 0,031 pulgadas) como en unidades de la cobertura de salida (por ejemplo, 37,465 pies).
RMS Error (input, output) = (0.031,37.465)Una transformación perfecta produce un error RMS de cero. Aunque no obtendrá ningún valor de 0,000, debe intentar mantener el error RMS tan bajo como sea posible. Es mejor establecer y mantener un error máximo aceptable. Los valores aceptables variarán en función de la precisión de los datos originales y de la escala del mapa de origen. Los errores RMS altos indican que los puntos de relevancia anteriores y los puntos de relevancia nuevos no corresponden a las mismas ubicaciones relativas. Si el error RMS es más alto que el valor establecido, puede indicar problemas de conversión que pueden extender la cobertura de salida incorrectamente.
La última parte del informe muestra las coordenadas de los puntos de relevancia de entrada y salida, y sus errores x e y (vea a continuación). Los parámetros de transformación son el mejor ajuste entre los puntos de relevancia de entrada y salida. Si utiliza los parámetros de transformación para transformar los puntos de relevancia de entrada reales, las ubicaciones de salida transformadas no coincidirán con las ubicaciones verdaderas de los puntos de relevancia de salida. Los errores de x e y son una medida del ajuste entre las ubicaciones verdaderas y las ubicaciones transformadas de los puntos de relevancia de salida. A veces, se puede detectar un error examinando los errores de x e y.
tic id input x input y output x output y x error y error ------------------------------------------------------------------------ 1 2.000 16.946 2127791.000 343183.000 14.463 75.499 2 12.764 16.821 2143469.000 343326.000 -31.043 -85.363 3 2.052 1.976 2128000.000 320680.000 -36.290 -2.353 4 12.922 2.013 2143729.000 320912.000 20.245 -6.163 5 2.082 9.442 2127944.000 332015.000 22.016 -74.699 6 12.662 9.442 2143320.000 332015.000 10.609 93.079
Ejemplo
En este ejemplo se transforma una cobertura de las unidades del digitalizador a coordenadas del mundo real. La cobertura original denominada INCHCOV tiene los siguientes puntos de control medidos en pulgadas del digitalizador:
IDTIC XTIC YTIC 1 2.000 16.946 2 12.764 16.821 3 2.052 1.976 4 12.922 2.013 5 2.082 9.442 6 12.662 9.442
El mapa base utilizado estaba en el sistema de coordenadas del plano de estado con puntos de control medidos en pies. Cada punto de relevancia corresponde a las siguientes ubicaciones:
Tic-IDs X Coordinates Y Coordinates 1 2,127,791 343,183 2 2,143,469 343,326 3 2,128,000 320,680 4 2,143,729 320,912 5 2,127,944 332,015 6 2,143,320 332,015
La cobertura de salida debe existir antes de ejecutar la herramienta Transformar. Utilice la herramienta Crear cobertura para crear la cobertura de salida y copie los archivos TIC y BND de la cobertura de entrada, si lo desea. Opcionalmente, puede utilizar la herramienta Generar para crear una nueva cobertura que contenga puntos de relevancia en las ubicaciones deseadas.
El archivo de puntos de relevancia para la cobertura de salida debe contener coordenadas x,y para cada punto de relevancia que se vaya a conservar en la cobertura de salida; en este caso, las ubicaciones de los puntos de relevancia del sistema de coordenadas del plano de estado. Las coordenadas de los puntos de relevancia se pueden ajustar en ArcMap o en los módulos TABLES o INFO de ArcInfo Workstation.
Una vez creados los nuevos puntos de relevancia, las entidades de la cobertura digitalizada se pueden transformar en unidades del mundo real. La herramienta Transformar se utiliza para convertir una cobertura de proyección del plano de estado a la que se haga referencia en pulgadas (INCHCOV) en una cobertura de proyección del plano de estado a la que se haga referencia en pies (STATECOV). Éste es un ejemplo de la transformación AFFINE.
Scale (X,Y) = (1452.317,1508.433) Skew (degrees) = (0.416) Rotation (degrees) = (0.218) Translation = (2124994.654,317664.385) RMS Error (input, output) = (0.048,71.614) Affine X = Ax + By + C Y = Dx + Ey + F A = 1452.230 B = -5.526 C = 2124994.654 D = 15.858 E = 1508.462 F = 317664.385 tic id input x input y output x output y x error y error -------------------------------------------------- 1 2.000 16.946 2127791.000 343183.000 14.463 75.499 2 12.764 16.821 2143469.000 343326.000 -31.043 -85.363 3 2.052 1.976 2128000.000 320680.000 -36.290 -2.353 4 12.922 2.013 2143729.000 320912.000 20.245 -6.163 5 2.082 9.442 2127944.000 332015.000 22.016 -74.699 6 12.662 9.442 2143320.000 332015.000 10.609 93.079
Éste es el ejemplo correspondiente de una transformación PROJECTIVE para la misma cobertura. Recuerde que la opción PROJECTIVE solo se utiliza normalmente cuando las coberturas originales se digitalizan directamente a partir de fotos aéreas.
Transformar coordenadas para INCHCOV de cobertura
Approximate scale = 1479.087 RMS Error (input, output) = (0.040,60.878) 2D Projective X = (Ax + By + C) / (Gx + Hy + 1) Y = (Dx + Ey + F) / (Gx + Hy + 1) A = 55.667 B = -718.999 C = 2125052.558 D = -199.525 E = 1385.541 F = 317759.475 G = -0.001 H = 0.000 Principal point of input (xp,yp) = (2.000,16.946) Exposure center of output(Xc,Yc) = (2127791.000,343183.000) tic id input x input y output x output y x error y error -------------------------------------------------- 1 2.000 16.946 2127791.000 343183.000 -4.438 45.252 2 12.764 16.821 2143469.000 343326.000 -11.447 -36.202 3 2.052 1.976 2128000.000 320680.000 -17.300 46.421 4 12.922 2.013 2143729.000 320912.000 1.704 -36.962 5 2.082 9.442 2127944.000 332015.000 21.787 -93.410 6 12.662 9.442 2143320.000 332015.000 9.694 74.901
Finalmente, ésta es la misma cobertura transformada utilizando la opción SIMILARITY.
Transformar coordenadas para cobertura en inchcov
Scale (X,Y) = (1483.794,1483.794) Rotation (degrees) = (0.377) Translation = (2124800.900,317942.729) RMS Error (input,output) = (0.162,240.958) Similarity X = Ax + By + C Y = -Bx + Ay + F A = 1483.762 B = -9.765 C = 2124800.900 F = 317942.729 tic id input x input y output x output y x error y error -------------------------------------------------- 1 2.000 16.946 2127791.000 343183.000 -188.053 -76.916 2 12.764 16.821 2143469.000 343326.000 106.378 -300.277 3 2.052 1.976 2128000.000 320680.000 -173.717 214.680 4 12.922 2.013 2143729.000 320912.000 225.411 143.724 5 2.082 9.442 2127944.000 332015.000 -146.109 -42.262 6 12.662 9.442 2143320.000 332015.000 176.089 61.051
En el siguiente ejemplo se invierte una cobertura mediante una transformación AFFINE.
Transformar coordenadas para marcador de cobertura
Scale (X,Y) = (1.000,-1.000) Skew (degrees) = (0.000) *** Negative Y scaling indicates reflection around X axis. *** Rotation (degrees) = (180.000) Translation = (800.000,0.000) RMS Error (input, output) = (0.000,0.000) Affine X = Ax + By + C Y = Dx + Ey + F A = -1.000 B = 0.000 C = 800.000 D = 0.000 E = 1.000 F = 0.000 tic id input x input y output x output y x error y error -------------------------------------------------- 1 700.000 100.000 100.000 100.000 0.000 0.000 2 700.000 800.000 100.000 800.000 0.000 0.000 3 100.000 800.000 700.000 800.000 0.000 0.000 4 100.000 100.000 700.000 100.000 0.000 0.000
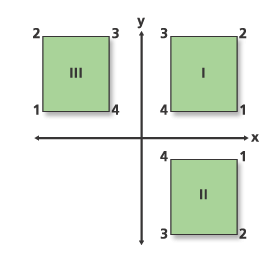
Observe el mensaje del informe de salida sobre la reflexión. Lo que le ocurre a la cobertura se muestra en el gráfico siguiente. El rectángulo etiquetado I es la cobertura de entrada. Se aplica una escala Y de -1 a las coordenadas. Esto produce el rectángulo II. No hay ningún factor de sesgo, de modo que los puntos rotan 180 grados, lo que lo coloca en la posición III. El paso final (no se muestra) es traducir la cobertura.
Referencias
Maling, D.H., Coordinate Systems and Map Projections. George Philip., 1973.
Maling, D. H ., “Sistemas de coordenadas y proyecciones cartográficas para SIG”. Entrada: Maguire, D.J., M.F. Goodchild y D.W. Rhind (eds.), Sistemas de información geográfica: principios y aplicaciones. Vol. 1, pág. 135-146. Longman Group UK Ltd., 1991.
Moffitt, F. H. y E. M. Mikhail, fotogrametría. Third Edition. Harper and Row, Inc., 1980.
Pettofrezzo, A.J., Matrices and Transformations. Dover Publications, Inc., 1966.
Slama, C.C., C. Theurer, and S.W. Henriksen (eds.), Manual of Photogrammetry. 4ta. edición. Capítulo XIV, pág. 729-731. ASPRS, 1980.