Disponible con una licencia de Spatial Analyst.
La herramienta Estadísticas de conjunto de bandas proporciona las estadísticas para el análisis multivariado de un conjunto de bandas de ráster. Cuando está activado el uso de la opción Calcular matrices de covarianza y correlación, las matrices de covarianza y correlación generan salidas así como los parámetros estadísticos básicos, tales como los valores de la desviación mínima, máxima, media y estándar para cada capa.
La matriz de covarianza contiene valores de varianzas y covarianzas. La varianza es una medida estadística que muestra cuánta varianza hay desde la media. Para calcular estas varianzas, se promedian los cuadrados de las diferencias entre cada valor de celda y el valor medio de todas las celdas. Las varianzas para cada capa se pueden leer a lo largo de la diagonal de la matriz de covarianza desde la parte superior izquierda hasta la inferior derecha. Las varianzas se expresan en unidades de valor de celda al cuadrado.
Las entradas restantes dentro de la matriz de covarianza son las covarianzas entre todos los pares de rásteres de entrada. La siguiente fórmula se utiliza para determinar la covarianza entre las capas i y j:
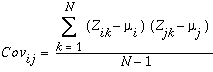
donde:
Z - valor de una celda
i, j - son las capas de una pila
µ - es la media de una capa
N: es la cantidad de celdas
k - denota una determinada celda
La covarianza de dos capas es la intersección de la fila y la columna apropiadas. La covarianza entre las capas 2 y 3 es la misma que la covarianza entre las capas 3 y 2. Los valores de la matriz de covarianza dependen de las unidades de valor, mientras que los valores de la matriz de correlación no.
La matriz de correlación muestra los valores de los coeficientes de correlación que representan la relación entre los dos datasets. En el caso de un conjunto de capas ráster, la matriz de correlación presenta los valores de celda de una capa ráster a medida que se relacionan con los valores de celda de otra capa. La correlación entre las dos capas es una medida de dependencia entre las capas. Es la relación de la covarianza entre las dos capas dividido por el producto de sus desviaciones estándares. Debido a que es una relación, es un número sin unidades. La ecuación para calcular la correlación es la siguiente:
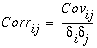
La correlación varía de +1 a -1 grados. Una correlación positiva indica una relación directa entre dos capas; así, cuando los valores de celda de una capa aumentan, es probable que los valores de celda de otra capa también aumenten. Una correlación negativa significa que una variable cambia de manera inversa a la otra. Una correlación de cero significa que las dos capas son independientes entre sí.
La matriz de correlación es simétrica. La diagonal desde la parte superior izquierda a la inferior derecha es 1,0000 debido a que el coeficiente de correlación de capas idénticas es +1.
Ejemplo
El siguiente ejemplo muestra los contenidos de las salida desde Estadísticas de conjunto de bandas para un ráster multibanda de cuatro capas. La primera tabla muestra las estadísticas básicas cuando no se utiliza la opción Calcular matrices. Sin embargo, cuando se marca la opción, también se calculan las matrices de covarianza y correlación. Se muestran las estadísticas de salida que contiene el archivo de estadísticas de salida.
Sólo se calculó la media
Salida con Calcular matrices de covarianza y correlación deshabilitada (BRIEF):
# STATISTICS of INDIVIDUAL LAYERS
# Layer MIN MAX MEAN STD
# ---------------------------------------------------------------
1 1.0000 21.0000 7.8410 4.1690
2 1.0000 128.0000 25.5144 35.8494
3 296.9573 4073.6306 1565.5359 763.9803
4 0.3333 127.5000 51.5314 29.7958
# ===============================================================Se calculó tanto la media como las matrices
Salida con Calcular matrices de covarianza y correlación habilitada (DETAILED):
# STATISTICS of INDIVIDUAL LAYERS
# Layer MIN MAX MEAN STD
# ---------------------------------------------------------------
1 1.0000 21.0000 7.8410 4.1690
2 1.0000 128.0000 25.5144 35.8494
3 296.9573 4073.6306 1565.5359 763.9803
4 0.3333 127.5000 51.5314 29.7958
# ===============================================================
# COVARIANCE MATRIX
# Layer 1 2 3 4
# ---------------------------------------------------------------
1 17.3826 16.9320 3177.5947 87.9590
2 16.9320 1285.3096 3117.1753 31.3420
3 3177.5947 3117.1753 583723.0625 16137.9785
4 87.9590 31.3420 16137.9785 887.8751
# ===============================================================
# CORRELATION MATRIX
# Layer 1 2 3 4
# ---------------------------------------------------------------
1 1.0000 0.1133 0.9976 0.7080
2 0.1133 1.0000 0.1138 0.0293
3 0.9976 0.1138 1.0000 0.7089
4 0.7080 0.0293 0.7089 1.0000
# ===============================================================Referencias
Snedecor, G. W. y W. G. Cochran. 1968. Statistical Methods, 6ª ed. The Iowa State University Press: Ames, Iowa.