Disponible avec une licence Spatial Analyst.
L'interpolation de pondération par l'inverse de la distance (IDW) détermine les valeurs de cellule via la combinaison pondérée de manière linéaire d'un ensemble de points d'échantillonnage. La pondération est une fonction d'inverse de la distance. La surface qui est interpolée doit être celle d'une variable dépendante de l'emplacement.
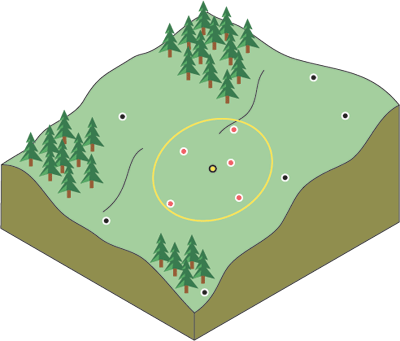
Cette méthode suppose que l'influence de la variable tracée décroît avec la distance par rapport à l'emplacement échantillonné. Par exemple, lors de l'interpolation de la surface du pouvoir d'achat des consommateurs pour l'analyse d'un site de détaillants, le pouvoir d'achat d'un emplacement plus lointain aura moins d'influence car les gens ont tendance à effectuer leurs achats à côté de chez eux.
Contrôle de l'influence avec le paramètre Puissance
L'IDW repose principalement sur l'inverse de la distance élevée à une puissance mathématique. Avec le paramètre Puissance, vous pouvez contrôler la signification des points connus sur les valeurs interpolées en fonction de leur distance par rapport au point en sortie. Il s'agit d'un nombre positif et réel dont la valeur par défaut est 2.
La définition d'une puissance plus élevée permet une concentration sur les points les plus proches. Ainsi, les données proches auront plus d'influence et la surface comportera davantage de détails (sera moins lisse). Lorsque la puissance augmente, les valeurs interpolées commencent à approcher la valeur du point d'échantillonnage le plus proche. Une valeur de puissance moins élevée accorde plus d'influence aux points environnants les plus éloignés, ce qui génère une surface plus lisse.
Puisque la formule IDW n'est pas liée à un processus physique réel, il n'y a aucun moyen de savoir si une valeur de puissance particulière est trop élevée. D'une manière générale, une puissance de 30 est considérée comme extrêmement élevée et est donc à utiliser avec prudence. N'oubliez pas également qui si les distances sont grandes ou si la valeur de puissance est élevée, les résultats peuvent être incorrects.
On considère qu'une valeur de puissance est optimale lorsque l'erreur absolue moyenne minimale est la plus basse. L'Extension ArcGIS Geostatistical Analyst permet d'étudier ceci.
Limitation des points utilisés pour l'interpolation
Il est aussi possible de contrôler les caractéristiques de la surface interpolée en limitant le nombre de points en entrée utilisés dans le calcul de la valeur de chaque cellule en sortie. Cette limitation peut augmenter les vitesses de traitement. N'oubliez pas également que les points en entrée qui sont éloignés de l'emplacement de cellule où la prévision est réalisée peuvent bénéficier d'une corrélation spatiale faible ou inexistence. Il peut donc être utile de les éliminer du calcul.
Vous pouvez spécifier le nombre de points à utiliser directement ou indiquer un rayon constant dans lequel les points seront inclus dans l'interpolation.
Rayon de recherche variable
Avec un rayon de recherche variable, le nombre de points utilisé dans le calcul de la valeur de la cellule interpolée est spécifié. Le rayon varie donc pour chaque cellule interpolée en fonction du champ de recherche nécessaire pour trouver le nombre spécifié de points en entrée. Ainsi, certains voisinages sont petits et d'autres plus grands en fonction de la densité des points mesurés à proximité de la cellule interpolée. Vous pouvez également spécifier une distance maximale (en unités de carte) que le rayon de recherche ne doit pas excéder. Si le rayon d'un voisinage particulier atteint la distance maximale avant d'obtenir le nombre de points spécifiés, la prévision de cet emplacement s'effectue sur la base du nombre de points mesurés se trouvant dans les limites de la même distance maximale. En principe, il convient d'utiliser des voisinages ou un nombre minimum de points plus petits lorsque le phénomène est sujet à une variation très importante.
Rayon de recherche constant
Un rayon de recherche constant nécessite la définition d'une distance par rapport au voisinage et d'un nombre minimum de points. La distance dicte le rayon du cercle de voisinage (en unités de carte). La distance du rayon étant constante, le rayon du cercle utilisé dans la recherche des points en entrée est le même pour chaque cellule interpolée. Le nombre minimal de points indique le minimum de points mesurés à utiliser dans le voisinage. Tous les points mesurés compris dans le rayon seront utilisés dans le calcul de chaque cellule interpolée. Lorsque le nombre de points mesurés dans un voisinage est inférieur au minimum spécifié, le rayon de recherche s'agrandit afin d'englober le minimum requis. Le rayon de recherche constant spécifié sera utilisé pour chaque cellule interpolée (centre de la cellule) de la zone d'étude. Par conséquent, si les points mesurés ne sont pas répartis de façon équilibrée (il ne le sont que très rarement), le nombre de points mesurés utilisé dans les prévisions sera probablement différent en fonction du voisinage.
Utilisation d'interruptions
Une interruption est un jeu de données polylignes utilisé comme ligne de fracture qui limite la recherche de points d'échantillonnage en entrée. Une polyligne qui représente une falaise, une crête ou toute autre interruption du paysage. Seuls les points d'échantillonnage en entrée se trouvant du même côté de l'interruption que la cellule en cours de traitement en cours seront pris en compte.
Bibliographie
Philip, G. M. et D. F. Watson. "A Precise Method for Determining Contoured Surfaces." Australian Petroleum Exploration Association Journal 22: 205–212. 1982.
Watson, D. F. et G. M. Philip. "A Refinement of Inverse Distance Weighted Interpolation." Geoprocessing 2:315–327. 1985.