Disponible avec une licence Spatial Analyst.
L'outil Spline utilise une méthode d'interpolation selon laquelle les valeurs sont déterminées à l'aide d'une fonction mathématique qui réduit la courbure globale des surfaces et restitue une surface lisse passant exactement par les points en entrée.
Arrière-plan conceptuel
En théorie, les points d'échantillonnage sont extrudés à la hauteur de leur magnitude. La spline courbe une feuille caoutchoutée qui passe par les points en entrée tout en réduisant la courbure totale de la surface. Elle applique une fonction mathématique à un nombre donné de points en entrée les plus proches tout en passant par les points d'échantillonnage. Cette méthode est parfaitement adaptée à la création de surfaces variant graduellement, telles que les altitudes, la profondeur des nappes phréatiques et les concentrations de pollution.
Le formulaire de base de l'interpolation par spline de courbure minimale impose les deux conditions suivantes à l'élément interpolé :
- La surface doit traverser exactement les points de données.
- La surface doit présenter une courbure minimale. La somme cumulée des carrés des termes de deuxième dérivée de la surface prise sur chaque point de la surface doit être un minimum.
La technique de courbure minimale de base est également appelée interpolation de plaque fine. Elle garantit une surface lisse (continue et distinguable) et des surfaces de première dérivée continues. Des changements rapides apportés au dégradé ou à la pente (première dérivée) peuvent survenir dans les environs des points de données. Ainsi, ce modèle n'est pas adapté à l'estimation de la deuxième dérivée (courbure).
La technique d'interpolation de base peut être appliquée en utilisant la valeur zéro pour l'argument Poids de l'outil Spline.
Types de spline
Il existe deux types de spline : Régularisé et Tension. Le type Régularisé crée une surface lisse à évolution progressive, avec des valeurs pouvant se trouver hors de plage de données d'échantillonnage. Le type Tension définit la tension de la surface en fonction du caractère du phénomène modélisé. Elle crée une surface lisse dont les valeurs sont plus étroitement restreintes par la plage de données d'échantillonnage.
Type de spline Régularisé
L'option REGULARIZED modifie les critères de minimisation pour que les termes de troisième dérivée soient incorporés aux critères de minimisation. Le paramètre Poids spécifie le poids associé aux termes de troisième dérivée pendant la minimisation, également nommé τ (tau) dans les ouvrages de référence. Les valeurs les plus élevées de ce terme génèrent des surfaces plus lisses. Des valeurs comprises entre 0 et 0,5 sont conseillées. Cette option garantit une surface lisse avec des surfaces lisses de première dérivée. Cette technique est utile si la deuxième dérivée de la surface interpolée doit être calculée.
Type de spline Tension
L'option TENSION modifie les critères de minimisation pour que les termes de première dérivée soient incorporés aux critères de minimisation. Le paramètre Poids spécifie le poids associé aux termes de première dérivée pendant la minimisation, également nommé Φ (phi) dans les ouvrages de référence. Un poids de résultats nuls est spécifié dans l'interpolation par spline de plaque fine de base. L'utilisation d'une valeur de poids plus élevée réduit la tension de la plaque, et dans la limite d'approche de l'infinie par phi, la surface s'apparente à la forme d'une membrane ou des feuilles de caoutchouc, traversant les points. La surface interpolée est lisse. Les premières dérivées sont continues mais ne sont pas lisses.
Paramètres de spline supplémentaires
Pour mieux contrôler les aspects de la surface en sortie, vous pouvez recourir à deux paramètres supplémentaires : le poids et le nombre de points.
Paramètre de poids
Pour la méthode de spline Régularisé, le paramètre Poids définit le poids de la troisième dérivée de la surface dans l'expression de réduction de la courbure. Plus le poids est élevé, plus la surface en sortie est lisse. Ce paramètre doit prendre des valeurs égales ou supérieures à zéro. Voici quelques valeurs standard : 0, 0,001, 0,01, 0,1 et 0,5.
Pour la méthode de spline Tension, le paramètre Poids définit le poids de la tension. Plus le poids est élevé, plus la surface en sortie est grossière. Les valeurs entrées doivent être égales ou supérieures à zéro. Voici quelques valeurs typiques : 0, 1, 5, 10.
Paramètre de nombre de points
Le Nombre de points identifie le nombre de points utilisés dans le calcul de chaque cellule interpolée. Plus vous définissez de points en entrée, plus les cellules sont influencées par les points éloignés et plus la surface en sortie est lisse. Plus le nombre de points est important, plus le traitement du raster en sortie est long.
Equation de spline
L'algorithme utilisé pour l'outil Spline applique la formule suivante pour l'interpolation de surface :
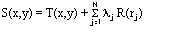
- où :
j = 1, 2, ..., N.
N est le nombre de points.
λj sont les coefficients trouvés par la solution d'un système d'équations linéaires.
rj est la distance du point (x, y) au point jth.
T(x,y) et R(r) sont définis différemment, selon l'option sélectionnée.
A des fins de calcul, tout l'espace du raster en sortie est divisé en blocs ou régions de même taille. Le nombre de régions est identique dans les directions x et y. Elles ont une forme rectangulaire. Le nombre de régions est déterminé en divisant le montant total de points dans le jeu de données ponctuelles en entrée par la valeur spécifiée pour le nombre de points. Pour les données distribuées avec moins d'uniformité, les régions peuvent contenir un nombre de points très différent, la valeur du nombre de points constituant seulement une moyenne approximative. Si dans une région, le nombre de points est inférieur à huit, la région sera développée jusqu'à ce qu'elle contienne un minimum de huit points.
Pour l'option Régularisé
T(x,y) = a1 + a2x + a3y- où :
ai sont les coefficients trouvés par la solution d'un système d'équations linéaires.
et
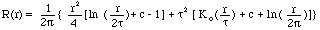
- où :
r est la distance entre le point et l'exemple.
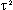est le paramètre Poids.Ko est la fonction de Bessel modifiée.
c est une constante égale à 0,577215.
Pour l'option Tension
T(x,y) = a1- où :
a1 est un coefficient trouvé par la solution d'un système d'équations linéaires.
et
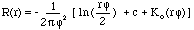
- où :
r est la distance entre le point et l'exemple.
φ2 est le paramètre Poids.
Ko est la fonction de Bessel modifiée.
c est une constante égale à 0,577215.
Traitement régional de sortie
A des fins de calcul, tout l'espace du raster en sortie est divisé en blocs ou régions de même taille. Le nombre de régions est identique dans les directions x et y. Elles ont une forme rectangulaire. Le nombre de régions est déterminé en divisant le montant total de points dans le jeu de données ponctuelles en entrée par la valeur spécifiée pour le nombre de points. Pour les données distribuées avec moins d'uniformité, les régions peuvent contenir un nombre de points très différent, la valeur du nombre de points constituant seulement une moyenne approximative. Si dans une région, le nombre de points est inférieur à huit, la région est développée jusqu'à ce qu'elle contienne un minimum de huit points.
Bibliographie
Franke, R. 1982. Smooth Interpolation of Scattered Data by Local Thin Plate Splines. Computer and Mathematics with Applications. Vol. 8. No. 4. pp. 273–281. Grande-Bretagne.
Mitas, L. et H. Mitasova. 1988. General Variational Approach to the Interpolation Problem. Computer and Mathematics with Applications. Vol. 16. No. 12. pp. 983–992. Grande-Bretagne.