L'interpolation par noyau est une variante d'une interpolation polynomiale locale de premier ordre dans laquelle l'instabilité des calculs est empêchée grâce à une méthode similaire à celle utilisée dans la régression de crête pour estimer les coefficients de régression. Lorsque l'estimation ne présente qu'une légère déformation et qu'elle est beaucoup plus précise qu'un outil d'estimation non déformé, elle peut tout à fait être privilégiée. Pour en savoir plus sur la régression de crête, vous pouvez par exemple consulter Hoerl et Kennard (1970).
L'erreur de prévision de l'interpolation polynomiale locale est estimée en supposant que le modèle est correct, c'est-à-dire que le numéro de condition spatiale est partout très petit. Cette supposition est souvent non respectée et le numéro de condition spatiale met en surbrillance les zones où les prévisions et les erreurs de prévision standard sont instables. Dans le modèle de lissage par noyau, le problème que posent les erreurs de prévision standard trop importantes et les prévisions douteuses est corrigé avec le paramètre de crête en introduisant un petit nombre de déformations dans les équations. Cela rend la carte du numéro de condition spatiale inutile. Par conséquent, l'interpolation par noyau offre uniquement une prévision et une erreur de prévision standard pour le type de surface en sortie. Comme le paramètre de crête introduit une déformation afin de stabiliser les prévisions, il doit être aussi petit que possible tout en préservant la stabilité du modèle. Ce processus est expliqué de manière détaillée dans l'ouvrage "Local Polynomials for Data Detrending and Interpolation in the Presence of Barriers", de Gribov et Krivoruchko (2010).
Autre différence entre les deux modèles : le modèle d'interpolation par noyau utilise la distance la plus courte entre les points de sorte que les points situés sur les côtés de l'interruption non transparente (absolue) spécifiée sont connectés par une série de lignes droites.
L'interpolation par noyau utilise les noyaux radialement symétriques suivants : Exponentiel, Gaussien, Quartique, Epanechnikov, Polynomial d'ordre 5 et Constant. La bande passante du noyau est déterminée par un rectangle autour des observations.
Le noyau Epanechnikov produit généralement de meilleurs résultats lorsque les transformations polynomiales de premier ordre sont utilisées. Toutefois, selon les données, les statistiques de validation croisée et de validation peuvent suggérer un autre noyau, de Fan et Gijbels (1996).
Les prévisions Interpolation par noyau avec interruptions absolues (à gauche) et sans (à droite) sont comparées ci-dessous. Notez comme les isolignes changeent brusquement aux interruptions dans le graphique de gauche, mais comme elles traversent doucement les interruptions dans le graphique de droite.
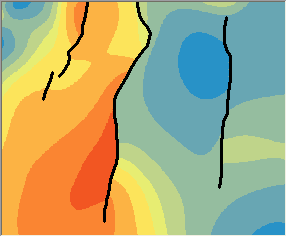
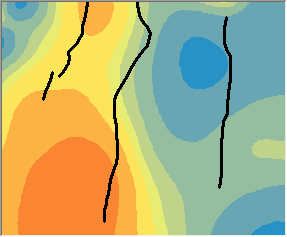
Les modèles reposant sur la distance la plus courte entre les points peuvent être préférables dans les applications hydrologiques et météorologiques.
Fonctions de noyau
Fonctions de noyau : pour toutes les formules ci-dessous, r est un rayon centré au point s et h est la bande passante.
- Exponentiel :
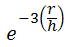
- Gaussien :
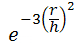
- Quartique :
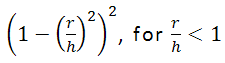
- Epanechnikov :
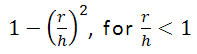
- PolynomialOrder5 :
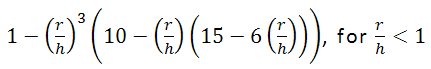
- Constant :
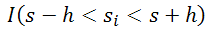
où I(expression) est une fonction d'indicateur qui accepte la valeur 1 si expression est True et la valeur 0 si expression est False.
Le paramètre de bande passante s'applique à toutes les fonctions de noyau, à l'exception de Constant. Les fonctions de noyau Exponentiel, Gaussien et Constant prennent également en charge un voisinage de recherche lissé afin de limiter la plage du noyau.
Références et lectures complémentaires
Fan, J. and Gijbels, I. (1996). Local Polynomial Modelling and Its Applications, Chapman & Hall. London.
Hoerl, A.E. and Kennard, R.W. (1970), Ridge regression: biased estimation for nonorthogonal problems, Technometrics, 12, 55-67.
Yan, Xin. (2009) Linear regression analysis : theory and computing. Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224.