Disponible avec une licence Geostatistical Analyst.
Le semi-variogramme illustre l'auto-corrélation spatiale des points d'échantillonnage mesurés. Lorsque chaque paire d'emplacements a été tracée (Binning du semi-variogramme empirique), un modèle est ajusté à travers ces derniers (Adapter un modèle au semi-variogramme empirique). Certaines caractéristiques sont souvent utilisées pour décrire ces modèles.
Plage et seuil
En observant un modèle de semi-variogramme, vous remarquez qu'à une certaine distance le modèle se stabilise. La distance à laquelle le modèle commence à s'aplanir est appelée la plage. Les emplacements d'échantillons séparés par une distance inférieure à la portée sont auto-corrélés spatialement alors que les emplacements séparés par une distance supérieure à la portée ne le sont pas.
La valeur que le semi-variogramme atteint à la plage (la valeur de l'axe des y) est appelée le seuil. Le seuil partiel correspond au seuil moins la pépite.
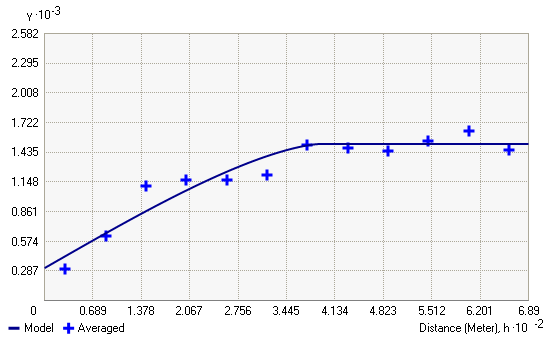
Pépite
Théoriquement, à une distance de séparation nulle (par exemple, décalage = 0), la valeur de semi-variogramme est 0. Toutefois, à une distance de séparation infiniment petite, le semi-variogramme présente souvent un effet de nugget, qui représente une valeur supérieure à 0. Par exemple, si le modèle de semi-variogramme intercepte l'axe des y à la valeur 2, la pépite prend alors la valeur 2.
L'effet de pépite peut être attribué à des erreurs de mesure ou à des sources de variation spatiale à des distances inférieures à l'intervalle d'échantillonnage, ou aux deux. Une erreur de mesure est le résultat d'une erreur inhérente à l'appareil de mesure. Les phénomènes naturels peuvent varier, dans l'espace, à des échelles diverses. Les variations à de petites échelles inférieures à la distance d'échantillonnage apparaîtront dans le cadre de l'effet pépite. Avant de collecter des données, il est important de bien comprendre les échelles de variation spatiale.