Moindres carrés ordinaires—Aide

Résumé
Illustration
Utilisation
Syntaxe
Exemple de code
Environnements
Informations de licence

Résumé

Exécute une régression linéaire globale à l'aide des moindres carrés ordinaires pour générer des prévisions ou modéliser une variable dépendante en fonction de ses relations à un ensemble de variables explicatives.

Vous pouvez accéder aux résultats de cet outil (fichier facultatif du rapport compris) par l'intermédiaire de la fenêtre Résultats. Si vous désactivez le traitement en arrière-plan, les résultats apparaissent également dans la boîte de dialogue Progression.

Pour en savoir plus sur la fonction de régression par les moindres carrés ordinaires

Illustration

Utilisation

La sortie principale de cet outil est un fichier de rapport enregistré dans la fenêtre Résultats. Cliquez avec le bouton droit de la souris sur l'entrée Messages dans la fenêtre Résultats et sélectionnez Afficher pour afficher le rapport récapitulatif Régression exploratoire dans une boîte de dialogue de message.
Remarque :
Si cet outil fait partie d'un outil de modèle personnalisé, les tables facultatives apparaissent uniquement dans la fenêtre Résultats si elles sont définies comme paramètres de modèle avant l'exécution de l'outil.
L'outil des moindres carrés ordinaires génère également une classe d'entités en sortie et des tables facultatives contenant des coefficients et des diagnostics. Tous sont accessibles dans la fenêtre Résultats. La classe d'entités en sortie est ajoutée automatiquement à la table des matières et un rendu de type chaud/froid (hot/cold) est appliqué aux valeurs résiduelles du modèle. Une explication complète de chaque résultat en sortie est fournie dans Interprétation des résultats des moindres carrés ordinaires.
Les résultats de la régression à l'aide des moindres carrés ordinaires ne sont fiables que si vos données et le modèle de régression répondent à toutes les suppositions requises de manière inhérente par cette méthode. Consultez le tableau intitulé Problèmes de régression courants, conséquences et solutions dans la rubrique Principes de base de l'analyse de régression pour vous assurer que votre modèle est correctement spécifié.
Les variables dépendantes et explicatives doivent être des champs numériques contenant diverses valeurs. La méthode des moindres carrés ordinaires ne peut pas être résolue si les variables ont toutes la même valeur (lorsque toutes les valeurs d'un champ sont définies sur 9,0 par exemple). Les méthodes de régression linéaire telles que celle des moindres carrés ordinaires ne sont pas appropriées pour prévoir des résultats binaires (toutes les valeurs de la variable dépendante sont 1 ou 0, par exemple).
Le champ ID unique associe les prévisions du modèle à chaque entité. Par conséquent, les valeurs ID unique doivent être uniques pour chaque entité et, en général, doivent se trouver dans un champ associé de façon permanente à la classe d'entités. Si aucun champ ID unique n'est présent, il est facile d'en créer un en ajoutant un nouveau champ d'entier à votre table de classes d'entités et en calculant les valeurs du champ de sorte qu'elles soient égales à celles du champ FID/OID. Vous ne pouvez pas utiliser directement le champ FID/OID comme paramètre ID unique.
Chaque fois que l'autocorrélation spatiale des valeurs résiduelles de régression est statistiquement significative, le modèle des moindres carrés ordinaires est considéré comme mal spécifié et, par conséquent, les résultats de la régression par les moindres carrés ordinaires ne sont pas fiables. Exécutez l'outil Autocorrélation spatiale sur vos valeurs résiduelles de régression pour évaluer ce problème potentiel. L'autocorrélation spatiale statistiquement significative de valeurs résiduelles de régression indique presque toujours qu'une ou plusieurs variables explicatives clés manquent dans le modèle.
Etudiez les surestimations et sous-estimations évidentes dans les valeurs résiduelles de régression afin de trouver des indices permettant de déterminer s'il manque des variables dans votre modèle de régression. Il peut être bon d'exécuter l'outil Hot Spot Analysis sur les valeurs résiduelles pour mieux visualiser l'agrégation spatiale des surestimations et des sous-estimations.
Lorsqu'une spécification incorrecte est le résultat d'une tentative de modélisation de variables non stationnaires à l'aide d'un modèle global (la méthode des moindres carrés ordinaires est un modèle global), la régression pondérée géographiquement peut être utilisée pour améliorer les prévisions et pour mieux comprendre la non stationnarité (variation régionale) inhérente à vos variables explicatives.
Si le résultat d'un calcul est l'infini ou s'il est indéfini, la sortie pour les fichiers autres que des fichiers de formes sera Null. Pour les fichiers de formes, le résultat sera -DBL_MAX (-1,7976931348623158e+308, par exemple).
Le récapitulatif des diagnostics du modèle est enregistré dans le rapport récapitulatif des moindres carrés ordinaires et dans la table en sortie des diagnostics (générée uniquement si vous le souhaitez). Ces deux documents incluent des diagnostics pour le critère d'information d'Akaike corrigé (AICc), le coefficient de détermination, la statistique F de jointure, la statistique Wald, la statistique Breusch-Pagan de Koenker et la statistique Jarque-Bera. La table des diagnostics inclut également des valeurs "AIC non corrigé" et "Sigma carré".
Les tables en sortie facultatives des coefficients et/ou des diagnostics, si elles existent déjà, sont remplacées lorsque l'option de géotraitement Remplacer les résultats des opérations de géotraitement est sélectionnée.
Si vous le souhaitez, cet outil peut également générer un fichier PDF récapitulant les résultats. Les fichiers PDF n'apparaissent pas automatiquement dans la fenêtre Catalogue. Si vous souhaitez afficher des fichiers PDF dans la fenêtre Catalogue, ouvrez l'application ArcCatalog, sélectionnez l'option de menu Personnaliser, cliquez sur Options ArcCatalog et sélectionnez l'onglet Types de fichiers. Cliquez sur le bouton Nouveau type et, pour la valeur du paramètre Extension de fichier, spécifiez PDF comme indiqué ci-après.
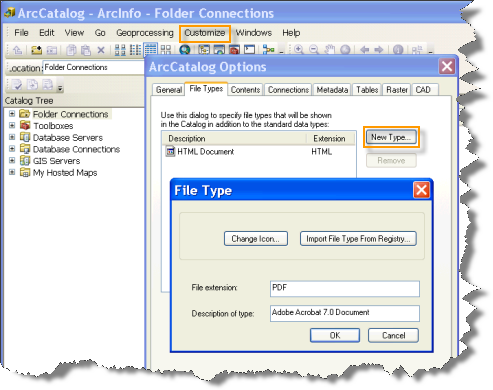
Sur des machines configurées avec les modules linguistiques d'ArcGIS pour l'arabe et d'autres langues qui s'écrivent de droite à gauche, vous remarquerez peut-être du texte manquant ou des problèmes de mise en forme dans le fichier de rapport en sortie (au format PDF). Ces problèmes sont traités dans cet article.
Les couches peuvent permettre de définir la classe d'entités en entrée. Lorsque vous utilisez une couche avec une sélection, seules les entités sélectionnées sont comprises dans l'analyse.

Syntaxe

OrdinaryLeastSquares_stats (Input_Feature_Class, Unique_ID_Field, Output_Feature_Class, Dependent_Variable, Explanatory_Variables, {Coefficient_Output_Table}, {Diagnostic_Output_Table}, {Output_Report_File})

Paramètre	Explication	Type de données
Input_Feature_Class	Classe d'entités qui contient les variables dépendantes et indépendantes pour l'analyse.	Feature Layer
Unique_ID_Field	Champ de nombre entier qui contient une valeur différente pour chaque entité dans la classe d'entités en entrée.	Field
Output_Feature_Class	Classe d'entités en sortie pour recevoir des estimations de variable dépendante et des résiduels.	Feature Class
Dependent_Variable	Champ numérique qui contient des valeurs pour la modélisation.	Field
Explanatory_Variables [Explanatory_Variables,...]	Liste des champs qui représentent des variables explicatives dans votre modèle de régression.	Field
Coefficient_Output_Table (Facultatif)	Chemin d'accès complet à une table facultative et où sont enregistrés des coefficients de modèle, des coefficients normalisés, des erreurs standard, ainsi que des probabilités pour chaque variable explicative.	Table
Diagnostic_Output_Table (Facultatif)	Chemin d'accès complet à une table facultative où est enregistré le récapitulatif des diagnostics du modèle.	Table
Output_Report_File (Facultatif)	Chemin d'accès au fichier PDF facultatif qui sera généré par l'outil. Ce fichier de rapport comprend des diagnostics de modèle, des diagrammes et des notes qui vous permettront de mieux interpréter les résultats obtenus à l'aide de l'outil Moindres carrés ordinaires.	File

Exemple de code

Exemple 1 d'utilisation de l'outil OrdinaryLeastSquares (fenêtre Python)

Le script de fenêtre Python ci-dessous montre comment utiliser l'outil OrdinaryLeastSquares.

import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID","olsResults.shp", 
                                 "GROWTH","LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                                 "olsCoefTab.dbf","olsDiagTab.dbf")

Exemple 2 d'utilisation de l'outil OrdinaryLeastSquares (script Python autonome)

Le script Python autonome ci-dessous illustre l'utilisation de l'outil Moindres carrés ordinaires.

# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
    # Set the current workspace (to avoid having to specify the full path to the feature classes each time)
    arcpy.env.workspace = workspace
    # Growth as a function of {log of starting income, dummy for South
    # counties, interaction term for South counties, population density}
    # Process: Ordinary Least Squares... 
    ols = arcpy.OrdinaryLeastSquares_stats("USCounties.shp", "MYID", 
                        "olsResults.shp", "GROWTH",
                        "LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
                        "olsCoefTab.dbf",
                        "olsDiagTab.dbf")
    # Create Spatial Weights Matrix (Can be based off input or output FC)
    # Process: Generate Spatial Weights Matrix... 
    swm = arcpy.GenerateSpatialWeightsMatrix_stats("USCounties.shp", "MYID",
                        "euclidean6Neighs.swm",
                        "K_NEAREST_NEIGHBORS",
                        "#", "#", "#", 6) 
                        
    # Calculate Moran's Index of Spatial Autocorrelation for 
    # OLS Residuals using a SWM File.  
    # Process: Spatial Autocorrelation (Morans I)...      
    moransI = arcpy.SpatialAutocorrelation_stats("olsResults.shp", "Residual",
                        "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE", 
                        "EUCLIDEAN_DISTANCE", "NONE", "#", 
                        "euclidean6Neighs.swm")
except:
    # If an error occurred when running the tool, print out the error message.
    print(arcpy.GetMessages())

Environnements

Informations de licence

ArcGIS Desktop Basic: Oui
ArcGIS Desktop Standard: Oui
ArcGIS Desktop Advanced: Oui

ArcMap

Moindres carrés ordinaires