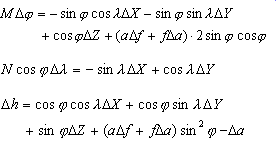Les méthodes de transformation par équation peuvent être classées selon les quatre types décrits ci-dessous.
Méthodes à trois paramètres
La méthode de transformation de datum la plus simple consiste en une transformation géocentrique ou à trois paramètres. La transformation géocentrique permet de modéliser les différences entre deux datums dans le système de coordonnées cartésiennes XYZ ou 3D. Un datum est défini avec son centre à 0,0,0. Le centre de l’autre datum est défini à une certaine distance (dx,dy,dz ou ΔX,ΔY,ΔZ) en mètres de l’autre datum.
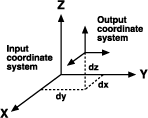
Généralement, les paramètres de transformation sont définis comme partant « d’un » datum local « vers » World Geodetic System (WGS) 1984 ou un autre datum géocentrique.
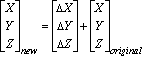
Les trois paramètres sont des translations linéaires et se définissent toujours en mètres.
Méthodes à sept paramètres
Une transformation de datum plus complexe et plus précise est possible en ajoutant quatre paramètres supplémentaires à une transformation géocentrique. Ces sept paramètres comprennent trois translations linéaires (dx,dy,dz), trois rotations angulaires autour de chaque axe (rx,ry,rz) et un facteur d’échelle.
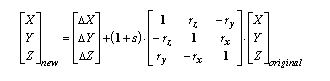
Les valeurs de rotation sont données en secondes décimales, tandis que le facteur d’échelle est en parts par million (ppm). Les valeurs de rotation peuvent être définies de deux façons différentes : positives dans le sens horaire ou anti-horaire quand vous regardez l’origine des systèmes XYZ.
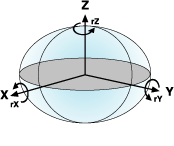
L’équation précédente correspond à la manière dont les États-Unis et l’Australie définissent les équations et s’appelle la transformation par rotation du cadre des coordonnées. Les rotations sont positives dans le sens anti-horaire. L’Europe suit une convention différente appelée la transformation par vecteur de position. Ces deux méthodes sont parfois désignées sous le nom de méthode Bursa Wolf. Dans le moteur de projection, les méthodes Cadre des coordonnées et Bursa Wolf sont identiques. Les méthodes Cadre des coordonnées et Vecteur de position sont gérées et la conversion des valeurs de transformation s’effectue facilement d’une méthode à l’autre, en changeant simplement les signes des trois valeurs de rotation. Par exemple, les paramètres de conversion à partir du datum WGS 1972 vers le datum WGS 1984 par la méthode du cadre des coordonnées sont (dans l’ordre : dx,dy,dz,rx,ry,rz,s) :
(0.0, 0.0, 4.5, 0.0, 0.0, -0.554, 0.227)Pour utiliser les mêmes paramètres avec la méthode Vecteur de position, changez le signe de la rotation pour obtenir les nouveaux paramètres suivants :
(0.0, 0.0, 4.5, 0.0, 0.0, +0.554, 0.227)Il est impossible, à partir des seuls paramètres, de déterminer la convention utilisée. Si vous employez la mauvaise méthode, vos résultats peuvent donner des coordonnées erronées. Le seul moyen de déterminer le mode de définition de ces paramètres consiste à effectuer une vérification à partir d’un point de contrôle dont les coordonnées sont connues des deux systèmes.
La méthode Molodensky-Badekas est une variation de la méthode à sept paramètres. Trois paramètres supplémentaires définissent l’origine XYZ de rotation. Parfois, ce point est également appelé origine du datum ou du système de coordonnées géographiques. Connaissant l’origine XYZ du point de rotation, vous pouvez calculer une transformation du cadre des coordonnées équivalente. Les valeurs dx, dy et dz changent, mais les valeurs de rotation et d’échelle restent inchangées.
Méthode Molodensky
La méthode Molodensky permet d’effectuer une conversion directe entre deux systèmes de coordonnées géographiques sans effectuer réellement de conversion vers un système XYZ. La méthode Molodensky nécessite l’utilisation de trois translations (dx,dy,dz) et les différences entre les demi-grands axes (Δa) et les aplatissements (Δf) des deux sphéroïdes. Le moteur de projection calcule automatiquement les différences de sphéroïdes en fonction des datums concernés.
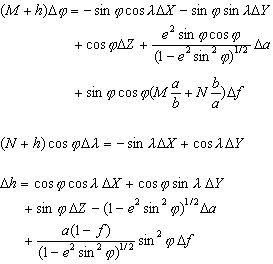
- h = hauteur ellipsoïdale (mètres)
- Φ = latitude
- λ = longitude
- a = demi-grand axe de la sphéroïde (mètres)
- b = demi-petit axe de la sphéroïde (mètres)
- f = aplatissement de la sphéroïde
- e = excentricité de la sphéroïde
M et N représentent, respectivement, le rayon méridien et le rayon du premier vertical pour une latitude donnée. Les équations correspondant à M et N sont les suivantes :
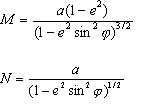
Vous déterminez Δλ et ΔΦ. Le moteur de projection ajoute automatiquement les résultats.
Méthode Molodensky abrégée
La méthode Molodensky abrégée est une version simplifiée de la méthode Molodensky. Examinez les équations ci-dessous :