Disponible avec une licence Spatial Analyst.
Un ensemble d'étapes conceptuelles peut être utilisé pour créer un modèle. Afin de comprendre le processus étape par étape, vous allez étudier un exemple de problème. En tant qu'urbaniste, vous êtes chargé de rechercher des localisations convenables pour une nouvelle école. Vous pouvez associer des outils de l'extension Spatial Analyst d'ArcGIS pour vous aider à identifier les sites potentiels.
Etape 1 : définition du problème
Pour résoudre un problème spatial, vous devez commencer par définir clairement le problème à résoudre ainsi que l'objectif à atteindre. Commencez avec un concept du résultat d’étude recherché pour visualiser les types de cartes que vous souhaitez obtenir.
Votre problème consiste à rechercher le meilleur emplacement pour le site d'un nouvel établissement scolaire. Vous devez générer deux cartes. La première identifie l’aptitude de chaque emplacement par rapport aux autres, il s’agit de la carte d’aptitude. La seconde, qui est dérivée de la carte d’aptitude, identifie l’emplacement réel où construire l’école en tenant compte des besoins fonctionnels de cette dernière (taille et forme souhaitée). Pour créer ces deux cartes, vous allez générer un modèle d’aptitude pondéré.
Pour vous aider à modéliser votre problème spatial, dessinez un schéma des étapes impliquées. Commencez par énoncer le problème. Au fur et à mesure de votre travail, vous compléterez le schéma en y ajoutant des objectifs, des modèles de processus et des jeux de données en entrée nécessaires pour atteindre votre but.
Etape 2 : décomposition du problème
Une fois le problème énoncé, scindez-le jusqu'à ce que vous identifiiez les étapes nécessaires pour le résoudre. Ces étapes correspondent aux objectifs à remplir.
Lorsque vous définissez les objectifs, pensez à comment vous allez les évaluer. Comment allez-vous évaluer la meilleure zone pour le nouvel établissement ? Dans cet exemple fictif de choix d’un site pour une école, l’un des facteurs essentiels consiste à minimiser le coût de développement. Il est plus économique d’effectuer des constructions sur certains types d’utilisation du sol, comme les surfaces actuellement considérées comme des champs ouverts, par rapport à des surfaces qui ont déjà connu un certain développement. Un autre facteur est le MNT, puisqu’il est généralement plus aisé d’effectuer des constructions sur des surfaces planes que sur des pentes escarpées. Étant donné que de nombreuses familles ayant déménagé en ville ont de jeunes enfants, il est préférable de situer l’emplacement à proximité d’installations de loisirs. Afin de distribuer les ressources dans la totalité de la ville, il est important de trouver un emplacement loin des écoles existantes. Pour répondre aux exigences fonctionnelles de l’école, le site potentiel doit être suffisamment grand pour l’école et son terrain. Davantage d’objectifs pourraient bien sûr être inclus, comme le coût d’achat du terrain ou l’implantation dans une zone présentant la plus haute densité d’enfants d’un âge donné, mais ce modèle est volontairement simplifié pour l’exemple.
Pour atteindre ces objectifs, vous devez connaître les informations suivantes :
- L'utilisation du sol est-elle appropriée dans ces emplacements ?
- Où sont les emplacements dont le terrain est relativement plat ?
- Ces emplacements sont-ils assez proches d'installations récréatives ?
- Sont-ils assez éloignés des écoles existantes ?
L'utilisation du sol est-elle appropriée dans ces emplacements ?
Vous devez déterminer les caractéristiques d'un type d'utilisation du sol approprié sur lequel construire l'école. Ce processus est subjectif et fonction de votre problème. Ici, les terres agricoles sont considérées comme les terrains de construction les moins chers et donc privilégiés. Viennent ensuite les terres stériles, puis les zones à arbustes, les forêts et les zones déjà construites. Aucun modèle de processus n'est impliqué ici, seulement l'identification du jeu de données d'utilisation du sol en entrée et la détermination du type d'utilisation du sol le plus approprié.
- Jeu de données nécessaire en entrée : Utilisation du sol
Où sont les emplacements dont le terrain est relativement plat ?
Pour trouver les zones dont le terrain est relativement plat, vous devez créer une carte qui affiche la pente du terrain. Ici, le modèle de processus passe par le calcul de la pente du terrain.
- Jeu de données nécessaire en entrée : Altitude
Ces emplacements sont-ils assez proches d'installations récréatives ?
Vous savez qu'il est préférable de construire l'école à proximité d'installations récréatives. Vous devez donc créer une carte qui affiche les distances par rapport à ces installations pour situer éventuellement l'école dans les zones avoisinantes. Ici, le modèle de processus passe par le calcul des distances depuis les installations récréatives.
- Jeu de données nécessaire en entrée : Emplacement des installations récréatives
Sont-ils assez éloignés des écoles existantes ?
Il est préférable de situer l'école à l'écart des établissements déjà présents pour éviter d'empiéter sur leurs zones de captation. Vous devez donc créer une carte indiquant la distance par rapport aux écoles. Ici, le modèle de processus passe par le calcul de la distance par rapport aux écoles existantes.
- Jeu de données nécessaire en entrée : Emplacement d'écoles existantes
Etape 3 : exploration des jeux de données en entrée
Après avoir scindé le problème en plusieurs objectifs et modèles de processus et après avoir déterminé les jeux de données nécessaires, vous devez explorer ces derniers pour en comprendre le contenu. Pour ce faire, vous devez identifier les attributs contenus dans les jeux de données et entre les jeux de données qui contribuent le plus à la résolution du problème et à la recherche de tendances dans les données.
L'exploration des données vous mettra sur la voie quant aux zones appropriées pour situer l'école, à la pondération des attributs en entrée et aux modifications à apporter au processus de modélisation. Les données vous indiquent les emplacements des écoles existantes et des installations récréatives et, le jeu de données d'altitudes vous donne une indication des altitudes les plus élevées. Le jeu de données d'utilisation du sol vous informe sur les types d'utilisation du sol présents dans la zone concernée et sur leur emplacement par rapport aux autres jeux de données.
Etape 4 : exécution de l'analyse
Vous avez déterminé vos objectifs, les éléments et leurs interactions, les modèles de processus et les jeux de données nécessaires. Vous êtes donc prêt à effectuer l'analyse.
De nombreuses tâches pouvant être résolues par ArcGIS sont présentées dans l'ouvrage Esri Guide to GIS Analysis paru chez Esri Press .
.
Voici un diagramme de traitement général pour cet exemple d’identification de l’emplacement idéal d’une nouvelle école. Le texte d’accompagnement détaille davantage chacune des étapes.

Création d'une carte d'aptitude
La création d'une carte d'aptitude vous permet d'obtenir une valeur d'aptitude pour chaque emplacement sur la carte.
Une fois que vous avez créé les couches nécessaires (dans cet exemple, les couches sont Land use (Utilisation du sol), Slope (Pente), Distance to recreation sites (Distance par rapport aux installations récréatives) et Distance to schools (Distance par rapport aux écoles)) à votre analyse, comment ces couches créées sont-elles associées pour créer une carte classée de surfaces potentielles pour situer l’école ? Vous devez comparer les valeurs entre les couches. Pour ce faire, transformez les valeurs des différents jeux de données en une échelle commune.
Chaque emplacement de chaque couche est classé par son degré d’aptitude en tant qu’emplacement pour la nouvelle école. Par exemple, vous pouvez affecter une valeur à chaque emplacement de chaque couche selon une échelle de 1 à 10, 10 étant le meilleur classement.
Cette échelle s'appelle une "échelle d'aptitude". Utilisez la valeur NoData pour écarter les zones qui ne doivent pas être prises en compte. Le fait d'affecter à toutes les mesures la même échelle numérique leur donne la même importance dans la détermination des emplacements les plus appropriés. Au départ, le modèle est élaboré de cette manière. Par la suite, lorsque vous testerez d’autres scénarios, des facteurs de pondération différents pourront être appliqués aux couches pour approfondir l’exploration des données et de leurs relations.
Création d'échelles d'aptitude
Comme c’est le cas de cet exemple, de nombreuses unités de mesure des échelles d’aptitude sont synthétiques. Quelles que soient les unités de mesure utilisées pour l’échelle d’aptitude, cette dernière est une mesure classée de l’aptitude, ou de la préférence, de la meilleure à la pire. Les unités doivent être basées sur un élément pouvant être mesuré, par exemple, la distance par rapport aux écoles. Dans de nombreux cas, cependant, il s’agit d’une mesure subjective de l’aptitude d’une certaine distance par rapport à une école pour situer une autre école.
Il existe des unités de mesure naturelles qui sont communément associées à certains objectifs. Le coût en est un bon exemple, mais doit être défini suffisamment en détail. Dans une étude sur l'aptitude d'un bâtiment, un objectif de coût immobilier faible serait mesuré sur une échelle en dollars. Veillez à définir l'échelle de manière adéquate. Pour un élément aussi connu que le dollar, il faut prendre en compte d'autres variables, par exemple s'il s'agit de dollars américains, australiens ou d'un taux de change entre devises.
De nombreuses échelles ne sont pas des relations linéaires bien qu'elles soient souvent présentées de cette manière pour gagner du temps et réaliser des économies ou parce que toutes les options n'ont pas été envisagées. Par exemple, si vous affectez une échelle à une distance de déplacement, un déplacement de 1,5 ou 10 kilomètres ne serait pas classé comme une aptitude de 10, 5 et 1 si le déplacement se faisait à pied. Certaines personnes jugeront qu'une marche de 5 kilomètres n'est que deux fois plus fatigante qu'une marche de 1 kilomètre, et d'autres dix fois plus.
Lorsque vous élaborez une échelle d'aptitude, demandez l'avis de personnes bien informées pour identifier les deux extrêmes d'un scénario et autant de points intermédiaires que possible. Ces personnes doivent bien connaître l'objectif à l'étude. Par exemple, il est plus intéressant de demander à des usagers leur opinion sur le temps qu'ils souhaiteraient mettre pour se rendre de leur domicile à leur travail, que de demander à un agent les heures à laquelle la circulation est la plus mauvaise.
Consultez GIS and Multicriteria Decision Analysis de Jacek Malczewski pour plus d'informations sur la façon de gérer les objectifs en conflit et les critères d'évaluation.
Classement des entrées
Une fois les différentes entrées préparées, vous devez les transformer et les adapter à l’échelle commune.
Classement des zones dont le type d'utilisation du sol est approprié
Pour classer la carte représentant les types d’utilisation du sol, faites appel à l’outil Reclassify (Reclassification). Puisqu'il est préférable de construire sur certains types d'utilisation du sol en raison des coûts, vous devez déterminer le mode de classement des valeurs.
Ici, vous devez déterminer les types d'utilisation du sol les plus appropriés. Ce processus est subjectif car il dépend de votre étude. Le plus simple est de décider ce qui est le mieux approprié et ce qui l'est le moins. Ensuite, classez par ordre de préférence les types d'utilisation du sol restants. Procédez ainsi jusqu'à ce que tous les types d'utilisation soient classés. Les utilisations du sol de type eau et marécages ont été exclues de l'analyse car vous ne pouvez pas construire sur de l'eau et devez respecter certaines restrictions quant aux constructions sur des marécages. L'illustration ci-dessous indique le classement des types d'utilisation du sol.
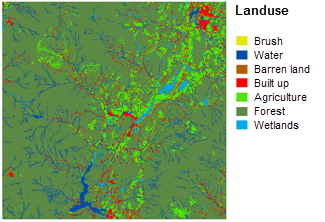
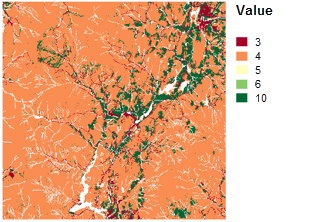
Classement des zones dont le terrain est relativement plat
Pour éviter les MNT raides et rechercher les zones dont le terrain de construction est relativement plat, vous devez connaître la pente du terrain. L’outil Slope (Pente) crée ce type de carte en identifiant pour chaque cellule le taux de variation maximal des valeurs de chaque cellule par rapport aux cellules voisines. Le raster généré enregistre la pente sous forme de valeurs variables à virgule flottante. Étant donné que la préférence varie directement en fonction des modifications de la valeur de pente, l’outil Redimensionner par fonction est utilisé pour classer cette carte via l’application de la fonction Linear. Puisqu’il est préférable de situer l’école sur un terrain relativement plat, affectez la valeur 1 aux emplacements dont la pente est raide et la valeur 10 aux emplacements dont la pente est douce. Les valeurs entre les deux sont ajustées en mode linéaire, comme indiqué par l’illustration suivante :

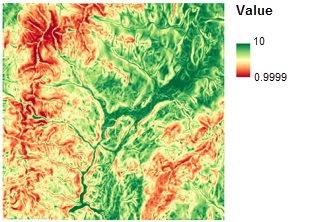
Classement des zones à proximité d'installations récréatives
Pour situer l'école près des installations récréatives, vous devez connaître la distance qui les sépare. L’outil Euclidean Distance (Distance euclidienne) crée ce type de carte en calculant la distance en ligne droite (euclidienne) entre un emplacement et les installations de loisirs les plus proches. Il en résulte un jeu de données raster dans lequel chaque cellule représente la distance aux installations récréatives les plus proches. Étant donné que les valeurs en entrée représentent des distances continues, vous devez utiliser l’outil Redimensionner par fonction pour classer cette carte. Comme il est de loin préférable de choisir un emplacement proche des installations de loisirs, la fonction MSSmall est appliquée. Cela permet d’affecter des valeurs de préférences bien plus élevées aux emplacements situés à proximité des installations de loisirs, les emplacements plus éloignés étant les moins préférés. À chaque modification métrique de la distance par rapport aux installations de loisirs, la préférence varie constamment, comme le montre l’illustration suivante :
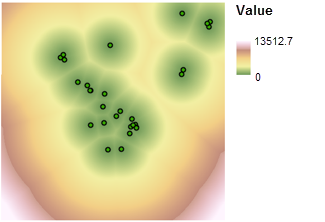
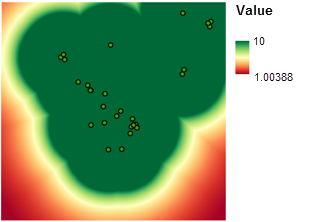
Pour en savoir plus sur l'analyse de distance en ligne droite
Classement des zones éloignées d'écoles existantes
Pour éviter les zones de captation d'autres écoles, vous devez connaître la distance qui les sépare de l'emplacement à rechercher. L'outil Distance euclidienne crée ce type de carte en calculant la distance en ligne droite entre un emplacement et l'école la plus proche. Il en résulte un jeu de données raster dans lequel chaque cellule représente la distance à l'école la plus proche. Pour classer cette carte, utilisez une fois encore l’outil Rescale by Function (Redimensionner par fonction). Puisqu’il est préférable de trouver un emplacement éloigné des écoles existantes, la fonction Large est utilisée pour donner la valeur 1 aux distances les plus proches des écoles existantes et la valeur 10 aux distances les plus éloignées des écoles existantes. Grâce à la fonction Large, les préférences augmentent constamment avec chaque mètre de distance supplémentaire par rapport à l’école, comme le montre l’illustration suivante :
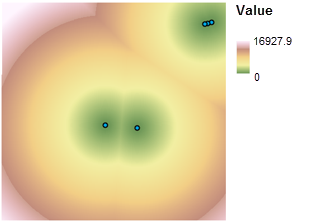
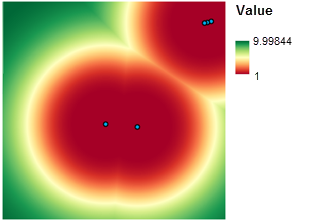
Regroupement des cartes d'aptitude
La dernière étape du modèle d’aptitude consiste à combiner les sorties transformées (les cartes d’aptitude) des types d’utilisation du sol, de la pente, de la distance par rapport aux installations de loisirs et de la distance par rapport aux écoles.
Pour prendre en compte le fait que certains objectifs pèsent plus que d'autres dans le modèle d'aptitude, vous pouvez pondérer les jeux de données. Vous donnez aux jeux de données plus importants un pourcentage d'influence (pondération) plus élevé. Si tous les jeux de données sont d'importance égale, vous pouvez attribuer à tous la même pondération.
Dans l'exemple, vous savez, d'après l'examen du problème, que le premier objectif à remplir est de situer l'école près d'installations récréatives, et le deuxième est de la situer à l'écart des écoles existantes. Les pourcentages d'influence suivants seront attribués aux cartes d'aptitude. Les valeurs entre parenthèses correspondent au pourcentage divisé par 100 pour normaliser les valeurs. Cette valeur normalisée est utilisée comme multiplicateur pour chaque carte d’aptitude.
Pourcentages d'aptitude
| Facteurs d'aptitude | Influence en pourcentage | Pourcentages normalisés |
|---|---|---|
Distance classée par rapport aux installations de loisirs | 50% | (0.5) |
Distance classée par rapport aux écoles | 25% | (0.25) |
Pente classée | 12,5% | (0.125) |
Types d’utilisation du sol classés | 12,5% | (0.125) |
La carte d’aptitude de la distance par rapport aux installations de loisirs a une influence de 50 % (0,5) sur le résultat final, et la carte de la distance par rapport aux écoles une influence de 25 % (0,25). Les facteurs de pente et de types d’utilisation du sol ont tous les deux une influence de 12,5 % (0,125). Comme dans l'affectation d'échelles d'aptitude, l'affectation de pondérations est un processus subjectif qui dépend des objectifs les plus importants de votre étude.
La carte d'aptitude finale est produite en associant toutes les autres cartes. Vous pouvez attribuer des pondérations en même temps que vous regroupez les cartes d'aptitude. La carte d'aptitude définitive pour la localisation de sites pour l'école est illustrée ci-dessous. La plupart des localisations convenables sont en vert foncé. Les emplacements les moins adaptés sont en nuances de rouge.

Vous pouvez faire appel à l'algèbre spatial pour pondérer et combiner des jeux de données. Vous pouvez aussi utiliser l’outil Weighted Overlay (Superposition pondérée) ou Weighted Sum (Somme pondérée). Si vous utilisez un outil dans un modèle, vous avez la possibilité de revenir en arrière et de modifier facilement les pondérations (les pourcentages d’influence) et les valeurs d’échelle que vous avez définies. La connexion d’outils de géotraitement à l’intérieur d’un modèle signifie que vous avez simplement besoin de créer le modèle une fois, vous pouvez ensuite modifier les valeurs de paramètre pour les expérimenter avec les différents résultats.
Localisation de l’école
L’étape finale de ce traitement de modélisation est de localiser réellement l’école. La surface d’aptitude finale classe les attributs de chaque emplacement en fonction du type d’utilisation du sol, de la pente, de la distance par rapport aux installations de loisirs et de la distance par rapport aux écoles. L’école proposée doit toutefois répondre à des exigences spatiales pour pouvoir fonctionner efficacement.
Le meilleur site de votre école doit se trouver sur un terrain de 150 acres contigus afin de pouvoir accueillir les terrains de sport. Pour des raisons liées à la construction et à l’efficacité de la maintenance, la configuration du site doit être relativement compacte.
L’outil Locate Regions (Localiser les régions) est utilisé sur la surface d’aptitude finale pour rechercher le meilleur site de 150 acres.
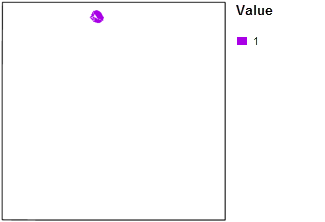
Comparez le site proposé à la carte d’aptitude de l’étape précédente.
Etape 5 : vérification du résultat
Une fois que vous obtenez les résultats d'une analyse spatiale, vous devez vérifier s'ils sont corrects. Pour ce faire, visitez les sites candidats, dans la mesure du possible. Souvent, les résultats obtenus omettent un facteur déterminant. Par exemple, la présence d’un élevage de poulets en amont du site dont les odeurs constituent une nuisance ou encore une interdiction de construire sur le terrain souhaité dont vous n’aviez pas connaissance. Dans l'un ou l'autre des cas, vous devez ajouter ces informations à l'analyse.
Etape 6 : mise en œuvre des résultats
La dernière étape du modèle spatial est l'implémentation du résultat, à savoir le démarrage de la planification et de la construction de la nouvelle école à l'emplacement choisi.
Pour en savoir plus sur la modélisation d’adéquation, reportez-vous à la rubrique Comprendre le processus de modélisation d’adéquation  , section Analyse appliquée.
, section Analyse appliquée.
Bibliographie
Malczewski, J. GIS and Multicriteria Decision Analysis. Wiley & Sons, 1999.