Les transformations procèdent au déplacement ou à la translation des données dans un système de coordonnées. Elles sont souvent utilisées pour convertir des unités inconnues de numériseur ou de scanner en coordonnées géographiques. Les transformations permettent également de convertir des unités dans un système de coordonnées, par exemple des pieds en mètres. Pour convertir des données entre des systèmes de coordonnées, par exemple géographique en UTM, vous devriez plutôt projeter les données.
Les fonctions de transformation s’appuient sur la comparaison des coordonnées des points source et de destination (également appelés points de contrôle) au sein d’éléments graphiques spéciaux, appelés liens de déplacement. Pour des transformations, les emplacements source et de destination des liens permettent d’élaborer les formules de transformation. Vous pouvez créer ces liens de manière interactive, en pointant vers des emplacements source et des emplacements de destination connus, ou encore en chargeant un fichier texte de liens ou un fichier de points de contrôle.
Lorsque vous créez des liens pour des transformations, vous essayez d’apparier le même emplacement dans les emplacements source et de destination. Par exemple, vous détenez une couche de routes que vous essayez de transformer ou de translater vers l’emplacement d’autres données pouvant contenir une photographie aérienne. Lorsque vous créez des liens de déplacement, vous positionnez le début à une intersection de la couche de routes et la fin au niveau de l’intersection correspondante sur l’image. Il n’est pas nécessaire que les liens commencent ou se terminent sur des entités. Souvent, la distance entre les emplacements source et de destination est très grande.
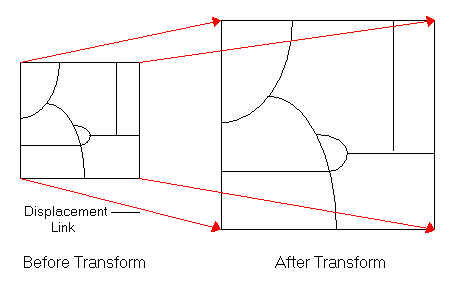
Par défaut, ArcMap prend en charge trois types de transformations : affine, projective et d’Helmert.
Transformation affine
Une transformation affine permet de mettre à l’échelle de façon non uniforme (différenciée) les données, de les désaxer, de les faire pivoter et de les convertir. Le graphique ci-après illustre les quatre changements possibles :
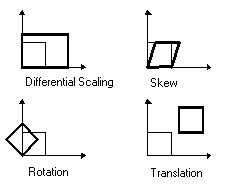
La fonction de transformation affine est la suivante :
x’ = Ax + By + C y’ = Dx + Ey + F où x et y sont les coordonnées de la couche en entrée et x’ et y’ les coordonnées transformées. A, B, C, D, E et F sont déterminés en comparant l’emplacement des points de contrôle source et de destination. Ces paramètres mettent à l’échelle, désaxent, font pivoter et convertissent les coordonnées de couche. Cette méthode nécessite au moins trois liens. Il s’agit de la méthode recommandée pour la plupart des transformations.
La transformation affine nécessite au moins trois liens de déplacement.
Transformation d'Helmert
La transformation d’Helmert met à l’échelle, fait pivoter et convertit les données. Elle ne met pas à l’échelle les axes de manière indépendante et n’introduit pas de déformation. Elle maintient les proportions des entités transformées, ce qui est essentiel si vous désirez préserver la forme relative des entités.
La fonction de la transformation d’Herbert est la suivante :
x’ = Ax + By + C y’ = -Bx + Ay + Fwhere
A = s * cos t B = s * sin t C = translation in x direction F = translation in y direction and
s = scale change (same in x and y directions) t = rotation angle, measured counterclockwise from the x-axisLa transformation d’Helmert nécessite un minimum de deux liens de déplacement. Toutefois, au moins trois liens sont nécessaires pour générer la racine carrée de l’erreur quadratique moyenne (EQM).
Transformation projective
La transformation projective est établie à partir d’une formule plus complexe nécessitant au moins quatre liens de déplacement.
x’ = (Ax + By + C) / (Gx + Hy + 1) y’ = (Dx + Ey + F) / (Gx + Hy + 1) Cette méthode permet de transformer les données capturées directement à partir de photographies aériennes. Pour plus d’informations, reportez-vous à l’un des textes photogrammétriques répertoriés dans les références d’aide sur l’ajustement spatial.
Présentation de l’erreur résiduelle et de l’erreur quadratique moyenne
Les paramètres de transformation constituent un compromis entre les points de contrôle source et les points de contrôle de destination. Si vous appliquez les paramètres de transformation aux points de contrôle source réels, les emplacements en sortie transformés ne correspondent pas aux véritables emplacements des points de contrôle en sortie. Il s’agit d’une erreur résiduelle ; elle mesure la différence entre les emplacements véritables et les emplacements transformés des points de contrôle en sortie. Cette erreur est générée pour chaque lien de déplacement.
La racine carrée de l’erreur quadratique moyenne est calculée pour chaque transformation effectuée ; elle indique la qualité de la transformation dérivée. L’exemple suivant illustre l’emplacement relatif de quatre points de contrôle de destination et des points de contrôle source transformés :
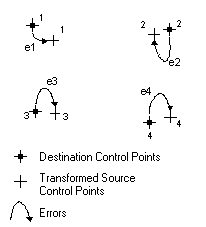
L’erreur QM mesure les erreurs entre les points de contrôle de destination et les emplacements transformés des points de contrôle source.
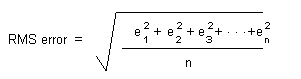
La transformation est dérivée à l’aide de la méthode de compensation des moindres carrés pour créer un nombre plus important de liens que nécessaire. Il est obligatoire de définir au moins trois liens pour créer une transformation qui génère une erreur QM.
Généralement, plus vous placez de liens pour une transformation, plus celle-ci est précise. Vous pouvez vérifier la précision de la transformation en consultant les erreurs QM dans la table des liens.
Transformations aveugles
Vous devrez parfois effectuer un ajustement, généralement une transformation, dans lequel l’emplacement de destination ne comporte aucune donnée, ce qui vous empêche de placer de façon interactive la fin d’un lien de déplacement. Par exemple, vous avez peut-être numérisé certaines données et souhaitez les transformer d’unités de numériseur en coordonnées terrestres. Dans ce cas, vous connaissez sans doute les coordonnées terrestres des emplacements de certaines entités de vos données telles qu’une intersection de routes ou l’emplacement d’un puits.
Vous pouvez néanmoins configurer la transformation en créant des liens de déplacement dont le début est placé à des emplacements connus et la fin sur des points temporaires dans l’espace. Vous pouvez alors utiliser la table de liens pour mettre à jour les coordonnées de destination de ces liens afin qu’ils correspondent aux emplacements réels.