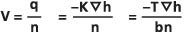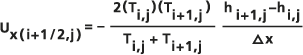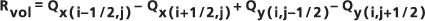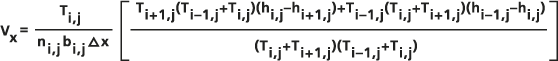Disponible avec une licence Spatial Analyst.
Les outils Flux de Darcy et Vitesse de Darcy, en association avec les outils Suivi de particules et Concentration, permettent d’effectuer une modélisation d’advection-dispersion rudimentaire des éléments d’une nappe phréatique. Cette méthodologie modélise les flux bidimensionnels, verticalement mélangés, horizontaux et permanents, sachant que la hauteur est indépendante de la profondeur.
Calculs de flux de Darcy
Les équations utilisées dans le calcul du flux de Darcy sont décrites dans les sections suivantes.
Calcul du débit et de la vitesse
Selon la loi de Darcy, la vitesse de Darcy q en milieu poreux est calculée à partir de la conductivité hydraulique K et du gradient de hauteur
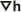(variation de hauteur par unité de longueur dans le sens de l’écoulement dans un aquifère isotrope) comme suit :- q = -K
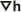
où K peut être calculé d’après la transmissivité T et l’épaisseur b selon l’équation K = T/b.
Cette vitesse q, exprimée en volume/temps/surface, est également appelée débit spécifique, flux volumétrique ou vitesse de filtration. Bear (1979) la définit comme étant le volume d’eau s’écoulant par unité de temps à travers une unité de surface de la section mouillée, perpendiculairement au sens d’écoulement.
- q = -K
Étroitement lié à ce flux volumétrique, le flux de l’aquifère U correspond au débit par unité de largeur de l’aquifère (avec les unités de volume/temps/longueur) :
- U = -T
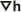
Cette construction suppose que la hauteur est indépendante de la profondeur de sorte que le flux est horizontal.
- U = -T
La vitesse moyenne du fluide à l’intérieur des pores, appelée vitesse d’infiltration V, est le rapport de la vitesse de Darcy par la porosité utile du milieu :
Avec l’outil Flux de Darcy, c’est cette vitesse d’infiltration V qui est calculée pour chaque cellule. Dans le cas de la cellule i,j, le flux aquifère U est calculé pour chacune des quatre parois de cellule, sur la base de la différence de hauteur entre deux cellules adjacentes et de la moyenne harmonique des transmissivités Ti+1/2,j (Konikow et Bredehoeft, 1978), qui sont considérées comme étant isotropiques.
Par exemple, pour l’élément x de
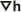, l’équation entre les cellules i,j et i+1,j est formulée comme suit :- δh/δx ≈ (hi+1 - hi) / Δx
Cette formule est illustrée dans les graphiques ci-dessous.
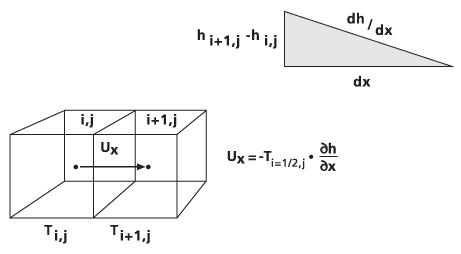
Calcul du volume résiduel
Dans le calcul de parois de cellule ci-après, le flux de l’aquifère entre la cellule i,j et la cellule i+1,j s’écoule parallèlement à la direction x selon l’équation suivante :
Pour déterminer le volume résiduel d’une nappe phréatique, il convient de calculer le débit de cette dernière à travers la paroi de la cellule. Ce débit Q x(i+1/2) est calculé d’après le flux aquifère U et la largeur de la paroi de la cellule Δy comme suit :
- Qx(i+1/2,j) = Ux(i+1/2,j) Δy
Des valeurs similaires sont obtenues pour les quatre parois de cellule. Ces valeurs permettent de calculer le volume résiduel de la nappe phréatique Rvol de la cellule, qui est écrit dans le raster en sortie. Cette valeur représente l’excédent (ou, dans le cas d’un nombre négatif, le déficit) hydrique à l’intérieur de chaque cellule compte tenu du flux net de la cellule, selon l’équation suivante :
Théoriquement, cette valeur résiduelle Rvol doit être de zéro pour toutes les cellules. Lorsque vous examinez le raster en sortie contenant les valeurs résiduelles, prêtez attention aux valeurs éloignées de zéro. Des valeurs résiduelles positives ou négatives élevées dénotent une production ou une perte de masse, ce qui est contraire au principe de continuité, et semblent indiquer une incohérence entre les données de hauteur et les données de transmissivité. Une certaine régularité dans les valeurs résiduelles positives ou négatives suggère la présence de sources ou de cuvettes non identifiées. Veillez à diminuer les valeurs résiduelles avant de poursuivre la modélisation. En règle générale, les corrections sont apportées au champ de transmissivité de manière à réduire les valeurs résiduelles.
Calcul des vecteurs flux
Les équations utilisées dans l’outil Flux de Darcy pour le calcul des vecteurs flux de chaque cellule sont condensées d’après la moyenne arithmétique de Ux(i-1/2,j) et Ux(i+1/2,j), divisée par la porosité ni,j et l’épaisseur bi,j de la cellule centrale, pour obtenir une valeur de vitesse d’infiltration Vx au centre :
Il existe une équation similaire pour calculer V y au centre :
Ce centrage est effectué de manière à respecter la convention selon laquelle les valeurs stockées représentent les valeurs au centre de la cellule. Ces valeurs sont converties en direction et magnitude dans les coordonnées géographiques, pour leur stockage dans les rasters de direction et de magnitude en sortie.
Dans le cas de cellules de délimitation du raster dans lesquelles les informations sont incomplètes, les valeurs de vitesse sont simplement récupérées par copie de la cellule intérieure la plus proche.
Valeurs de porosité
Les tableaux suivants récapitulent certaines des valeurs de porosité et de conductivité hydraulique pour divers milieux géologiques.
Tableau 1 : Conductivités hydrauliques de milieux non consolidés
| Moyenne | K (m/s) |
|---|---|
Gravier grossier | 10-1 - 10-2 |
Sable et gravier | 10-1 - 10-5 |
Sable fin, microgrès, lœss | 10-5 - 10-9 |
Argile, argile schisteuse, argile à blocaux | 10-9 - 10-13 |
Tableau 2 : Conductivités hydrauliques de milieux consolidés
| Moyenne | K (m/s) |
|---|---|
Calcaire dolomitique |
10-3 - 10-5 |
Craie altérée |
10-3 - 10-5 |
Craie non altérée |
10-6 - 10-9 |
Calcaire |
10-5 - 10-9 |
Grès |
10-4 - 10-10 |
Granite, gneiss, basalte compact |
10-9 - 10-13 |
Tableau 3 : Porosité des milieux géologiques
| Moyenne | Porosité totale |
|---|---|
Granite et gneiss non altérés | 0,0002 - 0,018 |
Quartzite | 0,008 |
Argile schisteuse, ardoise, micaschiste | 0,005 - 0,075 |
Calcaire, dolomie primaire | 0,005 - 0,125 |
Dolomie secondaire | 0,10 - 0,30 |
Craie | 0,08 - 0,37 |
Grès | 0,035 - 0,38 |
Tuf volcanique | 0,30 - 0,40 |
Sable | 0,15 - 0,48 |
Argile | 0,44 - 0,53 |
Argile gonflante, microgrès | jusqu’à 0,90 |
Terre arable cultivée | 0,45 - 0,65 |
D’autres valeurs tabulées de porosité et de conductivité hydraulique sont données dans les travaux de Freeze et Cherry (1979). Un récapitulatif de la porosité et de la transmissivité de diverses formations spécifiques décrites dans les ouvrages est présenté par Gelhar et al. (1992). Une discussion détaillée sur la porosité dans les matières sédimentaires est publiée par Blatt et al. (1980). Une discussion complète sur la modélisation de l’advection-dispersion à partir de ces fonctions est présentée par Tauxe (1994).
Exemples
La séquence typique pour la modélisation de la dispersion de la nappe phréatique consiste à utiliser dans l’ordre les outils Flux de Darcy, Suivi de particules puis Concentration.
- Voici un exemple des paramètres à configurer dans la boîte de dialogue de l’outil Flux de Darcy :
Raster de hauteur de la nappe en entrée : head
Input effective formation porosity raster (Raster de porosité effective de la formation en entrée) : poros
Input saturated thickness raster (Raster d’épaisseur saturée en entrée) : thickn
Raster de transmissivité de la formation en entrée : transm
Raster de volume résiduel de la nappe en sortie : resid1
Raster de direction en sortie : dir1
Raster de magnitude en sortie : mag1
- Voici un exemple des paramètres à configurer dans la boîte de dialogue de l’outil Vitesse de Darcy :
Raster de hauteur de la nappe en entrée : head
Input effective formation porosity raster (Raster de porosité effective de la formation en entrée) : poros
Input saturated thickness raster (Raster d’épaisseur saturée en entrée) : thickn
Raster de transmissivité de la formation en entrée : transm
Raster de direction en sortie : dir1
Raster de magnitude en sortie : mag1
Bibliographie
Bear, J. Hydraulics of Groundwater. McGraw-Hill. 1979
Blatt, H., G. Middleton, and R. Murray. Origin of Sedimentary Rocks, 2nd Ed. Prentice-Hall. 1980
Freeze, R. A., and J. A. Cherry. Groundwater. Prentice-Hall. 1979
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. « A Critical Review of Data on Field-Scale Dispersion in Aquifers. » Water Resources Research, 28 no. 7: 1955-1974. 1992.
Konikow, L. F. and J. D. Bredehoeft. « Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water », USGS Techniques of Water Resources Investigations, Book 7, Chap. C2, U.S. Geological Survey, Washington, D.C. 1978.
Marsily, G. de. Quantitative Hydrogeology. Academic Press. 1986.
Tauxe, J. D. « Porous Medium Advection-Dispersion Modeling in a Geographic Information System ». Doctoral Dissertation in Civil Engineering. The University of Texas at Austin, 1994.