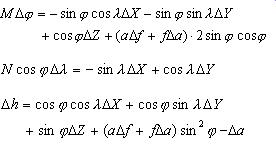数式に基づく変換方式は、以下の 4 種類に分類することができます。
3 パラメータ変換
最も単純な基準面変換方式は、地心の変換(つまり、3 つのパラメータによる変換)です。地心変換では、XYZ 座標系または 3 次元直交座標系によって 2 つの測地基準系間の差をモデリングします。一方の測地基準系の中心は 0,0,0 で定義され、もう一方の測地基準系の中心はそこから何メートル離れているか(dx,dy,dz または ΔX,ΔY,ΔZ)で定義されます。
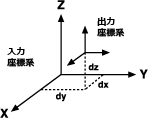
通常、変換パラメータは、ローカル測地基準系から World Geodetic System(WGS)1984 または別の地心測地基準系への間で定義されています。
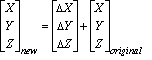
これら 3 つのパラメータはラインのシフトなので、常にメートル単位で表されます。
7 パラメータ変換
より複雑で精度の高い基準面変換を行うには、地心変換にさらに 4 つのパラメータを追加します。7 つのパラメータのうち、3 つは線形シフト(dx,dy,dz)、3 つはそれぞれの軸を中心とした回転角(rx,ry,rz)、最後の 1 つは縮尺係数です。
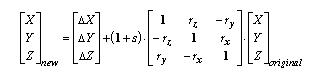
回転値はデシ秒で表され、縮尺係数は 100 万分の 1 単位(ppm)で表されます。回転値の定義には、2 つの方法があります。XYZ 座標系の原点に向かって時計回りまたは反時計回りに正の値として定義することができます。
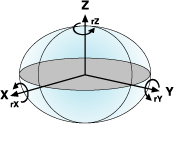
従来の数式は、アメリカとオーストラリアで定義されていたもので、Coordinate Frame 回転変換と呼ばれています。回転は反時計回りで正の値になります。ヨーロッパでは、Position Vector 変換と呼ばれる別の規約が使用されています。いずれの方式とも Bursa-Wolf 変換と呼ばれることがあります。投影エンジンでは、Coordinate Frame 変換も Bursa-Wolf 変換も同じものです。Coordinate Frame 変換と Position Vector 変換の両方がサポートされている場合、3 つの回転値を変更するだけで一方からもう一方の変換方式へ値を簡単に変換することができます。たとえば、Coordinate Frame 変換で WGS 1972 測地基準系から WGS 1984 測地基準系に変換するパラメータ(dx,dy,dz,rx,ry,rz,s の順)は以下のとおりです。
(0.0, 0.0, 4.5, 0.0, 0.0, -0.554, 0.227)Position Vector 変換で同じパラメータを使用するには、回転値の符号を変更します。新規のパラメータは以下のとおりです。
(0.0, 0.0, 4.5, 0.0, 0.0, +0.554, 0.227)パラメータだけでは、どの規約が使用されているかを判別することができません。誤った変換方式を使用すると、結果として精度の低い座標が返されることがあります。パラメータがどのように定義されているかを判別するには、2 つの変換方式で認識された座標を有する基準点を確認するしかありません。
Molodensky-Badekas 変換は、7 パラメータ変換の一種です。この変換方式には、回転の XYZ 原点を定義する 3 つのパラメータがさらに追加されます。このポイントは測地基準(つまり地理座標系)の原点と呼ばれることもあります。回転のXYZ原点がわかっていれば、そこから同等のCoordinate Frame 変換を算出することができます。dx 値、dy 値、および dz 値は変わりますが、回転値と縮尺値は変わりません。
Molodensky 変換
Molodensky 方式では、実際に XYZ 系に変換することなく、2 つの地理座標系の間で変換が直接実行されます。Molodensky 方式を使用する場合は、3 つのシフト(dx,dy,dz)の他に、2 つの回転楕円体における長半径の差(Δa)と扁平率の差(Δf)も必要となります。投影エンジンにより、関連する測地基準に応じて楕円体の差が自動的に算出されます。
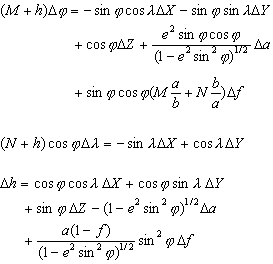
- h = 楕円体の高さ(メートル)
- Φ = 緯度
- λ = 経度
- a = 回転楕円体の長半径(メートル)
- b = 回転楕円体の短半径(メートル)
- f = 回転楕円体の扁平率
- e = 回転楕円体の偏心率
M と N は 、それぞれ特定の緯度における経線と本初子午線の曲率半径になります。M と N の数式は以下のとおりです。
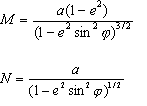
ΔλとΔΦの数式を解きます。解かれた値は、投影エンジンによって自動的に追加されます。
Abridged Molodensky変換
Abridged Molodensky 変換は、Molodensky 変換を簡略化したバージョンです。次の数式を参照してください。