サマリー
フィーチャまたはフィーチャに関連付けられた値が、ある範囲の距離について統計的に有意なクラスタリングまたは分散を示すかどうかを決定します。
[Ripley の K 関数法 (Multi-Distance Spatial Cluster Analysis (Ripleys K Function))] ツールの詳細
図
使用法
このツールで距離を正確に測定するには、投影データが必要です。
ツールの出力は、期待される K 値と観測された K 値をそれぞれ含む ExpectedK フィールドと ObservedK フィールドを持つテーブルです。L(d) 変換 が適用されるため、ExpectedK 値は常に距離値と一致します。DiffK という名前のフィールドは、観測された K 値から期待される K 値を引いた値を含みます。信頼区間のオプションを指定した場合は、LwConfEnv および HiConfEnv という 2 つのフィールドが出力テーブルに追加されます。これらのフィールドには、[距離バンド数] パラメーターで指定したツールの繰り返し実行ごとの信頼区間情報が格納されます。K 関数は、オプションとして、結果をまとめたグラフ レイヤーを作成します。
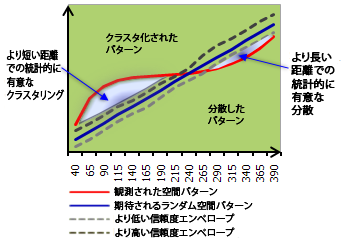
特定の距離で観測された K 値が期待される K 値より大きい場合、その距離 (分析のスケール) におけるランダム分布よりクラスタリングされた分布になります。観測された K 値が期待される K 値より小さい場合、その距離におけるランダム分布より分散された分布になります。観測された K 値が HiConfEnv 値より大きい場合、その距離の空間クラスター化は統計的に有意です。観測された K 値が LwConfEnv 値より小さい場合、その距離の空間分散は統計的に有意です。解釈の詳細については、「[Ripley の K 関数法 (Multi-Distance Spatial Cluster Analysis (Ripleys K Function))] の詳細 」をご参照ください。
[出力結果をグラフィックスで表示] パラメーターを有効にすると、ツールの結果をまとめた線グラフが作成されます。期待される結果は青い線で、観測された結果は赤い線で表されます。期待される線より上に観測された線がずれていると、その距離でデータセットがクラスタリングしていることを示します。期待される線より下に観測された線がずれていると、その距離でデータセットが分散していることを示します。線グラフはグラフ レイヤーとして作成されます。グラフ レイヤーは一時的で、ArcMap を閉じると削除されます。グラフ レイヤーを右クリックして [保存] をクリックすると、グラフがグラフ ファイルに書き込まれます。グラフを保存した後でマップ ドキュメントを保存すると、グラフ ファイルへのリンクが *.mxd ファイルに保存されます。グラフ ファイルの詳細については、「グラフによるデータの閲覧と視覚化」をご参照ください。
-
ライン フィーチャとポリゴン フィーチャの場合は、距離の計算にフィーチャの重心が使用されます。マルチポイント、ポリライン、または複数のパートを持つポリゴンの場合は、すべてのフィーチャ パートの加重平均中心を使用して重心が計算されます。加重は、ポイント フィーチャの場合は 1、ライン フィーチャの場合は長さ、ポリゴン フィーチャの場合は面積です。
[加重フィールド] は、それがインシデント数または件数を表すときに最も適切に使用されます。
[加重フィールド] を指定しなかった場合、最大の DiffK 値は、クラスター化を推進する空間プロセスが最も顕著な距離を示します。
以下に、信頼度エンベロープの計算方法を説明します。
- [加重フィールド] の指定なし
[加重フィールド] を指定しなかった場合、信頼度エンベロープは、分析範囲にポイントをランダムに配置して、その分布の L(d) 値を計算することで作成されます。ポイントのランダム分布はそれぞれ「順列」と呼ばれます。たとえば 99_PERMUTATIONS を選択した場合、ポイント集合は繰り返し実行ごとに 99 回ランダムに配置されます。ポイント集合が 99 回配置された後、距離ごとに、期待される K 値より上下に最も大きくずれた、観測された K 値が選択されます。これらの値が信頼区間になります。
- [加重フィールド] の指定あり
[加重フィールド] を指定した場合は、ウェイト値だけがランダムに再配置されて、信頼度エンベロープが計算されます。ポイント位置は固定です。基本的に、[加重フィールド] を指定した場合、位置は固定されたままで、空間におけるフィーチャ値のクラスタリングが評価されます。一方、[加重フィールド] を指定しなかった場合は、フィーチャ位置のクラスタリングまたは分散が分析されます。
- [加重フィールド] の指定なし
信頼度エンベロープ はランダムな順列から作成されるため、たとえパラメーターが同一であっても、信頼度エンベロープを定義する値は実行ごとに変化します。ただし、乱数ジェネレーター ジオプロセシング環境用のシード値を設定した場合は、繰り返し分析でも一貫した結果が生成されます。
[信頼度エンベロープの計算] パラメーターで選択した順列数と信頼度の関係は、おおまかに 9 は 90%、99 は 99%、999 は 99.9% と考えることができます。
分析範囲を指定しないと、分析範囲ポリゴンとして最小限の領域を囲む四角形が使用されます。範囲とは違って、最小限の領域を囲む四角形は必ずしも X 軸、Y 軸と並行ではありません。
K 関数統計は、分析範囲のサイズに対して非常に敏感です。ポイントの配置が同じでも、それを囲む分析範囲のサイズによってクラスタリングされたり分散されたりすることがあります。そのため、分析範囲の境界を慎重に検討することが必須です。下図は、同一のフィーチャ分布でも、指定された分析範囲によって分散されたりクラスタリングされたりする典型的な例です。
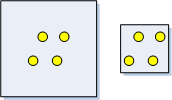
[分析範囲の指定方法] パラメーターで USER_PROVIDED_STUDY_AREA_FEATURE_CLASS を選択した場合は、分析範囲フィーチャクラスが必要です。
[分析範囲のフィーチャクラス] を指定した場合、そのフィーチャクラスは正確に 1 つのシングル パート フィーチャ (分析範囲ポリゴン) を持つ必要があります。
[開始距離] または [距離の増分] を指定しなかった場合、入力フィーチャクラスの範囲に基づいてデフォルト値が計算されます。
K 関数には、分析範囲の境界近くにあるフィーチャの数を実際より少なく数えるというバイアスがあります。[分析境界付近の補正方法] パラメーターで、このバイアスに対処する方法を指定できます。
- NONE
特定の補正方法を適用しません。ただし、入力フィーチャクラスのポイントのうち、ユーザーが指定した分析範囲の外側にくるものは、近傍カウント時に使用されます。この方法が適切なのは、非常に大きな分析範囲からデータを収集していて、データ コレクションの境界内におさまる小さなエリアを分析するだけでいい場合です。
- SIMULATE_OUTER_BOUNDARY_VALUES
この方法は、分析範囲の境界の内側にあるポイントの鏡像となるポイントを境界の外側に作成して、エッジ近くの過小推計を補正します。分析範囲のエッジの最大距離バンド以内の距離にあるポイントがコピーされます。コピーされたポイントは、エッジ ポイントの近傍推計が正確になるように使用されます。下図は、計算時にどのポイントが使用され、どのポイントがエッジ補正だけに使用されるかを示しています。
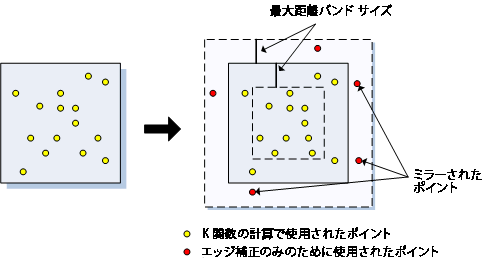
- REDUCE_ANALYSIS_AREA
このエッジ補正方法は、分析で使用する最大距離バンドと等しい距離だけ、分析範囲のサイズを縮小します。分析範囲の縮小後は、新しい分析範囲の外側にあるポイントは、まだ分析範囲内にあるポイントの近傍カウントが評価されるときだけ考慮されます。K 関数の計算時には、他の形では使用されません。下図は、計算時にどのポイントが使用され、どのポイントがエッジ補正だけに使用されるかを示しています。
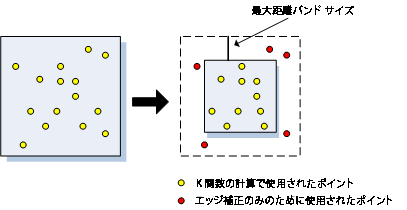
- RIPLEY'S_EDGE_CORRECTION_FORMULA
この方法は、ポイントごとに、分析範囲のエッジからの距離と、近傍ポイントそれぞれとの距離を確認します。分析範囲のエッジからの距離よりも離れている近傍ポイントにはすべて、追加のウェイトがかけられます。このエッジ補正方法が適切なのは、分析範囲が正方形または長方形の場合、または、[分析範囲の指定方法] パラメーターで MINIMUM_ENCLOSING_RECTANGLE を選択した場合だけです。
- NONE
分析境界付近の補正を適用しないと、分析距離が増えるにしたがって実際より少なく数えるバイアスが増えます。[出力結果をグラフィックスで表示] パラメーターを有効にすると、観測された K 値のラインが大きな距離で垂れ下がります。
数学的には、[Ripley の K 関数法 (Multi-Distance Spatial Cluster Analysis (Ripleys K Function))] ツールは、ランダムなポイント集合の期待される結果が入力距離に等しい Ripley の K 関数の共通変換を使用します。変換 L(d) を以下に示します。
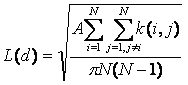
ここで、A は面積、N はポイント数、d は距離、k(i, j) はウェイトです。ウェイトは、境界付近の補正がない場合、i と j の距離が d 以下のときは 1、i と j の距離が d より大きいときは 0 です。エッジ補正がある場合、k(i,j) のウェイトは少し修正されます。
-
マップ レイヤーを使用して、入力フィーチャクラスを指定できます。解析対象として指定したレイヤーの中で何らかのフィーチャが選択されている場合、選択されているフィーチャだけが解析の対象となります。
構文
MultiDistanceSpatialClustering_stats (Input_Feature_Class, Output_Table, Number_of_Distance_Bands, {Compute_Confidence_Envelope}, {Display_Results_Graphically}, {Weight_Field}, {Beginning_Distance}, {Distance_Increment}, {Boundary_Correction_Method}, {Study_Area_Method}, {Study_Area_Feature_Class})| パラメーター | 説明 | データ タイプ |
Input_Feature_Class | 分析対象となるフィーチャクラスです。 | Feature Layer |
Output_Table | 分析結果が書き込まれるテーブルです。 | Table |
Number_of_Distance_Bands | 近傍サイズを増やしてデータセットのクラスタリングを分析する回数です。開始ポイントと増やすサイズは、それぞれ Beginning_Distance パラメーターと Distance_Increment パラメーターで指定します。 | Long |
Compute_Confidence_Envelope (オプション) | 信頼度エンベロープは、分析範囲にフィーチャ ポイント (またはフィーチャ値) をランダムに配置して計算されます。ランダムに配置するポイントまたは値の数は、フィーチャクラス内のポイントの数と等しくなります。ランダム配置の各組は順列と呼ばれ、この順列から信頼度エンベロープが作成されます。このパラメーターでは、信頼度エンベロープを作成するときに使用する順列の数を指定できます。
| String |
Display_Results_Graphically (オプション) | 結果をまとめたグラフ レイヤーを作成するかどうかを指定します。
| Boolean |
Weight_Field (オプション) | 各位置のフィーチャ数またはイベント数を表すウェイトが格納された数値フィールドです。 | Field |
Beginning_Distance (オプション) | クラスター分析を開始する距離で、ここを起点として距離が増やされます。このパラメーターの値は、出力座標系の単位で入力する必要があります。 | Double |
Distance_Increment (オプション) | 繰り返し実行ごとに増やす距離です。分析で使用する距離は Beginning_Distance で指定した距離から始まり、Distance_Incrementで指定した値だけ増やされます。このパラメーターの値は、[出力座標系] 環境設定の単位で入力する必要があります。 | Double |
Boundary_Correction_Method (オプション) | 分析範囲のエッジ近くにあるフィーチャの近傍数が実際よりも少なく推計されるのを補正する方法です。
| String |
Study_Area_Method (オプション) | 分析範囲として使用する領域を指定します。K 関数は、分析範囲のサイズの変更に対して敏感です。この値は慎重に選択する必要があります。
| String |
Study_Area_Feature_Class (オプション) | 入力フィーチャクラスを分析するエリアを定義するフィーチャクラスです。Study_Area_Method = "USER_PROVIDED_STUDY_AREA_FEATURE_CLASS" の場合にのみ指定します。 | Feature Layer |
コードのサンプル
Multi-DistanceSpatialClusterAnalysis (Ripley の K 関数法) の例 (Python ウィンドウ)
次の Python ウィンドウ スクリプトは Multi-DistanceSpatialClusterAnalysis (Ripley の K 関数法) ツールを使用する方法を示しています。
import arcpy
arcpy.env.workspace = r"C:\data"
arcpy.MultiDistanceSpatialClustering_stats("911Calls.shp","kFunResult.dbf", 11,
"0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE",
"NO_DISPLAY", "#", 1000, 200,"REDUCE_ANALYSIS_AREA",
"MINIMUM_ENCLOSING_RECTANGLE", "#")
Multi-DistanceSpatialClusterAnalysis (Ripley の K 関数法) の例 (スタンドアロン Python スクリプト)
次のスタンドアロン Python スクリプトは Multi-DistanceSpatialClusterAnalysis (Ripley の K 関数法) ツールを使用する方法を示しています。
# Use Ripley's K-Function to analyze the spatial distribution of 911
# calls in Portland Oregon
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# Set Distance Band Parameters: Analyze clustering of 911 calls from
# 1000 to 3000 feet by 200 foot increments
numDistances = 11
startDistance = 1000.0
increment = 200.0
# Process: Run K-Function...
kFun = arcpy.MultiDistanceSpatialClustering_stats("911Calls.shp",
"kFunResult.dbf", numDistances,
"0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE",
"NO_DISPLAY", "#", startDistance, increment,
"REDUCE_ANALYSIS_AREA",
"MINIMUM_ENCLOSING_RECTANGLE", "#")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
環境
ライセンス情報
- ArcGIS Desktop Basic: はい
- ArcGIS Desktop Standard: はい
- ArcGIS Desktop Advanced: はい