ArcMap

傾斜方向 (Aspect) の仕組み

Spatial Analyst のライセンスで利用可能。

3D Analyst のライセンスで利用可能。

[傾斜方向 (Aspect)] ツールは、下りの傾斜角が指している方向を特定します。出力ラスターの各セルの値は、その位置でサーフェスが向いている方位方向を示しています。傾斜方向は、0 度 (真北) ～ 360 度 (真北) で右回りに計測されます。下り方向のない平坦な領域には -1 という値が割り当てられます。

傾斜方向
傾斜方向

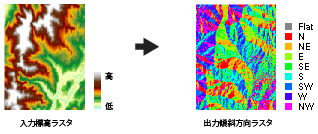
以下の図に、入力標高データセットと出力傾斜方向ラスターを示します。

傾斜方向の出力例

傾斜方向 (Aspect) ツールを使用する目的

[傾斜方向 (Aspect)] ツールでは、次の操作を行えます。

  • スキーに最適な斜面を検索する際に、ある山の北側斜面をすべて検出する。
  • 各地の生活の多様性を調べる研究の一環として、ある地域の各場所における直射日光照度を計算する。
  • 雪解け水が最初に流れ込む可能性がある住宅地域を特定する研究の一環として、山岳地域の南に面する傾斜のうち、雪が最初に融ける場所を検出する。
  • 緊急時に航空機が着陸できる平坦地を特定する。

計算方法とエッジ効果

傾斜方向を計算する方法は 2 つあります。[方法] パラメーターを使用して [平面] 計算を実行するか、[測地線] 計算を実行するかを選択できます。

平面方法では、二次元の直交座標系を使用し、投影された平面上で計算が実行されます。測地線方法では、地球の形を楕円体と見なすことで三次元の直交座標系で計算が実行されます。

平面計算と測地線計算のいずれもが、3 セル X 3 セルの近傍 (移動する枠) の使用によって実行されます。各近傍で、処理 (中央の) セルが NoData の場合、出力は NoData になります。また、計算を実行するには、処理セルに隣接しているセルのうち、少なくとも 7 つのセルが有効な値を保持している必要があります。有効なセルの数が 7 未満である場合、計算は実行されず、その処理セルの出力は NoData になります。

出力ラスターの最も外側のロウとカラムにあるセルは NoData になります。これは、これらのセルが、入力データセットの境界沿いにあり、必要なだけの有効な隣接セルに囲まれていないためです。

平面方法

平面方法は、傾斜方向を計算する従来の方法です。

平面上での傾斜方向のアルゴリズム

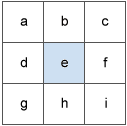
移動する 3 x 3 の枠が入力ラスターの各セルを巡り、枠の中央にある各セルについて、そのセルの 8 個の近傍セルの値を加味したアルゴリズムを使用して傾斜方向の値が計算されます。これらのセルは a ～ i の文字で識別され、傾斜方向の計算対象となるセルには e が割り当てられます。

サーフェス枠
サーフェス枠

セル e の X 方向の変化率は、次のアルゴリズムで計算されます。

  [dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8
  • ここで、

    wght1 と wght2 は有効なセルの水平加重計数値です。

    次に例を示します。

    • c、f、および i の値がすべて有効な場合は、wght1 = (1+2*1+1) = 4 になります。
    • i が NoData の場合は、wght1 = (1+2*1+0) = 3 になります。
    • f が NoData の場合は、wght1 = (1+2*0+1) = 2 になります。

    隣接位置が a、d、g である場合を除き、同じようなロジックが wght2 にも適用されます。

セル e の Y 方向の変化率は、次のアルゴリズムで計算されます。

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4 ) / 8
  • ここで、

    wght3 と wght4 は [dz/dx] の計算で見られたものと同じ概念を表しています。

セル e の X 方向と Y 方向の両方の変化率を考慮して、傾斜方向は次のように計算されます。

  aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx])

傾斜方向の値は、次の規則に従って、コンパス方向の値 (0 ～ 360 度) に変換されます。 

  if aspect < 0    cell = 90.0 - aspect>
  else if aspect > 90.0    cell = 360.0 - aspect + 90.0  else    cell = 90.0 - aspect

平面上での傾斜方向の計算例

例として、移動する枠の中央セルについて、平面上での傾斜方向値を計算します。

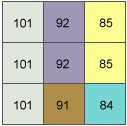
傾斜方向の計算例の入力
傾斜方向の計算例の入力

中央セル e の X 方向の変化率は、次のように計算されます。 

  [dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8          = ((85 + 170 + 84)*4/(1+2+1) - (101 + 202 + 101)*4/(1+2+1)) / 8          = -8.125

中央セル e の Y 方向の変化率は、次のように計算されます。 

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / 8          = ((101 + 182 + 84)*4/(1+2+1) - (101 + 184 + 85)*4/(1+2+1)) / 8          = -0.375

傾斜方向は、次のように計算されます。 

  aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx])         = 57.29578 * atan2 (-0.375, 8.125)         = -2.64

計算された値がゼロより小さいため、最終ルールが次のように適用されます。 

  cell = 90.0 - aspect       = 90 - (-2.64)       = 90 + 2.64       = 92.64

中央セル e の 92.64 という値は、その傾斜方向が東方向であることを示しています。

平面上での傾斜方向計算例の出力
平面上での傾斜方向計算例の出力

測地線方法

測地線方法では、地球の形を楕円体と見なすことで、地心三次元座標系 (Earth Centered、Earth Fixed (ECEF) 座標系とも呼ばれる) でのサーフェスの傾斜方向を計測します。データセットの投影方法は、この計算結果に影響しません。入力ラスターの Z 単位が空間参照で定義されている場合は、この単位が使用されます。入力の空間参照で Z 単位が定義されていない場合は、Z 単位パラメーターを使用して定義する必要があります。測地線方法では、平面方法と比べて、より精度の高い傾斜方向が得られます。

測地座標変換

ECEF 座標系は、地球の中心を原点とする三次元の右手直交座標系です。この座標系では、すべての位置が X、Y、Z 座標で表現されます。次の図は、地心座標により表された目標位置 T の例です。

ECEF 座標系
サーフェス ラスターは、入力座標系から地心三次元座標系に変換されます。

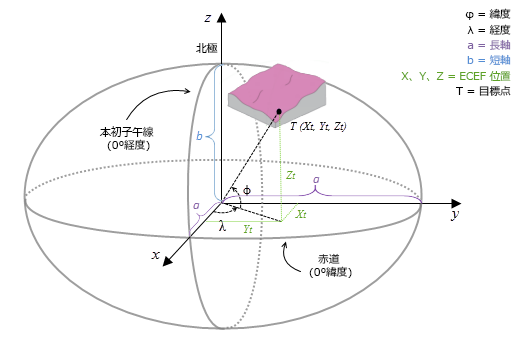
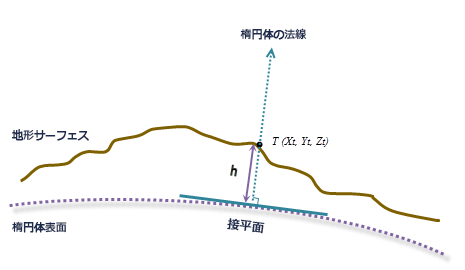
測地線計算では、測地座標 (緯度 φ、経度 λ、高度 h) に基づいて計算される X, Y, Z 座標を使用します。入力サーフェス ラスターの座標系が投影座標系 (PCS) である場合は、最初に、各位置に測地座標が含まれているラスターが地理座標系 (GCS) に再投影され、その次に ECEF 座標系に変換されます。高度 h (Z 値) は楕円形表面を基準とする楕円体の高さです。次の図をご参照ください。

楕円体の高さ
楕円体の高さ

ECEF 座標を測地座標 (緯度 φ、経度 λ、高度 h) に変換するには、次の式を使用します。

X = (N(φ)+h)cosφcosλ
Y = (N(φ)+h)cosφsinλ
Z = (b2/a2*N(φ)+h)sinφ
  • ここで、
    • N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
    • φ = 緯度
    • λ = 経度
    • h = 楕円体の高さ
    • a = 楕円体の長軸
    • b = 楕円体の短軸

上記の式で、楕円体の高さはメートル単位です。ご使用の入力ラスターの Z 単位がこれ以外の単位で指定されている場合は、内部的にメートルに変換されます。

傾斜方向の計算

ある位置における測地線傾斜方向は、楕円体表面に平行である平面上での、北を基準とした下り斜面の方向を表しています。

各位置の傾斜方向を計算するために、3 セル X 3 セルの近傍平面が、最小二乗法 (LSM) を使用して、各処理セルの周りでフィッティングされます。LSM による最適なフィットの位置では、実際の Z 値とフィッティング後の Z 値の差の二乗和 (SSD: Sum of Squared Differece) (dzi) が最小化されます。例については、下の図をご参照ください。

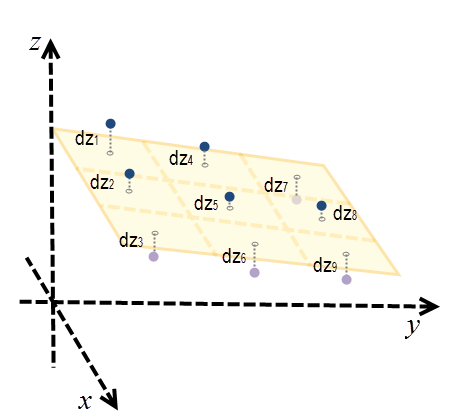
最小二乗フィッティングの例
最小二乗フィッティングの例

平面は z = Ax + By + C で表されます。各セルの中心で、dzi は実際の Z 値とフィッティング後の Z 値の差を示します。

∑9i=1dzi2 が最小になったときに平面が最適にフィッティングされます。

平面のフィッティング後、そのセルの位置でサーフェスの法線が計算されます。また、同じ位置で、楕円表面の接平面に垂直である楕円体の法線も計算されます。

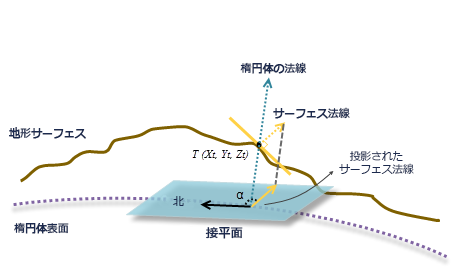
測地線傾斜方向の計算
測地線傾斜方向の計算

楕円体表面の接平面が参照平面と見なされるため、サーフェス法線が平面上に垂直に投影されます。最後に、サーフェス法線の垂直投影と北の間の時計回りの角度 α を計測することにより、測地線傾斜方向が計算されます (上図を参照)。

GPU の使用

測地線方法の場合、このツールは、特定の GPU ハードウェアをシステムにインストールしている場合に、パフォーマンスの向上が可能です。このツールをサポートする方法、構成する方法、および有効化する方法の詳細については「Spatial Analyst での GPU 処理」をご参照ください。

参照

Burrough, P. A., and McDonell, R. A., 1998. 『Principles of Geographical Information Systems』 (Oxford University Press, New York), 190 pp.

Marcin Ligas, and Piotr Banasik, 2011. 『Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations』 (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159

E.J.Krakiwsky、D.E.Wells 共著、1971、 『Coordinate Systems In Geodesy』 (GEODESY AND GEOMATICS ENGINEERING、UNB)、LECTURE NOTES、No16、1971、pp. 18-38。

Lancaster, P、Šalkauskas, K. 共著、 『Curve and Surface Fitting: An Introduction.』 London: Academic Press、1986。

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. 『GPS - theory and practice.』 Section 10.2.1. p. 282.

David Eberly 1999. 『Least Squares Fitting of Data』 (Geometric Tools, LLC), pp. 3.

関連トピック