Доступно с лицензией Geostatistical Analyst.
Интерполяция по методу глобального полинома согласовывает полином со всей поверхностью, а интерполяция по методу локальных полиномов подбирает множество полиномов, каждый из которых подбирается к определенной перекрывающейся окрестности. Окрестность поиска может быть определена размером и формой, числом соседей и конфигурацией сектора.. Или с помощью параметра Исследовательского анализа поверхности тренда (Exploratory Trend Surface Analysis) можно одновременно изменять значения параметров Ширина полосы (Bandwidth), Пространственное число обусловленности (Spatial Condition Number) (при наличии) и Окрестность поиска (Searching Neighborhood).
Оптимизация параметров 9Parameter optimization), которая основана на статистике перекрестной проверки, можно также выполнить для LPI с помощью кнопки Оптимизировать (Optimize ) 
.
Глобальный полином первого порядка соответствует прямой плоскости, проходящей через данные; глобальный полином второго порядка соответствует поверхности с изгибом, позволяя отображать долины; глобальный полином третьего порядка может характеризовать два изгиба и т. п. Но для поверхности с меняющейся формой, например, ландшафта с чередованием склонов и ровных поверхностей, глобальный полином не подходит. Сложные полиномиальные плоскости представят поверхность более точно, как показано на рисунке ниже):
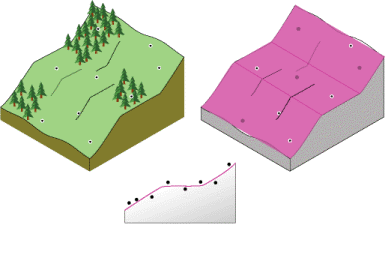
С другой стороны, интерполяция по методу локальных полиномов подходит для заданного порядка (нулевой, первый, второй, третий и т. д.) полинома, использующего только точки в определенной окрестности. Окрестности перекрываются, а значение, используемое для каждого проинтерполированного значения, является значением подобранного полинома в центре окрестности.
На следующем рисунке показано поперечное сечение данных высот (разрез). На первом рисунке три соседа (красные точки) используются для подбора полинома первого порядка, а красная линия – для интерполяции неизвестного значения для местоположения, обозначенного синей точкой. На втором рисунке второе местоположение (желтая точка) прогнозируется с помощью другого полинома первого порядка. Это положение находится рядом с первым местоположением, а в интерполяции используются те же самые измеренные точки, но веса будут немного различаться, следовательно, подбор полинома (синяя линия) будет немного отличаться.
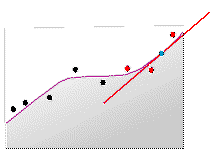
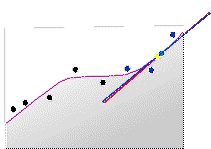
Процесс продолжается, выполняется центририрование на последовательных местоположениях интерполяции и подбор локальных полиномов для интерполяции значений. На следующих двух рисунках представлены две случайные интерполируемые точки для создания результирующей поверхности. Оранжевая точка проинтерполирована из подобранного полинома (зеленая линия) с помощью зеленых измеренных опорных точек, а коричневая точка проинтерполирована из светло-фиолетового полинома.
На следующих двух рисунках еще два полинома (желтая и серая линии) интерполируют еще два местоположения (голубовато-зеленая и зеленая точки).
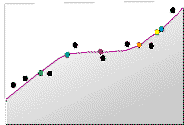
Данный процесс продолжается для каждого местоположения. Можно отследить создание поверхности (фиолетовая линия поверхности) для опорных точек, представленных ниже.
Оптимальные параметры выбираются для того, чтобы минимизировать среднеквадратическую ошибку интерполяции (RMSPE), подобно выбору значения степени (p) в методе IDW.
Меры точности
Интерполяция по методу локальных полиномов предоставляет две меры точности, недоступные для других детерминированных методов интерполяции в ArcGIS Geostatistical Analyst:
- Стандартные ошибки интерполяции показывают неопределенность, связанную с проинтерполированным значением, для каждого местоположения.
- Пространственное число обусловенности является мерой стабильности или нестабильности решения уравнений интерполяции для конкретного положения. Если число обусловленности велико, небольшое изменение коэффициентов матрицы приведет к существенному изменению в векторе решения (коэффициентах регрессии). Поверхность пространственного числа обусловленности демонстрирует изменение в стабильности числовой модели и предоставляет дополнительную информацию по неопределенности интерполяции, так как поверхность стандартной ошибки интерполяции создается с учетом того, что модель верна.
Интерполяция по методу локальных полиномов опирается на следующие допущения:
- Образцы были отобраны по регулярной сетке, то есть через равные расстояния.
- Значения данных в окрестности поиска нормально распределены.
На практике большинство наборов данных не соответствуют этим допущениям. В таком случае затрагиваются интерполируемые значения, но не так сильно, как стандартные ошибки интерполяции. Чтобы понять, достоверны результаты в определенной области или нет, LPI предоставляет поверхность пространственного числа обусловленности. В следующей таблице представлено правило эмпирических значений, а критические значения отображены желтым на поверхности Пространственного числа обусловленности:
| Порядок полинома | Критическое пороговое значение пространственного числа обусловленности |
|---|---|
1 | 10 |
2 | 100 |
3 | 1000 |
Больше 3 | Не рекомендуется в большинстве ситуаций |
Значения ниже критического порога пространственного числа обусловленности указывают на местоположения, в которых решения достоверны. Значения, близкие или равные критическим значениям, маловероятны (должны быть тщательно исследованы), а значения выше критических пределов недостоверны.
Пространственные числа обусловленности выводится оцениванием того, насколько чувствительны прогнозируемые значения к небольшим изменениям коэффициентов линейных уравнений интерполяции. Небольшие пространственные числа обусловленности указывают на то, что решение стабильно, тогда как большие значения говорят о том, что решение нестабильно. Отсутствие стабильности решения должно обеспокоить, если такое решение возникает в областях особого интереса, поскольку небольшие изменения входных данных (включая их значения, положения и пространственное расположение) могут привести к значительному изменению интерполируемого значения. Это значит, что любая неопределенность, связанная со входными данными (например, ошибки в измерениях атрибутов или неточности в координатах, где были выполнены измерения), и в особенности, выпадающие значения в данных могут оказывать значительное влияние на проинтерполированные значения. Изменения в окрестности поиска также изменяют количество точек данных (и веса в случае сглаженной окрестности поиска), которые используются для выполнения интерполяции, и могут оказывать влияние на пространственное число обусловленности для этого местоположения.
Поверхность пространственного числа обусловленности создана для полиномов первого, второго и третьего порядка. Стандартная ошибка интерполяции оценена при допущении, что модель LPI верна (то есть регрессия по методу наименьших квадратов является достоверным алгоритмом, и значения пространственного числа обусловленности меньше, чем пороговые значения пространственного числа обусловленности в таблице, приведенной выше).
Можно исключить области, в которых случаются высокие значения числа обусловленности, на картах проинтерполированных значений и картах стандартных ошибок интерполяции, путем определения параметра Использовать порог пространственного числа обусловленности (Use Spatial Condition Number Threshold) как Истина (True) в диалоговом окне LPI. Число обусловленности зависит только от местоположений входных точек, а не их текущих значений. Другими словами, используются ли значение концентрации озона или значения высоты из одного набора данных в качестве входных данных для метода LPI, поверхность числа обусловленности будет одинаковой.
В случае равномерно распределенных данных, ядра Константа (Constant), Епанечникова (Epanechnikov) и Четвертого порядка (Quartic) будут лучшими с теоретической точки зрения для полиномов нулевого, первого и второго порядка соответственно. В случае неравномерно распределенных данных, выбор лучшего ядра должен основываться на диагностике проверки и перекрестной проверки и значениях пространственного числа обусловленности.
Интерполяция ядра с барьерами (Kernel Interpolation with Barriers) – вариант LPI. Локальная нестабильность в этих результатах корректируется с помощью метода, схожего с гребневой регрессией. С другой стороны, проинтерполированные значения слегка смещены и в большинстве практических ситуаций такое смещение не оказывает сильного влияния на решения, принимаемые на основе проинтерполированных значений.
Пробелы поверхности
Значения у параметров Ширина полосы (Bandwidth), Пространственное число обусловленности (Spatial Condition Number) и Окрестность поиска (Searching Neighborhood), как правило, изменяются с помощью кнопки Оптимизировать (Optimize) 
. Если параметр Порог чисел пространственных условий установлен в значение Ложь (False), то изменить можно будет только значения Ширина полосы и Окрестность. Если для параметра Тип окрестности установлено значение Стандартная, то используются все данные, но не более 1000 точек, а минимальное число соседей устанавливается равным нулю. Оптимизация выполняется для типа Сектор (Sector), равного 1 Сектор, и для сглаженной окрестности. Такой процесс оптимизации может привести к «дырам» в выходной поверхности. Существуют области, на которых превышен Порог пространственного числа обусловленности (Spatial Condition Number Threshold) или окрестность поиска слишком мала. Параметры окрестности поиска и порога пространственного числа обусловленности можно подобрать, чтобы заполнить эти области; но необходимо отметить, что дыры возникают там, где может наблюдаться нестабильность в вычислении интерполируемых значений.
Когда используется интерполяция по методу локальных полиномов
Интерполяция по методу глобального полинома полезна для создания сглаженных поверхностей и определения трендов в наборе данных, характерных для всей территории исследования. Однако в науках о Земле переменная интереса обычно имеет вариацию для малых диапазонов наряду с трендом для всей территории. Если в наборе данных есть вариация для малых диапазонов, ее можно обнаружить с помощью инструмента Интерполяция по методу локальных полиномов (Local Polynomial Interpolation).
Интерполяция по методу локальных полиномов чувствительна к размеру окрестности, а небольшие окрестности поиска могут на интерполируемой поверхности создать пустые области. Поэтому необходимо просмотреть поверхность перед созданием выходного слоя.