Понятие ординарного кригинга

Доступно с лицензией Geostatistical Analyst.

Ординарный кригинг предполагает модель,

Z(s) = µ + ε(s),

где µ является неизвестной константой. Один из основных вопросов, касающихся ординарного кригинга, обоснованно ли допущение постоянного среднего значения. В отдельных случаях есть веские научные обоснования для отклонения этого допущения. Однако в качестве простого метода интерполяции он обладает выдающейся гибкостью. На приведенном ниже рисунке показан пример в одном пространственном измерении:

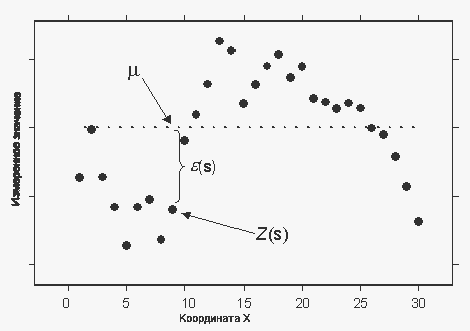
По-видимому, данные — это значения высот, полученных на линии профиля, проходящего через долину и гору. Также очевидно, что данные более непостоянны слева и сглаживаются ближе к правой стороне. На самом деле, эти данные были смоделированы с помощью модели ординарного кригинга с постоянным средним значением µ. Истинное, но неизвестное значение дано пунктирной линией. Следовательно, ординарный кригинг можно использовать для данных, которые предположительно имеют тренд. Основываясь лишь на данных, невозможно решить, является ли наблюдаемый шаблон результатом автокорреляции (наряду с ошибками ε(s) с константой или тренда, где µ(s) изменяется с s).

Ординарный кригинг может использовать вариограммы либо ковариации (математические формы, используемые для выражения автокорреляции), применять преобразования и удалять тренды, а также учитывать погрешность измерения.

Отзыв по этому разделу?