Инструмент Медианный центр измеряет центральную тенденцию, которая устойчива к выбросам. Идентифицирует местоположение, минимизирующее путь до всех других пространственных объектов в наборе данных. Например, если вам надо рассчитать Усредненный Центр (Mean Center) для компактного кластера точек, результатом будет расположение в центре кластера. Если вы потом добавите точку далеко от кластера и пересчитаете Усредненный Центр (Mean Center) , вы заметите, что результат будет смещен к новому выбросу. Если тот же самый эксперимент выполнить с инструментом Медианный Центр (Median Center) , вы бы увидели, что новый выброс оказывает значительно меньшее влияние на результат. Инструмент Медианный Центр (Median Center) позволяет указывать Поле веса (Weight Field). Можно представить веса как количество поездок, связанных с каждым объектом (например, если вес для объекта - 3,2, количество поездок будет 3,2). Взвешенный медианный центр - местоположение, минимизирующее расстояние для всех поездок.
Метод, используемый для расчета Медианного центра (Median Center), — это итерационная процедура, предложенная в [Kuhn, Kuenne, 1962] и получившая развитие в [Burt, Barber, 1996]. На каждом шаге алгоритма (t) находится кандидат на Медианный центр (Median Center) (Xt, Yt), который затем уточняется до тех пор, пока он не будет представлять положение, минимизирующее Эвклидово расстояние d до всех объектов (или всех взвешенных объектов) (i) в наборе данных.
Вычисления
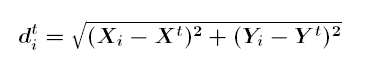
Результат
Инструмент Медианный центр (Median Center) создает новый Выходной класс объектов (Output Feature Class) с одним точечным объектом, соответствующем медианному центру, или для каждого случая, когда указано Поле комбинаций (Case Field). Координаты Х и Y медианного центра, медианные значения поля комбинаций и атрибутивного поля (одно поле для каждого Атрибутивного поля (Attribute Field) ) являются атрибутами в выходном классе объектов. Значение каждого Атрибутивного поля (Attribute Field) является вычисленным медианным значением для всех значений поля. Медианное значение для набора чисел — это срединное значение: половина значений в наборе данных меньше его, а другая половина — больше.
Возможные приложения
Инструмент Медианный центр (Median Center) можно использовать для измерения центральной тенденции, которая устойчива к пространственным выбросам. Вы можете использовать этот инструмент для расчетов медианного центра пожаров, когда необходимо исключить влияние редких периферийных случаев пожаров на определение центра пожарной опасности. Как правило, интересно сравнивать результаты Среднего центра (Mean Center) и Медианного центра (Median Center) , чтобы оценить влияние периферийных объектов на результаты. Для многих приложений, Медианный Центр является более репрезентативной мерой центральной тенденции, чем Средний Центр.
Дополнительные ресурсы
Следующие книги содержат детальную информацию по этому инструменту:
Берт Дж. И. (Burt, J. E.), Барбер Дж. (G. Barber). (1996). Элементарная статистика для географов. Guilford, New York.
Кун Х.В. (Kuhn, H. W.), Кюнне Р.Э. (R. E. Kuenne) (1962). Эффективны алгоритм для числовых решений Generalized Weber Problem в пространственной экономике. Journal of Regional Science, 4(2):21–33.