Доступно с лицензией Geostatistical Analyst.
В разделе Анализ свойств поверхности в соседних точках была представлена интерполяция, которая зависит от расстояния. Существуют и другие решения для прогнозирования значений для неизмеренных местоположений. Другим предложенным местом для наблюдения является склон пологого холма. Склон холма представляет собой наклонную плоскость. Однако опорные точки измерялись в небольших углублениях или на небольших бугорках (локальная вариация). Использование соседних точек для интерполяции местоположения может давать завышенную или заниженную оценку из-за влияния углублений и бугорков. Кроме того, можно натолкнуться на локальную вариацию и неправильно оценить общий наклон плоскости (который называется трендом). Способность идентифицировать и моделировать локальные структуры и тренды поверхностей может повысить точность интерполированной поверхности.
Интерполяция по методу глобального полинома
Чтобы интерполяция базировалась на превалирующем тренде, можно подобрать плоскость между опорными точками. Плоскость — это особое семейство математических формул, которые называются полиномами. Затем можно определить неизвестную высоту для интерполируемого местоположения на основании значения на плоскости. Плоскость может оказаться выше одних точек и ниже других. Задачей интерполяции является сведение ошибок к минимуму. Чтобы измерить ошибку, нужно вычесть значение для каждой измеренной точки из проинтерполированного значения на плоскости, возвести его в квадрат и добавить к общей сумме таких результатов. Такая сумма называется подбором по методу наименьших квадратов. Этот процесс является теоретической базой для интерполяции по методу глобального полинома первого порядка.
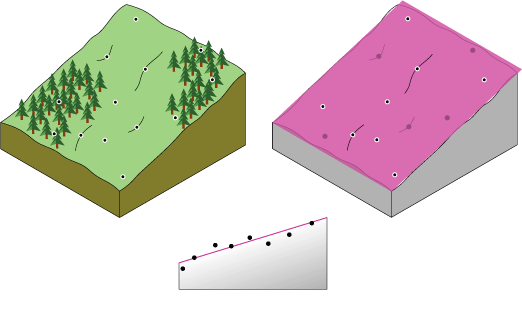
Но что произойдет, если попытаться подобрать плоскость к ландшафту с долиной? Получить хорошую поверхность из плоскости будет затруднительно. Однако если в плоскости разрешен один изгиб, возможно, подбор окажется более подходящим (ближе к большему числу значений). Допуск одного изгиба является базой для интерполяции по методу глобального полинома второго порядка (см. ниже). Два изгиба в плоскости можно описать полиномом третьего порядка и т. д. Изгибы могут возникать в обоих направлениях, и в результате поверхность может принять форму чаши.
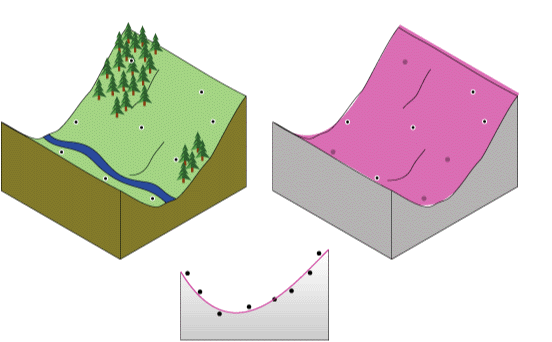
Общие сведения о работе интерполяции по методу глобального полинома