Доступно с лицензией Geostatistical Analyst.
Во многих геоинформационных источниках под площадной интерполяцией понимается непосредственно перераспределение данных из одного набора полигонов (полигоны-источники) в другой (целевые полигоны). К примеру, исследователям в области демографии часто требуется представлять демографические данные в разных единицах территориального деления. Если имеются данные о численности населения на уровне административных областей, исследователям может потребоваться пересчитать эти данные, чтобы оценить численность населения для территорий меньшей площади. В случае распределения данных по полигонам малой площади, может потребоваться интерполяция значений для образования совершенно отличного набора полигонов.
Площадная интерполяция (areal interpolation) в дополнительном модуле ArcGIS Geostatistical Analyst extension является геостатистическим методом интерполяции, в основе которого лежит теория кригинга (kriging), применяемая в отношении данных, усредненных или агрегированных по полигонам. Для всех точек, лежащих внутри этих полигонов и между ними, могут быть вычислены значения интерполяции и их среднеквадратические ошибки, а затем эти значения (вместе с ошибками) могут быть повторно агрегированы в новый набор полигонов.
Другие методы на основе кригинга, используемые Geostatistical Analyst, работают только с непрерывными точечными данными, имеющими нормальное (Гауссово) распределение, но метод интерполяции по площади может применяться к полигональным данным с дискретными значениями. Кроме того, может использоваться второй набор полигонов в качестве переменной кокригинга (cokriging); эти второстепенные полигоны могут иметь ту же геометрию, что и полигоны главной переменной, или же совершенно отличаться от них.
Ход работы для повторного агрегирования данных из полигонов в полигоны
Процесс повторного агрегирования данных (к примеру, пересчет данных о численности населения) состоит из двух этапов. В первую очередь на основе полигонов-источников создается сглаженная поверхность значений интерполяции (часто эта поверхность может рассматриваться как график плотности или вероятности), затем эта поверхность интерполяции подвергается повторному агрегированию в целевые полигоны. Создание такой поверхности требует применения методов вариографии в интерактивном режиме, поэтому производится в Мастере операций геостатистики (Geostatistical Wizard). Результатом работы Мастера операций геостатистики (Geostatistical Wizard) является геостатистический слой интерполяции или стандартных ошибок интерполяции. Если повторное агрегирование данных в новые полигоны не требуется, работа может быть закончена на этом этапе.
После создания поверхности интерполяции выполняется агрегирование данных в другой набор полигонов при помощи инструмента Слой площадной интерполяции в полигоны (Areal Interpolation Layer To Polygons). На рисунке ниже иллюстрирован рабочий процесс, в котором на основе данных о степени ожирения школьников города Лос-Анджелес (эти данные распределены по территориям, прикрепленным к отдельным школам) выводятся данные о степени ожирения населения по участкам территориального деления в этом городе.
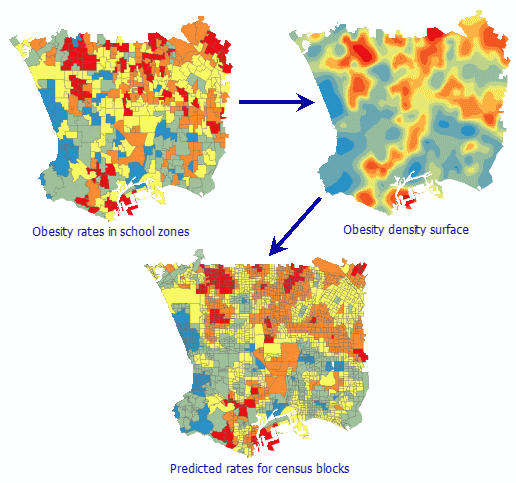
Математическая сторона процессов дезагрегирования и повторного агрегирования рассмотрена в статье, ссылка на которую приведена в конце данного раздела.
Типы данных, которые могут применяться при площадной интерполяции
Площадная интерполяция принимает в качестве входных данных три различных типа наборов полигональных данных. Каждый из этих трех типов может служить основой для построения поверхности интерполяции и поверхности стандартных ошибок, которые затем могут быть агрегированы в целевые полигоны. Интерпретации этой поверхности интерполяции и результатов агрегирования различны для каждого типа данных, как описано ниже.
Усредненные данные (с распределением Гаусса)
Для защиты личной информации или для снижения затрат непрерывные точечные измерения иногда усредняются по определенным территориям, при этом изначальные точечные данные устраняются или держатся в тайне. К примеру, может сообщаться средний уровень загрязнения окружающей среды на определенную территорию, но при этом измерения в отдельных точках держатся в тайне. Без знания о том, где именно происходили измерения степени загрязнения, другие методы на основе кригинга не могут быть использованы.
Для площадной интерполяции непрерывных данных необходимо, чтобы данные имели распределение Гаусса и были усреднены по заданным полигонам. На основе этих полигонов и средних измерений происходит построение поверхности интерполяции (или стандартной ошибки) со значением гауссовой переменной в каждой точке домена данных.
Входные данные
- Исходный набор данных (Source Dataset) – Укажите полигональные объекты.
- Поле значений (Value Field) – Укажите среднее значение для каждого полигона в исходном наборе данных.
При площадной интерполяции гауссовой величины инструмент Слой площадной интерполяции в полигоны (Areal Interpolation Layer To Polygons) вычисляет среднее значение гауссовой переменной (со стандартной ошибкой интерполяции) для целевых полигонов. К примеру, на основе средней температуры во всех областях в данный день может быть вычислена средняя температура в городах этих областей.
Данные в виде отношения (с биномиальным распределением)
Зачастую данные по полигонам получают следующим образом: случайно создается выборка из отдельных элементов генеральной совокупности полигона и подсчитывается количество элементов, имеющих определенную характеристику (такие данные имеют биномиальное распределение). При этом значение имеет процент элементов выборки, имеющих эту характеристику.
Учитывая количество элементов в выборке и количество элементов с определенной характеристикой для каждого полигона, при площадной интерполяции биномиальной величины происходит построение поверхности интерполяции (или поверхности стандартных ошибок) для всех точек домена данных. При этом каждая точка поверхности отражает вероятность того, что элемент выборки, взятый в этом месте, будет иметь данную характеристику.
Допустим, компания выборочно проводит опрос своих клиентов, довольны ли они предоставляемым обслуживанием. В данном случае исследуемой характеристикой является то, что клиент доволен обслуживанием. Точное местоположение всех клиентов в выборке может быть неизвестно; вероятно, компания знает только географический регион (например, код города или области). Площадная интерполяция такой биномиальной величины приведет к построению карты, отражающей места, в которых компания пользуется или не пользуется успехом. Компания затем может провести исследование и выяснить, по какой причине клиенты в определенных регионах более довольны обслуживанием, чем клиенты из других регионов.
Для точной интерполяции выборка должна быть случайной. Каждый элемент генеральной совокупности полигона должен иметь равную вероятность войти в выборку. Если некоторым элементам будет отдаваться предпочтение, полученные значения интерполяции будут иметь систематическую ошибку.
Входные данные
- Исходный набор данных (Source Dataset) – Укажите полигональные объекты.
- Поле значений (Count Field) – Укажите поле, содержащее количество элементов выборки, имеющих определенную характеристику, для каждого полигона.
- Поле выборки (Population Field) – Укажите поле, содержащее общее количество элементов в выборке для каждого полигона.
В случае площадной интерполяции биномиальной величины инструмент Слой площадной интерполяции в полигоны (Areal Interpolation Layer To Polygons) вычисляет процент элементов с определенной характеристикой для каждого указанного полигона. К примеру, если известно число зарегистрированных случаев рака легких для каждого города в области (а вместе с ним и риск заболевания в каждом городе), то можно получить процент населения с раком легких по каждому району в этих городах. Для того чтобы оценить количество случаев рака легких в каждом районе города, нужно умножить полученный процент случаев рака легких на численность населения в данном районе. Таким же образом, умножьте стандартную ошибку на численность населения района, чтобы получить стандартную ошибку оценки количества случаев рака легких в данном районе.
Редкие события (распределение Пуассона с избыточной дисперсией (overdispersed Poisson))
Другой стандартный способ сбора данных по полигонам – подсчет количества происшествий определенного события на заданной территории за указанный период времени. К примеру, экспедиции, наблюдающие за китами, собирают данные, курсируя на судах в заданных областях океана и подсчитывая количество увиденных там китов. В этом случае событием считается увидеть кита. Поскольку количество наблюдаемых китов пропорционально времени наблюдения, необходимо также записывать количество времени, затраченного на подсчет. Каждая такая экспедиция наблюдателей китов будет знать свой полигон (территорию) наблюдения, количество зарегистрированных событий (количество увиденных китов) и время, затраченное на наблюдение.
При площадной интерполяции редких событий будет построена поверхность, отражающая вероятность происхождения какого-либо события в конкретном месте. Чем больше вероятность, тем больше шанс того, что в данном месте будет зарегистрировано это событие. В случае, когда событием является обнаружение физического объекта (такого как кит), поверхность интерполяции может представлять собой карту плотности.
В большинстве реальных случаев, время наблюдения для каждого полигона будет одинаковым. Например, статистика уголовных преступлений обычно имеет форму количества преступлений, произошедших за один год на каждом из полигонов. Поскольку времена наблюдения зачастую равны, если не указано время наблюдения, в алгоритме принимается, что подсчет значений происходил для каждого полигона за одну единицу времени. В случае полного обследования (когда регистрируется каждое произошедшее событие, например, при общей переписи населения) время наблюдения для каждого полигона следует принимать одинаковым.
При наблюдении не обязательно регистрировать каждое событие. Необходимо только, чтобы число событий в единицу времени было пропорционально общей плотности наблюдаемых объектов. На практике это означает, что технология наблюдений должна быть приблизительно одинаковой для каждого полигона. Например, если в одной экспедиции наблюдатель китов более опытен, чем в другой экспедиции, результаты интерполяции будут иметь систематическую ошибку.
Входные данные
- Исходный набор данных (Source Dataset) – Укажите полигональные объекты.
- Поле значений (Count Field) – Укажите поле, содержащее количество событий, зарегистрированных на каждом полигоне.
- Поле времени (Time Field) – Укажите количество времени, затраченное на подсчет событий в каждом полигоне (Необязательный параметр). Если поле оставлено пустым, в алгоритме принимается, что все подсчеты проводились за одну единицу времени.
В случае площадной интерполяции величины с избыточной дисперсией инструмент Слой площадной интерполяции в полигоны (Areal Interpolation Layer To Polygons) вычисляет количество событий в единицу времени для каждого указанного полигона. Например, если наблюдатели китов записывают свое время наблюдения в часах, то вычисленное для нового полигона значение описывает предполагаемое количество китов, которое можно будет наблюдать в этом полигоне за один час. Для данных переписи населения эти значения просто отражают предполагаемую численность населения полигона на момент проведения переписи.
Построение корректной модели
Как и при работе со всеми прочими геостатистическими методами интерполяции, точность результатов площадной интерполяции зависит от точности применяемой модели. По этой причине следует внимательно относиться к построению корректной модели в Мастер операций геостатистики (Geostatistical Wizard).
Поскольку площадная интерполяция в дополнительном модуле ArcGIS Geostatistical Analyst extension реализована на основе метода кригинга, важным этапом построения модели является интерактивная вариография. Зачастую непросто визуально определить качество кривой ковариации, поэтому для каждой эмпирической ковариации (синие перекрестия на рисунке ниже) предоставляются доверительные интервалы (красные вертикальные линии). Если модель ковариации задана верным образом, можно ожидать попадания в доверительные интервалы 90% эмпирических ковариаций. На рисунке ниже 11 из 12 эмпирических ковариаций попадают в пределы доверительных интервалов, а одна точка расположена немного за пределами доверительного интервала. Это указывает на то, что модель хорошо соответствует данным и что полученным результатам можно доверять.
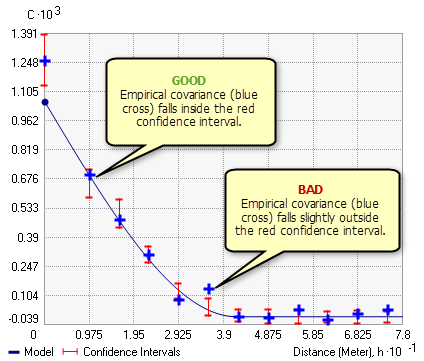
Кривая ковариации по умолчанию во многих случаях плохо соответствует данным. В данном случае необходимо изменить параметры вариографии на втором шаге Мастера операций геостатистики (Geostatistical Wizard) . Построение хорошей кривой ковариации обычно является сложной задачей, для этого необходим навык, вырабатываемый практикой. Тем не менее, существует несколько общих правил построения хорошей модели:
- Уменьшите значение Размер лага (Lag Size) до тех пор, пока эмпирические ковариации не будут полностью положительными.
- Если модель все еще имеет плохое соответствие, попробуйте различные варианты параметра Тип (Type). Модель K-Бесселя (K-Bessel) и Устойчивая (Stable) модель – наиболее функциональны, но также они требуют больше всего времени на обработку.
- Если вам удастся подобрать сочетание параметров Размер лага (Lag Size) и Тип (Type), при котором кривая будет приблизительно соответствовать данным, попробуйте уменьшить значение Шаг решетки (Lattice Spacing). Обратите внимание, что уменьшение шага решетки быстро приводит к возрастанию времени обработки. Параметр шага решетки описан ниже, под заголовком "Новые параметры площадной интерполяции".
Как видно на рисунке ниже, если на втором шаге Мастер операций геостатистики (Geostatistical Wizard) сменить Переменная (Variable) на Вариограмма (Semivariogram), кривая вариограммы для точек (синяя линия на рисунке) может не укладываться в доверительные интервалы. Это не проблема, и критерии для хорошей модели не меняются: если большой процент эмпирических полувариаций попадает в доверительный интервал, то вы можете быть уверены в точности вашей модели.
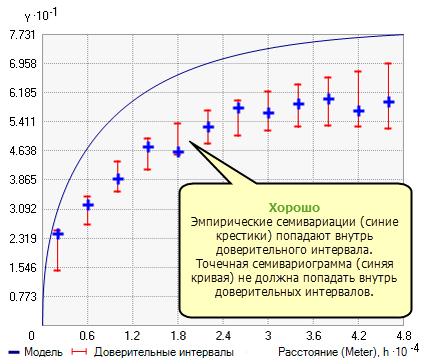
Новые параметры площадной интерполяции
В Мастер операций геостатистики (Geostatistical Wizard) встречаются три параметра, которые не запрашиваются при работе с другими методами кригинга.
- Шаг решетки (Lattice Spacing) – Для оценки точечных ковариаций каждый полигон покрывается сеткой с квадратными ячейками, каждый узел этой сетки принимается за точку. Параметр шага решетки указывает горизонтальное и вертикальное расстояние между точками. Если шаг решетки настолько большой, что в каком-либо полигоне не оказывается точки, точка располагается в центроиде данного полигона. Меньший шаг решетки повысит точность интерполяции, но также это приведет к росту времени обработки. В частности, уменьшение шага решетки вдвое приведет к росту времени обработки в четыре раза.
- Уровень доверительной вероятности (Confidence Level) – Указывает уровень доверительной вероятности для доверительных интервалов кривых вариограммы или ковариации. При корректной модели это значение отражает процент эмпирических ковариаций/вариаций, попадающих в доверительные интервалы. Обратите внимание, что линия точечной вариограммы не обязательно будет попадать в доверительные интервалы. Данный параметр предназначен только для диагностики, его значение не окажет влияния на интерполяцию.
- Параметр избыточной дисперсии (Overdispersion Parameter) – Применяется только для данных типа редких событий (с распределением Пуассона с избыточной дисперсией). В случае с данными, имеющими распределение Пуассона, часто имеет место избыточная дисперсия (overdispersion) – в этом случае изменчивость модели больше ожидаемой. Параметр избыточной дисперсии помогает исправить такое положение вещей. Этот параметр равен обратному параметру дисперсии в случае негативного биномиального распределения.
Все прочие параметры имеют то же значение, что и в других методах на основе кригинга.
Ограничения
Как и все методы кригинга, площадная интерполяция имеет несколько ограничений, которые предотвращают построение корректной модели данных.
Нестационарность
Одно из самых жестких приближений модели кригинга – предположение о стационарности данных. Стационарность предполагает, что статистические отношения между значениями данных в двух любых полигонах зависят только от расстояния между этими полигонами. К примеру, население страны сосредоточено в городах, тогда как на территории между городами живет мало людей. Для площадной интерполяции это является проблемой, поскольку, при условии стационарности, плотность населения должна изменяться на местности равномерно – не должно быть крайне высокой плотности населения рядом с областями крайне низких плотностей. Для подобных нестационарных данных подбор корректной модели площадной интерполяции представляет собой очень сложную, а временами и вовсе непосильную задачу.
Полигоны с большой разницей в размерах
Если некоторые полигоны имеют очень малую площадь по сравнению с большими полигонами, есть вероятность того, что алгоритм не сможет различить меньшие полигоны и будет считать их совпадающими. Это происходит оттого, что параметр шага решетки приводит к дискретизации полигонов, таким образом, одна точка решетки может представлять несколько полигонов. Это приведет к ошибке, поскольку площадная интерполяция не поддерживает совпадающие полигоны. Для решения этой проблемы воспользуйтесь такими действиями:
- Используйте инструменты Найти идентичные (Find Identical) и Удалить идентичные (Delete Identical) для поиска и удаления совпадающих полигонов. Если совпадающих полигонов не найдено или если их удаление не решает проблемы, переходите к следующему этапу.
- Вручную уменьшите шаг решетки, пока алгоритм не сможет различать все полигоны. Однако уменьшение шага решетки приведет к резкому росту времени вычислений. Если окажется, что необходимый шаг решетки требует слишком большого времени обработки, переходите к следующему этапу.
- Уберите из выборки самые меньшие полигоны в классе пространственных объектов, чтобы они не применялись при расчетах.
Литература
- Krivoruchko, K., A. Gribov, E. Krause (2011). "Multivariate Areal Interpolation for Continuous and Count Data," ("Многомерная площадная интерполяции для непрерывных и дискретных данных,") Procedia Environmental Sciences, Volume 3 (Том 3): 14–19.