Доступно с лицензией Spatial Analyst.
Логика неразличимости может использоваться как метод анализа наложения для решения традиционных приложений анализа наложения, например, выборка территории и модели пригодности.
Основная предпосылка логики неразличимости в том, что есть неточности в атрибуте и в геометрии пространственных данных. Логика неразличимости обеспечивает методы для решения двух типов неточности, но логика неразличимости, т.к. она относится к анализу наложения, фокусируется на неточности в атрибутивных данных. Две основные области, где в атрибутивных данных возникают неточности, возникают в определении классов и в измерении явления. Оба эти источника неточностей, особенно в определении классов, может привести к неточности в присвоении ячеек конкретным классам.
Определение классов в классификации и неточность в присвоении явлений на классам могут повлиять на принятие решений. Инструменты Нечеткое наложение (Fuzzy Overlay) помогают принимать решения с учетом этих неточностей. Логика неразличимости сосредоточена на моделировании неточностей класса границ.
Инструменты Взвешенное наложение (Weighted Overlay) и Взвешенная сумма (Weighted Sum) основаны на четких наборах, где каждая ячейка либо находится в классе, либо нет. При логике неразличимости специально рассматриваются ситуации, когда границы между классами не ясны. В отличие от четких наборов, для логики неразличимости не важно положение внутри или вне класса. Она определяет, насколько вероятно, что это явление является членом набора (или класса). Логика неразличимости основана на теории множеств, поэтому необходимо определить возможности, а не вероятности.
Например, в модели пригодности жилья, если уклон является одним из входных критериев, каждое значение уклона будет трансформировано или присвоено значение от 0 до 1 на возможности того, что значения уклона будут членом набора пригодности для построения (или класса) – будут подходящими. Значение 1 указывает на не полную уверенность того, что значение находится в наборе, а 0 указывает с полной уверенностью, что оно не находится в наборе. Все другие значения – некоторого уровня возможности, и чем выше значение, тем больше вероятность принадлежности. Процесс трансформации исходных входных значений в масштаб 0 к 1 возможности принадлежности называется процессом подготовки задачи для решения методами логики неразличимости. Каждый критерий для модели, например, экспозиция, расстояние до дорог и тип землепользования будут обработаны методами логики неразличимости. Инструмент Нечеткое множество (Fuzzy Membership) используется для трансформации данных в масштаб возможности 0 к 1.
Чтобы определить местоположения, которые лучше всего отвечают всем критериям – т.е. имеют высокую вероятность принадлежности во всех наборах – используется инструмент Наложение неразличимости (Fuzzy Overlay). При комбинировании нескольких критериев, инструмент Наложение неразличимости (Fuzzy Overlay) рассматривает вероятность ячейки быть членом каждого набора, определенного несколькими критериями. Например, какова вероятность того, что определенное местоположение принадлежит благоприятной пригодности для уклона, экспозиции и расстояния до дорог?
Таким образом, два основных шага в анализе логики неразличимости – это подготовка задач для решения методами логики неразличимости или процесс нечеткого множества и анализ наложения неразличимости. Эти два шага коррелируют с шагами переклассифицировать/трансформировать и добавить/комбинировать, соответственно, в общем процессе наложения.
Принадлежит ли что-либо классу или нет, часто не ясно, но субъективно. На человеческом языке, определяется количество этих неточностей через модификаторы, такие как очень, немного, и умеренно. Логика неразличимости выполняет анализ наложения более сходно с естественным человеческим мышлением. Вещи не четкие, границы могут быть неразличимыми. Логика неразличимости не является анализом неопределенности в данных, но вместо этого исследует неточность в классе границ.
В следующих разделах будут обсуждаться вопросы классификации данных, нечеткие множества и выполнение нечеткого наложения. Также ниже обсуждается сравнение логики неразличимости в методах анализа двоичного и взвешенного наложения и то, как логика неразличимости интегрируется в общий процесс наложения.
Классификация данных и логика неразличимости
Для описания явлений и расположения их по порядку вы, как правило, определяете их в классы. Категория землепользования, тип почвы, взвешивание пригодности, класс дорог и типа растительности – это примеры классов. В нечетких наборах, принадлежность – двоичная, и явление либо находится в классе, либо нет. Границы класса – четкие. Но из-за неточности мысли, двусмысленных правил категоризации, неопределенности и двойственности, границы между классами не всегда ясные.
Например, если изучаемым явлением является отношение различного роста людей в группе, вы можете начать путем кластеризации разных людей на классы, исходя из их роста. Вы можете начать с трех классов – короткого, среднего и высокого. Вам нужно установить границы для классов. Например, рост невысокого человека может быть 5 футов (1,524 метра) или ниже, высокого человека – 6 футов (1,8288 метра) и выше, и человека среднего роста – от 5 до 6 футов (от 1,6764 до 1,8288 метра). Если рост человека – 6 футов (1,8288 метров), они будут помещены в класс высоких. Если рост человека – 5' 11" (1,8034 метра), они будут классифицированы как средние. С разницей только в 1 дюйм ( 0,0254 метра) между ростом двух людей, они помещаются в разные классы. Это отношение различия может быть изображено, если рост члена другой группы – 5' 1" (1,5494 метра), а второго – 6' 6" (1,9812 метра). Из-за грубости классификации, полные отношения между ростом не могут быть охвачены.
Чтобы более правильно изобразить отношения роста между разными людьми, может быть добавлено больше классов. Например, можно добавить еще два класса – низкий рост – 4' 10" (1,4732 метра) или меньше, средний рост – от 4' 10" (1,4732 метра) до 5' 4" (1,6256 метра), средняя высота будет от 5' 4" (1,6256 метра) до 5' 10" (1,778 метра), средний рост будет от 5' 10" (1,778 метра) до 6' 4" (1,9304 метра), и рост будет больше 6' 4" (1,9304 метра). С этим уточнением в классах, отношение между высотой людей может быть более точно охвачено.
Для дальнейшего уточнения можно добавить еще больше классов. Независимо от того, сколько классов добавляется, все равно есть генерализация отношения высоты между людьми. Есть некоторые явления, которые не могут быть классифицированы в строго определенные классы. Иногда трудно группировать явления реального мира на отдельные классы.
Как видно, определение границ класса может быть субъективным и может изменяться с определением явления. В определенных классах высот выше, предполагается, люди взрослые, скорее всего, и мужчины и женщины. Определения классов возможно придется изменить, если группа полностью состоит из женщин. Границы класса возможно придется изменить еще больше, если группа состоит из детей или включает их.
Определение классов и характеристики явления диктует, как представлять моделируемое явление. Погрешность измерения еще более усугубляет проблему классификации. Если процедура измерения роста людей имеют точность плюс-минус 1 дюйм (0,0254 метра), то погрешность может изменить класс, к которому явление присваивается.
Логика неразличимости моделирует эту неопределенность в процессе классификации. В логике неразличимости классы определены как наборы. Существует понимание того, каково идеальное значение для принадлежности в наборе, например, идеальное значение уклона в модели пригодности жилья. По мере удаления значений от идеала, уровень четкости уменьшается до определенной точки, где ясно, что значение не является членом набора (например, это определенно слишком крутой уклон, чтобы строить на нем).
Например, в приложении высоты выше, если вы останетесь с тремя классами высоты – коротким, средним и высоким – три класса в логике неразличимости могут перекрываться.
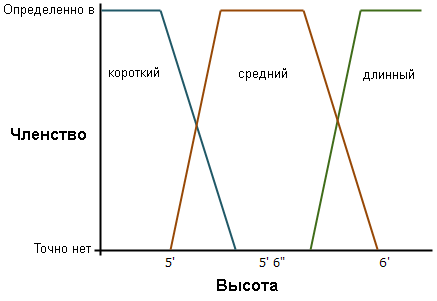
На рисунке выше полная принадлежность каждому классу:
- Короткий: < 5 футов (1,524 метра)
- от 5' 3 1/2" (1,6129 метра) до 5' 8 1/2" (1,7399 метра)
- Высокий: > 6 (1,8288 метра)
Для набора (или класса) низких, человек 5 футов (1,524 метра) или меньше, безусловно, находится в пределах небольшого набора и присваивается 1. Любая высота больше 5 футов (1,524 метра) и меньше 5' 3 1/2" (1,6129 метра) расположена между наборами (или классами) низких и средних. Для высот от 5 футов (1,524 метра) до 5' 1 3/4» (1,6193 метра), высоты скорее всего будут в наборе низких. Высоты большие 5' 1 3/4» (1,6193 метра) и меньшие или равны 5' 3 1/2» (1,6129 метра), возможно, в наборе низких, но имеют большую возможность быть частью набора средних.
Процесс подготовки задачи для решения методами нечеткой логики осуществляется обычно через заданные функции с использованием инструмента Нечеткое множество (Fuzzy Membership).
Нечеткое множество
Процесс подготовки задачи для решения методами логики неразличимости характеризует неточность классов для явлений, которые не имеют четких границ.
Подготовка задачи для решения методами логики неразличимости конвертирует исходные значения явления для возможности того, что они принадлежат к определенному набору. Определенный набор может состоять из пригодных или на благоприятном расстоянии или имеющих возможность нахождения указанного минерала. Исходные значения явления переклассифицируются на этом континууме принадлежности через предопределенные функции принадлежности неразличимости или с помощью других методов классификации.
В процессе подготовки задачи для решения методами логики неразличимости, дается идеальное определение для принадлежности набору. Каждому значению этого явления, более центральному к центру определения набора, будет присвоено 1. Тем значениям, которые, безусловно, не являются частью набора, присваивается 0. Те значения, которые находятся между двумя крайними значениями, попадают в переходную зону набора, границу. Т.к. значения отдаляются от идеала или центра набора, они присваиваются уменьшающемуся значению в непрерывном масштабе 1 к 0. Т.к. присвоенное значение уменьшается, то исходное значение явления имеет меньше возможности быть членом этого набора.
Значение подготовки задачи для решения методами логики неразличимости, равное 0,5, – это точка кроссовера. Нечеткое значение больше 0,5 подразумевает, что значение исходного явления может быть членом набора. Когда значение подготовки задачи для решения методами логики неразличимости опускается ниже 0,5, меньше вероятности, что значение исходного явления является членом набора; значения могут не быть частью набора.
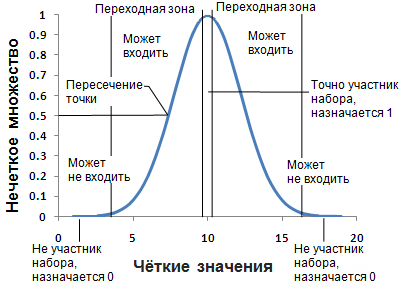
Ширина переходной зоны зависит от моделируемого явления, что известно о явлении, определения набора и точности измерения. Изменяя параметры функции подготовки задач, можно определить характеристики переходной зоны. На рисунке ниже функция Нечеткое Гауссово (Fuzzy Gaussian) показана тремя разными кривыми, полученными из изменения параметров функции.
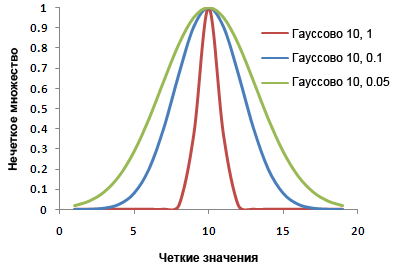
Параметры служат модификаторами для определения набора. Модификаторы характеризуют возможное наложение или среднюю группу между наборами.
Процесс переклассификации для каждого критерия происходит в анализе наложения.
Алгоритмы нечеткого наложения
Чтобы проанализировать отношения и взаимодействия между всеми наборами для нескольких критериев модели наложения, используются методы нечеткого наложения. Т.к. процесс переклассификации основан на степени принадлежности набору, то методы наложения описывают взаимодействия неточности в принадлежности наборов. Методы наложения неразличимости основаны на теории множеств. Теория множеств – это математическая дисциплина, определяющая количество отношения принадлежности явление конкретным наборам. В нечетком наложении, в целом, набор соответствует классу.
Доступные методы наложения нечеткого наложения : нечеткий И (fuzzy And), нечеткий ИЛИ (fuzzy Or), нечеткое произведение (fuzzy Product), нечеткая сумма (fuzzy Sum) и нечеткая Гамма (fuzzy Gamma). Каждый из этих методов описывает отношение принадлежности ячейки входным наборам. Например, тип наложения нечеткий И (fuzzy And) создает выходной растр, где каждому значению ячейки дается минимальное присвоенное нечеткое значение для каждого из наборов, к которому принадлежит ячейка. Если анализ наложения – это модель пригодности жилья и каждый из нескольких критериев был fuzzified относительно ее принадлежности к подходящим наборам, нечеткий И определяет низкую возможность ячейки принадлежать к одному из подходящих наборов в нескольких критериях.
Нечеткий ИЛИ выдает максимальное значение пересечения наборов. Т.е. в модели пригодности жилья высокая потенциальная принадлежность (большое значение пригодности) для каждой ячейки оценивается по нескольким критериям.
Бинарное, взвешенное наложение и наложение логики неразличимости
Во многих описаниях логики неразличимости для анализа наложения, она сравнивается с анализом бинарного наложения. В анализе бинарного наложения для каждого критерия, каждая ячейка оценивается по тому, находится ли она в заданном классе или нет. Как было указано выше, во многих случаях может быть трудно определить четкие границы класса и окончательно присвоить ячейки конкретным классам. В бинарном анализе, в случае модели пригодности жилья, каждая ячейка присваивается как пригодная (1) или нет (0) для каждого критерия. В процессе наложения, ячейки, которым присваивается 1 для всех входных критериев, считаются потенциально подходящими ячейками.
Ограничения подхода анализа бинарного наложения:
- Если ячейка соответствует не всем критериям, не определено второй лучшей опции.
- Нет относительного взвешивания ячеек, которые отвечают критерию.
- Обсуждаемые выше проблемы по вопросу процесса классификации.
Анализ Взвешенное наложение пытается разрешить эти ограничения. Вместо классификации каждой ячейки в бинарном масштабе 1 или 0, Взвешенное наложение (Weighted Overlay) присваивает значение каждой ячейки на определенном непрерывном масштабе, например 1 к 10, где 10 – наиболее предпочтительное относительно критерия. Непрерывный масштаб предоставляет больше градаций классов, что дает больше уточнения представления явления. Для каждого критерия, каждой ячейки присваивается масштабу 1 к 10. Все переклассифицированные критерии затем объединяются. Ячейки с наибольшими суммированными значениями наиболее предпочтительны относительно входного критерия. Чем более благоприятный критерий каждых из входных данных, тем лучше.
Нечеткое наложение и взвешенное наложение более схожи друг с другом, чем с бинарным наложением, однако они строятся по-разному. Нечеткое наложение основано на теории множеств, в то время как взвешенное наложение – на линейных комбинациях. Оба метода трансформируют исходные значения. Для нечеткого наложения трансформация определяет возможность принадлежности к наборам, в то время как взвешенное наложение происходит на относительном масштабе предпочтений. Т.к. эти два метода уникальны, то инструменты для выполнения анализа между несколькими критериями не являются взаимозаменяемыми.
Логика неразличимости и общий процесс анализа наложения
Анализ наложения логики неразличимости следует общим шагам анализа наложения, но с большим упором на определенные шаги, с меньшим – на другие, и разным смыслом значений присвоенных чисел, относительно других подходов анализа наложения.
Общие шаги анализа наложения:
- Определите проблему.
- Разбейте проблему на подмодели.
- Определите значащие слои.
- Переклассифицируйте или трансформируйте данные в слое.
- Взвесьте входные слои.
- Добавьте или комбинируйте слои.
- Проанализируйте.
Как в случае со всеми анализами наложения, шаги 1 – 3 сходны для анализа нечеткой логики. Т.к. логика неразличимости основана на наборах, то смысл переклассифицированных значений (шаг 4) и методы анализа, которые могут использоваться для комбинирования нескольких критериев (шаг 6), делают нечеткую логику уникальной относительно других подходов анализа наложения.
В следующих разделах обсуждаются отличия логики неразличимости в шагах 4 – 7.
Переклассифицируйте или трансформируйте данные в слое
Входные данные переклассифицируются или трансформируются в масштабе 0 к 1, определяя возможность принадлежать заданному набору. Этот процесс переклассификации или подготовки задачи для решения методами логики неразличимости осуществляется в рамках инструмента Принадлежность неразличимости (Fuzzy Membership). Ряд функций принадлежности был разработан для помощи в этом процессе трансформации. Доступные функции: fuzzy Gaussian, fuzzy Large, fuzzy Linear, fuzzy MSLarge, fuzzy MSSmall, fuzzy Near и fuzzy Small. Каждая функция принадлежности трансформирует данные определенным способом для захвата взаимодействия явления.
Взвесьте входные слои
Т.к. логика неразличимости основана на теории множеств и вы определяете, принадлежит ли конкретное местоположение одному или нескольким наборам, взвешивание не имеет смысла. Увеличение веса одного фактора над другим не может увеличить возможность принадлежать одному набору или комбинации нескольких наборов. Ячейка либо является членом набора, либо нет (наряду с другими промежуточными степенями). При нечетком наложении взвешивание критериев не применяется.
Добавьте или комбинируйте слои
В шаге Добавить или комбинировать, логика неразличимости исследует взаимодействие возможности явления принадлежать к нескольким наборам, в отличие от взвешенного наложения и взвешенной суммы, которые основаны на идее, что чем более благоприятными являются элементы, тем лучше результат.
Для взвешенного наложения существуют определенные методы исследования этого относительного отношения и для определения количества взаимодействия. Подходы комбинации: нечеткий И (fuzzy And), нечеткий ИЛИ (fuzzy Or), нечеткое произведение (fuzzy Product), нечеткая сумма (fuzzy Sum) и нечеткая Гамма (fuzzy Gamma). Каждый из этих наборов основан на теории множеств и специфичен для анализа взвешенного наложения.
Анализ
Как и в случае с любым анализом наложения, вам решать – нужно ли анализировать и интерпретировать результаты. Но из-за различных смыслов переклассифицированных значений и методов наложения, лежащих в основе каждого подхода наложения, различные механизмы, возможно, должны быть использованы для оценки достоверности полученных результатов.