Доступно с лицензией Geostatistical Analyst.
Моделирование вариограммы/ковариации – это ключевой шаг между пространственным описанием и пространственной интерполяцией. Основное применение геостатистики – прогноз значений данных в неопорных местоположениях.
Эмпирическая вариограмма м ковариация предоставляют информацию о пространственной автокорреляции наборов данных. Однако они не предоставляют информацию для всех возможных направлений и расстояний. По этой причине и для того, чтобы убедиться, что проинтерполированные значения кригинга имеют положительные дисперсии кригинга, нужно подобрать модель (т. е. непрерывную функцию или кривую) к эмпирической вариограмме/ковариации.
Более подробно о связи между вариограммами и ковариацией
Различные виды значений эмпирической вариограммы/ковариации
Мастер операций геостатистики предоставляет три вида значений эмпирической вариограммы/ковариации. Для помощи при подборе модели к данным можно использовать один, два или все три вида. Вид по умолчанию отображает объединенные в бины и усредненные значения эмпирической вариограммы/ковариации.
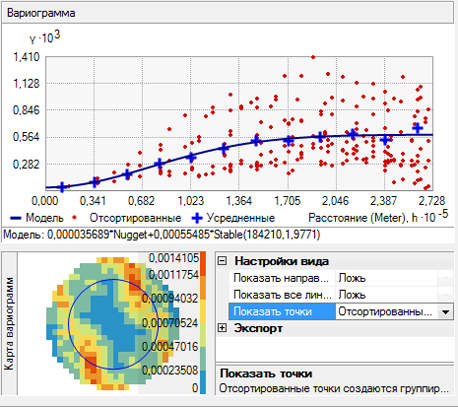
Объединенные в бины значения отображены красными точками и получены с помощью группировки (биннинга) точек эмпирической вариограммы/ковариации с использованием квадратных ячеек со стороной равной размеру одного лага. Средние значения отображены синими перекрестьями и получены с помощью биннинга точек эмпирической вариограммы/ковариации, попадающих в угловые сектора. Объединенные в бины точки показывают локальную вариацию значений вариограммы/ковариации, а средние значения – сглаженную дисперсию значений вариограммы/ковариации. В большинстве случаев модель проще подобрать к усредненным значениям, так как они предлагают более упорядоченный вид пространственной автокорреляции данных и отображают более сглаженные изменения значений вариограммы, чем объединенные в бины точки.
Элемент управления Показывать точки (Show points) можно установить в значение Объединенные в бины и усредненные (Binned and Averaged) (как показано на рисунке ниже), Объединенные в бины (Binned) или Усредненные (Averaged) (как показано на рисунке ниже).
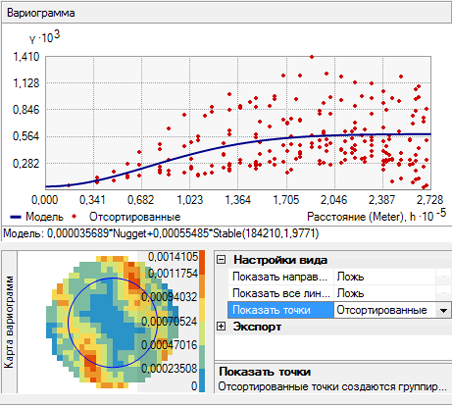
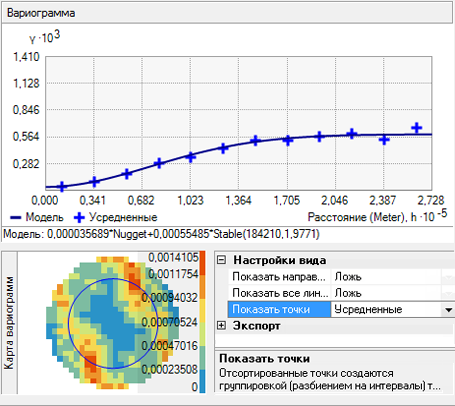
Дополнительно с помощью опции Показать все линии к изображению могут быть добавлены зеленые линии. Линии – это локальные полиномы, подобранные к объединенным в бины эмпирической вариограммы/ковариации. Если опция Показать направление поиска имеет значение Истина, отображается только локальный полином, подобранный к поверхности эмпирической вариограммы/ковариации перпендикулярно центральной оси инструмента Показать направление поиска, как показано на следующем рисунке:
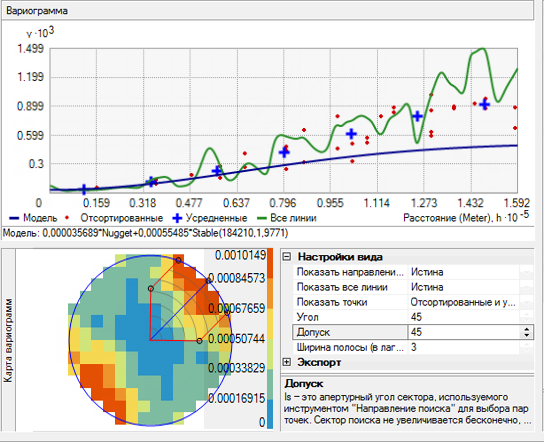
Модель вариограммы/ковариации, подобранная к эмпирическим данным, должна:
- Проходить через центр облака объединенных в бины значений (красные точки);
- Проходить как можно ближе к средним значениям (синие перекрестья);
- Проходить как можно ближе к середине локальных полиномов (зеленым линиям).
Имейте в виду, что ваши знания этого явления могут диктовать форму модели, а также ее самородок, диапазон, частичный порог и значения анизотропии, даже если модель не слишком хорошо соответствует эмпирическим данным (помните, что эмпирические данные – просто образец реального явления, которое вы хотите моделировать, и не могут полностью представлять все его пространственные и статистические аспекты).
Различные типы моделей вариограммы/ковариации
В Geostatistical Analyst предусмотрены следующие функции вариограммы/ковариации для моделирования эмпирической вариограммы:
- Круговая
- Сферическая
- Тетрасферическая
- Пентасферическая
- Экспоненциальная
- Гауссова
- Рациональная квадратическая
- Эффекта дыры
- K-Бесселя
- J-Бесселя
- Устойчивая
Выбранная модель влияет на интерполяцию неизвестных значений, особенно если форма кривой вблизи исходных данных значительно отличается. Чем круче кривая вблизи исходных данных, тем больше влияния на интерполяцию будет иметь ближайшая окрестность.
В результате выходная поверхность будет менее сглаженной. Каждая модель разработана для более точного соответствия разных типов явления.
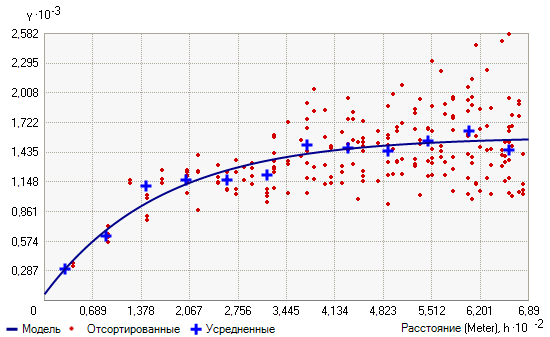
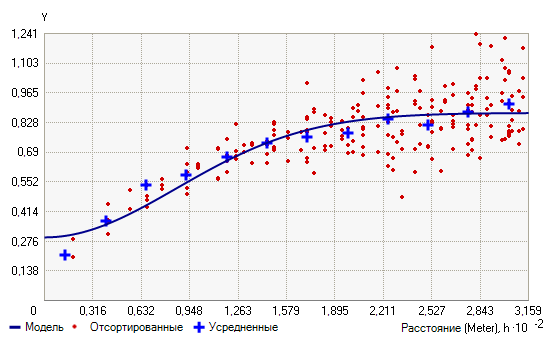
На диаграммах ниже показаны две основные модели и в чем заключается функциональное отличие одной модели от другой. На первом рисунке показана экспоненциальная вариограмма, а на другом – вариограмма по гауссовому (нормальному) распределению: