Доступно с лицензией Geostatistical Analyst.
Прежде чем создавать окончательную поверхность, необходимо понять, насколько точно модель позволяет интерполировать значения в неизвестных точках. Перекрестная и обычная проверки помогают принять обоснованное решение относительно выбора модели, которая обеспечит лучшую интерполяцию. Вычисление статистики служит инструментом диагностики, который показывает, приемлемы ли модель и/или значения связанных с ней параметров.
Перекрестная и обычная проверки основаны на следующем принципе: удаление одного или нескольких местоположений данных и интерполяция связанных с ними значений с использованием данных в оставшихся местоположениях. Таким образом, можно сравнить интепролируемое значение с наблюдаемым и получить полезную информацию о качестве модели кригинга (например, о параметрах вариограммы и окрестности поиска).
Перекрестная проверка
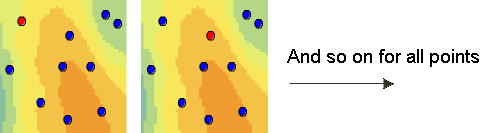
Перекрестная проверка использует все данные для оценки моделей тренда и автокорреляции. В ходе этой проверки по очереди удаляются все местоположения данных и интерполируется связанное значение. Например, на приведенной ниже схеме показаны 10 точек данных. Перекрестная проверка пропускает точку (красную точку) и рассчитывает значение в этом местоположении, используя 9 остальных точек (синие точки). Затем выполняется сравнение интерполируемого и фактического значений в месте пропущенной точки. Эта процедура повторяется для второй точки и т. д. Перекрестная проверка сравнивает измеренные и интерполируемые значения для всех точек. В некотором смысле перекрестная проверка немного «обманывает», используя все данные для оценки моделей тренда и автокорреляции. По завершении перекрестной проверки некоторые местоположения данных, если они содержат существенные ошибки, могут быть исключены как аномальные, что потребует исправления моделей тренда и автокорреляции.
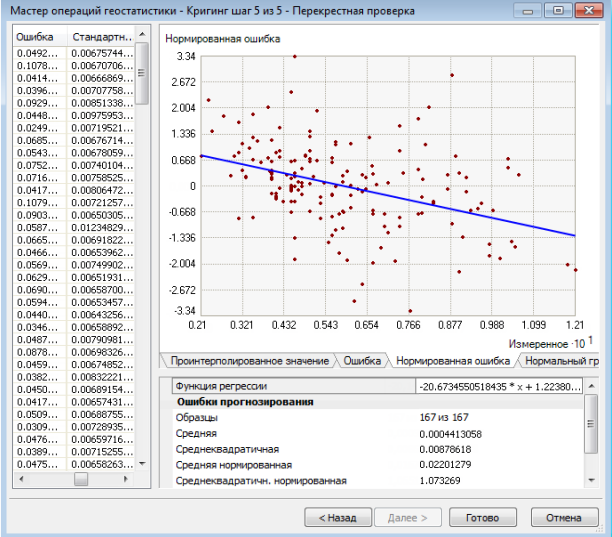
Перекрестная проверка выполняется автоматически, и ее результаты отображаются в последнем шаге Мастера геостатистики. Перекрестную проверку можно также выполнить вручную с помощью инструмента геообработки Перекрестная проверка.
Проверка
Проверка сначала удаляет часть данных (назовем ее тестовым набором данных). Затем на основе оставшихся данных (учебного набора данных) разрабатываются модели тренда и автокорреляции, которые будут использоваться для интерполяции. В Geostatistical Analyst для создания тестового и учебного наборов данных применяется инструмент Поднабор объектов. В остальном типы графиков и сводной статистики, которые используются для сравнения интерполируемых и истинных значений, одинаковы для обычной и перекрестной проверок. Обычная проверка создает модель только для поднабора данных, поэтому она не позволяет проверить напрямую окончательную модель, которая должна включать все доступные данные. Обычная проверка позволяет удостоверить правильность протокола решений, например, касающихся выбора модели вариограммы, размера лага и окрестности поиска. Если протокол решений работает для проверки, то это гарантирует, что он также будет работать для всего набора данных.
Проверку модели можно выполнить с помощью инструмента геообработки Слой GA в точки. Более подробно о проверке модели см. в разделе Использование проверки для оценки моделей.
Графики
Geostatistical Analyst предусматривает несколько диаграмм и сводок по сравнению измеренных значений с прогнозируемыми на последней странице Мастера геостатистики. Ниже приведена диаграмма рассеивания интерполируемых значений относительно истинных. Можно было бы ожидать, что точки должны рассеиваться относительно линии 1:1 (серая линия на приведенном ниже графике). Однако уклон обычно меньше 1. Это особенность кригинга, который обычно при интерполяции занижает большие значения и завышает малые, как показано на следующем рисунке:
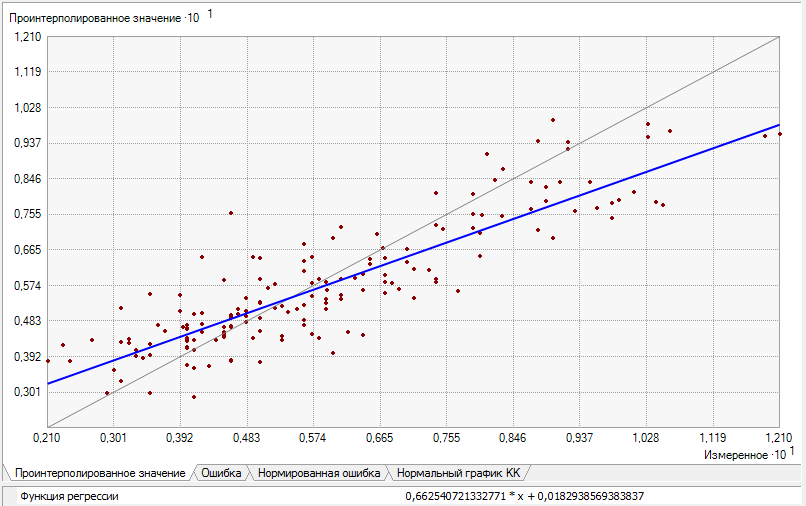
Подобранная линия, проходящая через область рассеивания точек, показана синим цветом, а уравнение приведено сразу под графиком. График ошибок аналогичен графику интерполяции, только измеренные значения вычитаются из прогнозируемых значений. Для графика нормированных ошибок разность измеренных и прогнозируемых значений делится на оценку стандартных ошибок кригинга. Все эти три графика показывают точность интерполяции кригинга. Если все данные были независимыми (нет автокорреляции), все интерполированные значения будут одинаковыми (каждое из них должно быть средним от измеренных данных), и потому синяя линяя будет горизонтальной. При наличии автокорреляции и хорошей модели кригинга синяя линия будет приближаться к серой линии 1:1. Уравнение локальной регрессии под каждой из этих трёх диаграмм рассчитывается с помощью уравнения устойчивой регрессии. Этот процесс сначала размещает линию стандартной линейной регрессии на диаграмму рассеивания. Далее удаляются все точки, которые больше чем на два стандартных отклонения выше или ниже линии регрессии, и затем подсчитывается новое уравнение регрессии. Этот процесс гарантирует, что несколько выбросов не повлияют на целое уравнение регрессии.
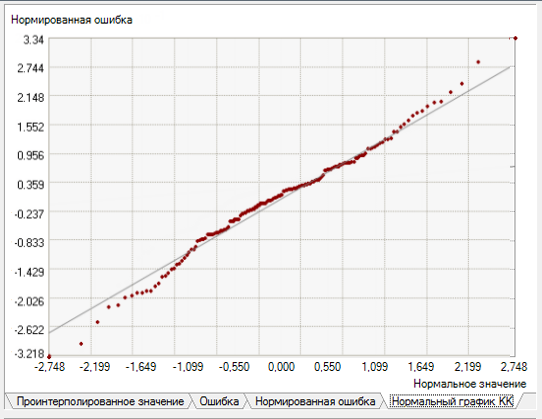
Нормальный график КК показывает квантили разности между интерполируемыми и измеренными значениями, а также соответствующие квантили из стандартного нормального распределения. Если отклонения интерполируемых значений от истинных значений распределены по нормальному закону, точки должны располагаться примерно вдоль серой линии. Если ошибки распределены по нормальному закону, то можно уверенно использовать методы, основанные на этом законе (например, карты квантилей в простом кригинге).
Статистика ошибок интерполяции
Наконец, ниже приведены некоторые сводные статистические данные по ошибкам интерполяции кригинга. Используйте эти данные для диагностики. Этот диагностический расчет можно выполнить с помощью инструмента Перекрестная проверка или Мастера геостатистики.
- Желательно, чтобы интерполированные значения были несмещенными (центрированными относительно истинных значений). Если ошибки интерполяции несмещенные, то средняя ошибка интерполяции стремится к нулю. Однако это значение зависит от шкалы данных; для нормирования значений вычисляются нормированные ошибки кригинга, которые определяются как частное от деления ошибок интерполяции на стандартные ошибки интерполяции. Среднее этих ошибок также стремится к нулю.
- Желательно получить приемлемую оценку неопределенности, стандартные ошибки интерполяции. Каждый из методов кригинга дает оценку стандартных ошибок интерполяции. В дополнение к интерполяции, выполняется оценка отклонений интерполируемых значений от истинных (изменчивость). Важно получить правильную изменчивость. Например, в случае ординарного, простого, универсального и эмпирического байесова кригинга (предполагающего, что данные распределены по нормальному закону) карты квантилей и вероятности зависят от стандартных ошибок кригинга столь же существенно, как от самих интерполированных значений. Если средние стандартные ошибки близки к среднеквадратическим ошибкам интерполяции, оценка изменчивости интерполяции выполнена правильно. Если средние стандартные ошибки больше, чем среднеквадратические ошибки интерполяции, оценка изменчивости интерполяции выполнена с переоценкой. Если средние стандартные ошибки меньше, чем среднеквадратические ошибки интерполяции, оценка изменчивости интерполяции выполнена с недооценкой. Другой способ определить этот параметр – разделить каждую ошибку интерполяции на соответствующую оценку стандартной ошибки интерполяции. В среднем они должны быть равны друг другу, так что среднеквадратические ошибки интерполяции стремятся к 1, если стандартные ошибки интерполяции рассчитаны правильно. Если среднеквадратические нормированные ошибки интерполяции больше 1, оценка изменчивости интерполируемых значений занижена; если среднеквадратические нормированные ошибки интерполяции меньше 1, оценка изменчивости интерполируемых значений завышена.