Как работает инструмент Фильтрация в водоносном горизонте

Доступно с лицензией Spatial Analyst.

Перемещение растворов в пористой среде включает два основных механизма: адвекцию и гидродинамическую дисперсию. Адвекция описывает пассивное перемещение растворенного вещества с транспортирующей жидкостью. Дисперсия – это процесс перемешивания растворенного вещества с жидкостью при дифференциальном движении жидкостей через поровое пространство. Инструмент Фильтрация в водоносном горизонте предполагает, что водоносный горизонт является вертикально перемешанным, то есть концентрация вещества по всей вертикальной толще одинакова. Это позволяет применять математическую модель в двух измерениях, что и требуется растровой моделью данных.

Двухмерная дисперсия

Двухмерная дисперсия в пористой среде может быть описана уравнением адвекции-дисперсии (Bear, 1979; Freeze and Cherry, 1979; и Marsily, 1986), сформулированного в терминах продольного (в направлении потока) и поперечного (перпендикулярно направлению потока) направлений X_L и X_T соответственно, как показано ниже.

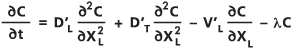
• , где:

  C : Концентрация раствора как функция двух пространственных измерений и времени t.

  ∂C/∂t : Представляет производную по времени.

  D'_L : Коэффициенты эффективной (замедленной) дисперсии в продольном направлении.

  D'_T : Коэффициенты эффективной (замедленной) дисперсии в поперечном направлении.

  λ : Коэффициент распада принимается постоянным для экспоненциального распада первого порядка.

Коэффициенты дисперсии

Коэффициент дисперсии – это мера области простирания растворенного вещества в заданном направлении:

D'_i = D_i/R

• , где:

  R : Фактор замедления.

  i : Направление (поперечное и продольное).

Коэффициент дисперсии характеризует поведение растворенного вещества в конкретной среде.

Отношение между коэффициентом дисперсности и дисперсии

Дисперсности α_L (продольная дисперсность) и α_T(полученная по доле дисперсности) связаны с коэффициентами дисперсности следующим образом:

D'_L = α_L V' и

D'_T = α_T V'

• , где:

  V' : Средняя замедленная скорость фильтрации.

  X_L : Смещение в продольном направлении, параллельном направлению потока в центре масс.

  X_T : Смещение в поперечном направлении, перпендикулярном направлению потока в центре масс.

  V'_L : Замедленная скорость растворенного вещества в продольном направлении.

В потоке грунтовых вод:

V = q / n

• , где:

  q : Сток по Дарси (расход через единичное поперечное сечение).

  n : Эффективная пористость геологической формации.

V' = V / R

Обратитесь к разделу, посвященному инструменту Скорость по Дарси за более подробным обсуждением скоростей транспортировки жидкости в грунтовых водах.

Гауссова дисперсия

Приближенное решение этого уравнения, используемое инструментом Фильтрация в водоносном горизонте, основывается на допущении, что Гауссова дисперсия от мгновенного точечного источника в двухмерной области при начальной концентрации раствора, равной нулю, (например, для чистого, вертикально перемешанного водоносного пласта), вычисляется по следующему уравнению:

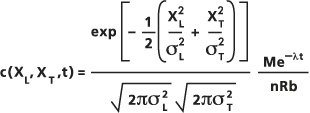
• , где:

  M : Масса растворенного вещества, выпущенного мгновенно в каком-либо источнике, в единицах массы.

  n : Пористость водоносного пласта.

  R : Фактор замедления.

  b : Толщина водоносного пласта в единицах длины.

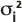  : дисперсия Гауссова распределения в продольном и поперечном направлениях, определяемая как функция продольной дисперсности и доли дисперсности, задаваемой пользователем, и длины пути перемещения центра масс растворенного вещества, получаемого из файла трека.

Общая эллиптическая форма функции двумерного Гауссова распределения проиллюстрирована на рисунке, приведенном внизу:

Форма бивариантного Гауссова распределения

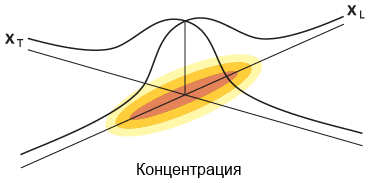
Существует несколько значительных ограничений и допущений, реализованных в решении для инструмента Фильтрация в водоносном горизонте. Эллипс дисперсии центрирован на центре масс растворенного вещества, который, как предполагается, движется вдоль траектории движения потока, охарактеризованной во входном файле трека. Ориентация эллипса также фиксируется на траектории движения потока, с большой осью, касательной к траектории в центре. Пористость и толщина, которые также участвуют в распределении растворенного вещества, интерполируются из соответствующих растров в центре, без учета информации из соседних ячеек. Замедление, время, коэффициент распада, продольная дисперсность и доля дисперсности задаются пользователем в виде констант.

Дисперсность

Дисперсность – это параметр, управляющий дисперсией растворенного вещества через пористую среду; она задается в единицах длины. В модели Фильтрация в водоносном горизонте дисперсность используется для вычисления дисперсии 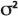в приведенном выше уравнении Гауссовой дисперсии, согласно:

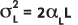• и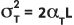
• 

Природа дисперсности и методы ее определения являются темами особого интереса и обсуждения среди специалистов, занимающихся моделированием подземного стока, и не существует никакой универсальной методики для определения этих значений. Обсуждение дисперсностей в различных геологических формациях можно найти в работе Gelhar и др. (1992).

Ни следующей диаграмме обобщается разнообразие данных, приведенных в опубликованных работах, и продольную дисперсность связывается с масштабом интересующей проблемы, то есть с расстоянием от источника до точки наблюдения.

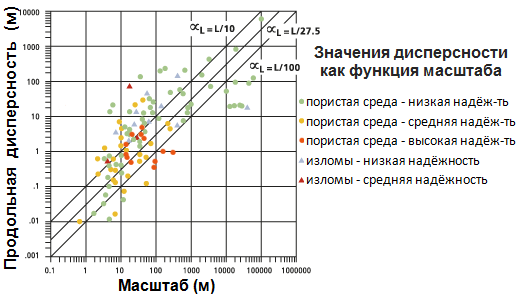
• Сплошная линия (центральная линия) на диаграмме представляет значение по умолчанию для продольной дисперсности, вычисленной инструментом Фильтрация в водоносном горизонте.

  Линия создается из приближения линейной регрессии 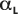к L что приводит к 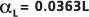или 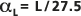, где длина пути перемещения L является шкалой наблюдений.

  Также показана статистика этой регрессии. Пунктирные внешние линии показаны 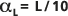и 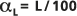для сравнения.

Такое используемое по умолчанию вычисление должно использоваться только как руководство к действию, поскольку некоторые исследователи отвергают применение такого универсального подхода. Для любого конкретного масштаба или места действительные значения дисперсностей могут находиться в диапазоне, превышающем два порядка от величины скорости потока, при этом более достоверные оценки указывают на более низкие значения. Вместо того чтобы использовать значение, предлагаемое по умолчанию, для которого нет никакой теоретической основы, вы должны провести несколько модельных экспериментов с использованием целого ряда значений дисперсности. Учет набора результатов более достоверен, чем работа с данными одного модельного эксперимента.

Аналогичные предостережения относятся к оценке отношения продольной дисперсности к поперечной, представленных на следующем рисунке. Эти значения, как правило, связаны с простыми отношениями, хотя опять таки, вы должны экспериментировать с диапазоном значений.

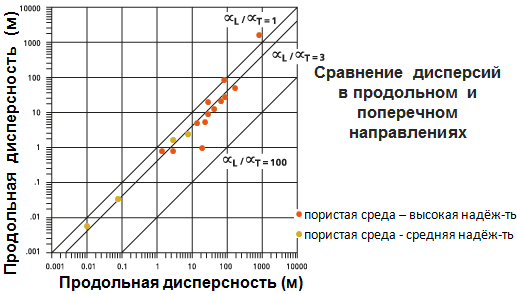
Доля дисперсности по умолчанию 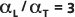указывается сплошной линией (центральная линия) на приведенном ниже рисунке. Пунктирные линии (внешние линии) показаны для 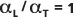и 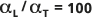для сравнения.

Гелхар (Gelhar, 1992) включает в сводные таблицы значения эффективной пористости и проницаемости формации. Таблицы с этими значениями можно найти в работах Freeze and Cherry (1979) и Marsily (1986).

Замедление потока

Замедление – это соотношение между скоростью транспортируемой жидкости и скоростью раствора, которое выражается безразмерной величиной в диапазоне от единицы до бесконечности. Коэффициент замедления, равный двум, означает, что раствор мигрирует через пористую среду со скоростью, вдвое меньше скорости просачивания. Идеальный изоиндикатор не претерпевает адсорбции и перемещается в растворе с жидкостью. Такой раствор имеет коэффициент замедления, равный единице, который означает, что он движется с той же скоростью, что и транспортирующая жидкость.

Это явление является результатом адсорбции и десорбции растворенного вещества в пористой среде, в особенности, органическими включениями на стенках пор. Уравнение замедления представлено в работе Freeze and Cherry (1979) следующим образом:

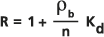
• , где:

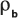  : Насыпная плотность материала.

  n : Пористость формации.

  K_d : Коэффициент распределения, который представляет декомпозицию раствора благодаря быстрой, обратимой адсорбции растворенного вещества между жидкой и твердыми фазами, предполагающей линейную изотерму.

В работе Marsily (1986) также подробно обсуждаются фактор замедления и адсорбция.

Выполнение моделирования адвекции-дисперсии

Инструменты Сток по Дарси, Трек частиц и Фильтрация в водоносном горизонте могут быть использованы для выполнения элементарного моделирования адвекции-дисперсии растворенных веществ в грунтовых водах. Сток по Дарси создает поле скорости потока грунтовых вод из геологических данных, Трек частиц идет по пути переноса через поле потока из точечного источника, а Фильтрация в водоносном горизонте вычисляет гидродинамическую дисперсию одновременного выпуска точки составляющего компонента, т.к. он переносится вдоль потока.

Подробно адвективно-дисперсионное моделирование, использующее эти инструменты, представлено в работе Tauxe (1994).

Типичная последовательность при выполнении моделирования подземного стока – запуск инструмента Сток по Дарси, , затем инструмента Трек частиц и, наконец, Фильтрация в водоносном горизонте.

Пример:

• Пример диалогового окна для инструмента Фильтрация в водоносном горизонте:

  Входной файл трека частиц : ttrack.txt

  Входной растр эффективной пористости : poros

  Входной растр толщины водоносного пласта : thickn

  Выходной растр : ppuff1

  Масса : 3,2e7

  Время дисперсии : 50000

  Продольная дисперсность : 6

  Доля дисперсности : 3

  Фактор замедления : 1

  Коэффициент затухания : 250

• Пример использования инструмента Фильтрация в водоносном горизонте в алгебре карт:

  outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
  

• Ниже приведена последовательность выражений алгебры карт, использующих инструменты моделирования подземного стока:

  out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1)
  ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp)
  out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
  

Литература

Bear, J. 1979, Hydraulics of Groundwater. McGraw–Hill.

Freeze, R. A., and J. A. Cherry. 1979. Грунтовые воды. Prentice–Hall.

Gelhar, L. W., C. Welty, and K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955–1974.

Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.

Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., University of Texas, Austin.